Dane są funkcje liniowe \(f(x)=x-2\) oraz \(g(x)=x+4\) określone dla wszystkich liczb rzeczywistych \(x\). Wskaż, który z poniższych wykresów jest wykresem funkcji \(h(x)=f(x)\cdot g(x)\).

Zgodnie z treścią zadania nasza funkcja \(h(x)\) jest iloczynem funkcji \(f(x)\) oraz \(g(x)\), zatem:
$$h(x)=f(x)\cdot g(x)=(x-2)\cdot(x+4)$$
Powyższy zapis jest już tak naprawdę wzorem naszej funkcji \(h(x)\) w postaci iloczynowej. Możemy też wymnożyć te wyrazy i zapisać wzór w postaci ogólnej, choć nie jest to konieczne:
$$h(x)=f(x)\cdot g(x)=(x-2)\cdot(x+4)=x^2+2x-8$$
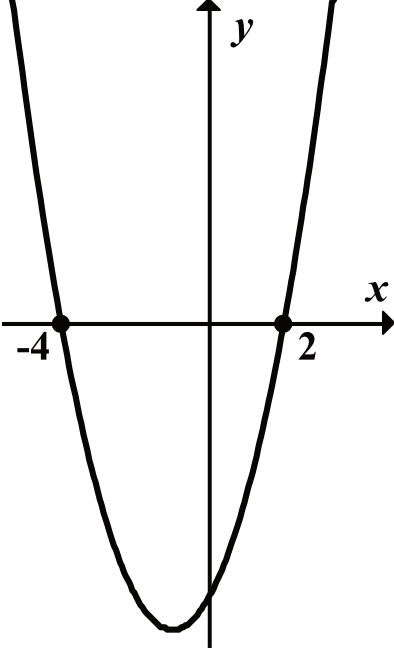
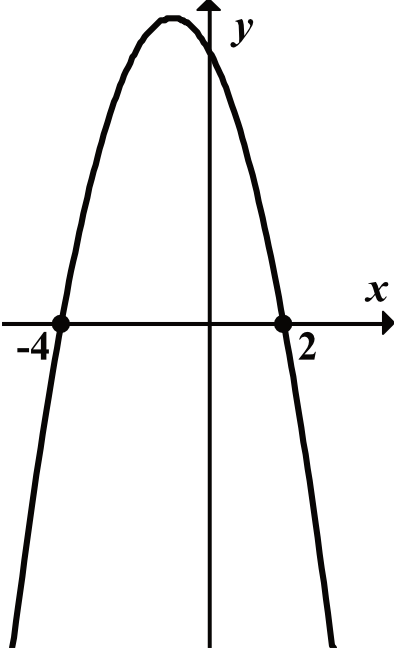
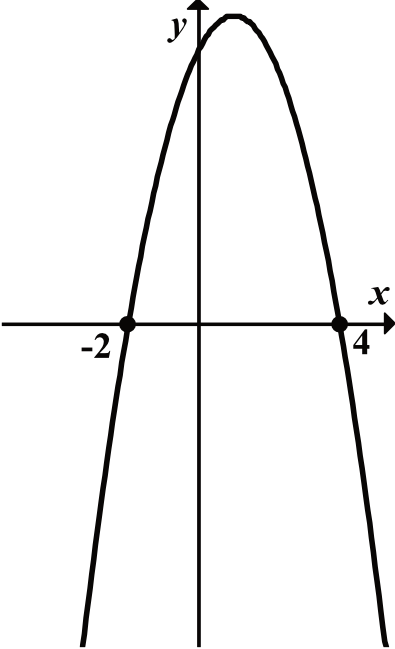
Dzięki postaci ogólnej wiemy już, że funkcja \(h(x)\) jest na pewno parabolą, której ramiona są skierowane do góry, bo współczynnik \(a\) stojący przed \(x^2\) jest dodatni.
Choć w pierwszym kroku zapisaliśmy wzór funkcji \(h(x)\) w postaci ogólnej i śmiało moglibyśmy z niej obliczyć miejsca zerowe za pomocą delty, to jednak łatwiej będzie skorzystać z postaci iloczynowej, czyli ze wzoru \(h(x)=(x-2)(x+4)\). Wystarczy teraz przyrównać wartości w nawiasach do zera, a więc:
$$x-2=0 \quad\lor\quad x+4=0 \\
x=2 \quad\lor\quad x=-4$$
Wiemy, że nasza parabola ma ramiona skierowane ku górze, że jej miejscami zerowymi są \(x=2\) oraz \(x=-4\), a więc bez żadnych wątpliwości jesteśmy w stanie stwierdzić, że poszukiwanym wykresem jest ten z pierwszej odpowiedzi.



A dlaczego raniona ku górze?
ponieważ, a wychodzi nam dodatnie. Jakby wyszło ujemne to ramiona byłyby do dołu
a skąd wiemy że jest dodatnie
Bo wzór naszej funkcji h(x) to x^2+2x-8, czyli współczynnik a=1, czyli jest dodatni :)