Dane są dwa okręgi: okrąg o środku w punkcie O i promieniu 5 oraz okrąg o środku w punkcie P i promieniu 3

Krok 1. Dostrzeżenie podobieństwa trójkątów.
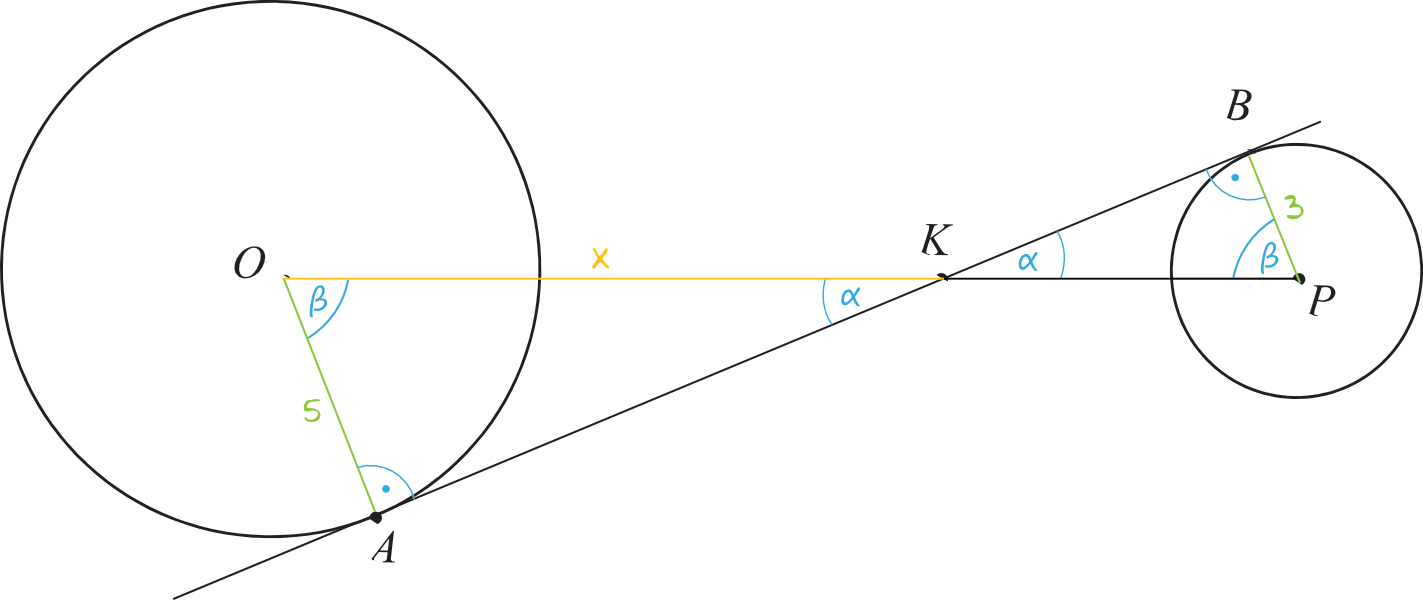
Spójrzmy na trójkąty \(OAK\) oraz \(BPK\). Są to trójkąty podobne i jesteśmy w stanie stwierdzić to na podstawie cechy kąt-kąt-kąt. W jaki sposób?
Styczna tworzy z promieniem kąt prosty, zatem jeden i drugi trójkąt są prostokątne. Dodatkowo kąty \(AKO\) oraz \(BKP\) są kątami wierzchołkowymi, a zgodnie z własnościami takich kątów będą one miały jednakową miarę. Skoro więc dwa kąty w tych trójkątach mają jednakowe miary, to i trzeci kąt ma tą samą miarę. To oznacza, że na pewno będą to trójkąty podobne.



Krok 2. Zapisanie równania.
Skoro są to trójkąty podobne, to muszą mieć one jednakowe stosunki długości boków. Skoro interesuje nas poznanie odcinka \(OK\) (czyli tak naprawdę przeciwprostokątnej trójkąta \(OAK\)) i znamy długości boków \(OA\) oraz \(BP\), to możemy ułożyć następującą proporcję:
$$\frac{|OA|}{|OK|}=\frac{|BP|}{|KP|} \\
\frac{5}{|OK|}=\frac{3}{|KP|}$$

Krok 3. Wyznaczenie długości odcinka \(OK\).
Mnożąc na krzyż równanie otrzymane w drugim kroku otrzymamy informację, że:
$$5\cdot|KP|=3\cdot|OK| \\
|KP|=\frac{3}{5}\cdot|OK|$$

Z rysunku oraz z treści zadania wynika, że:
$$|OK|+|KP|=16$$

Podstawiając informację o tym, że \(|KP|=\frac{3}{5}\cdot|OK|\) otrzymamy:
$$|OK|+\frac{3}{5}\cdot|OK|=16 \\
1,6\cdot|OK|=16 \\
|OK|=10$$