Przed Tobą sprawdzian z matematyki, który sprawdzi Twoją wiedzę z działu: Okręgi wpisane i opisane na wielokątach. W teście znajduje się 10 zadań, a każde z nich jest warte 1 punkt. Całość powinna Ci zająć około 15 minut. Po zakończeniu sprawdzianu możesz przejrzeć swoje odpowiedzi wraz z pełnymi rozwiązaniami do zadań. Życzę powodzenia!
Zadanie 1. (1pkt) Mamy następujący zestaw figur:

Na ilu powyższych rysunkach mamy zaprezentowaną sytuację w której okrąg jest wpisany (w matematycznym sensie) w wielokąt?
Zadanie 2. (1pkt) Dany jest trójkąt różnoboczny \(ABC\). Chcemy narysować okrąg, który będzie opisany na tym trójkącie. Jak znaleźć środek tego okręgu?
Zadanie 3. (1pkt) Na trójkącie prostokątnym o bokach \(\sqrt{3}, \sqrt{5}\) oraz \(\sqrt{8}\) został opisany okrąg. Promień tego okręgu ma długość:
Zadanie 4. (1pkt) 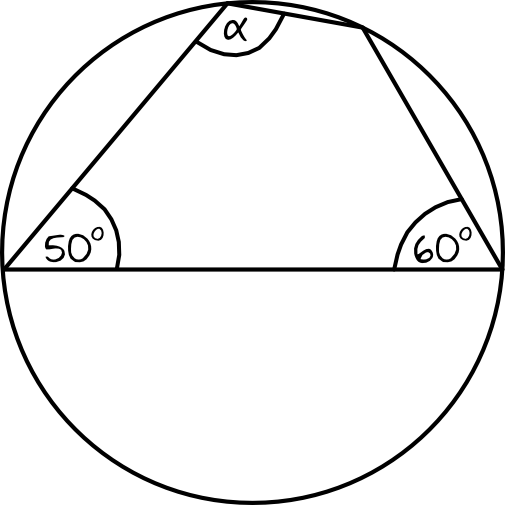
Kąt \(α\) ma miarę:
Zadanie 5. (1pkt) Z wielokątami opartymi na okręgach jest związana ciekawa własność. Okazuje się, że pole dowolnego wielokąta (np. czworokąta) opisanego na okręgu można obliczyć ze wzoru:
$$P=\frac{1}{2}r\cdot(a+b+c+d)$$
gdzie:
\(r\) - długość promienia okręgu
\(a,b,c,d\) - długości boku wielokąta
Jakie jest pole powierzchni czworokąta, którego obwód jest równy \(30\) i który jest opisany na okręgu o długości \(8π\)?
Zadanie 6. (1pkt) Na każdym trójkącie można opisać okrąg i w każdy trójkąt można wpisać okrąg.
Zadanie 7. (1pkt) Jeżeli okrąg jest wpisany w kwadrat o boku \(a\), to jego promień ma długość \(\frac{1}{2}a\).
Zadanie 8. (1pkt) Dany jest trójkąt równoramienny w którym wpisany jest okrąg. Jaś twierdzi, że w takiej sytuacji długość promienia okręgu jest równa \(\frac{2}{3}\) wysokości trójkąta. Małgosia uważa, że reguła podana przez Jasia jest błędna. Kto ma rację?
Zadanie 9. (1pkt) Pole trójkąta równobocznego wpisanego w okrąg o promieniu \(4\) jest równe:
Zadanie 10. (1pkt) Dany jest równoległobok \(ABCD\) w którym punkty \(A=(2;1)\) oraz \(B=(7;2)\) tworzą dłuższy bok tej figury. Punkt \(S=(5;3)\) jest środkiem symetrii tego równoległoboku. Jeżeli punkt \(D\) tworzy z punktem \(A\) krótszy bok równoległoboku to:
