Przed Tobą sprawdzian z matematyki, który sprawdzi Twoją wiedzę z działu: Kąt środkowy i wpisany. W teście znajduje się 10 zadań, a każde z nich jest warte 1 punkt. Całość powinna Ci zająć około 15 minut. Po zakończeniu sprawdzianu możesz przejrzeć swoje odpowiedzi wraz z pełnymi rozwiązaniami do zadań. Życzę powodzenia!
Zadanie 1. (1pkt) 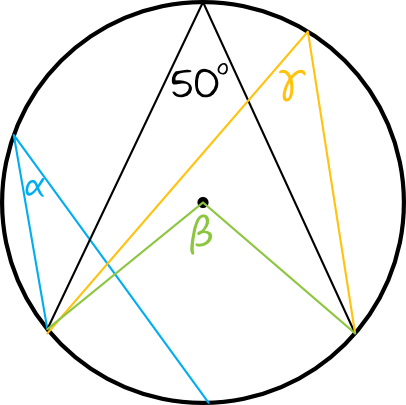
Na powyższym rysunku mamy zaznaczone trzy kąty: \(α, β, γ\). Ile z tych trzech kątów ma miarę \(50°\)?
Zadanie 2. (1pkt) 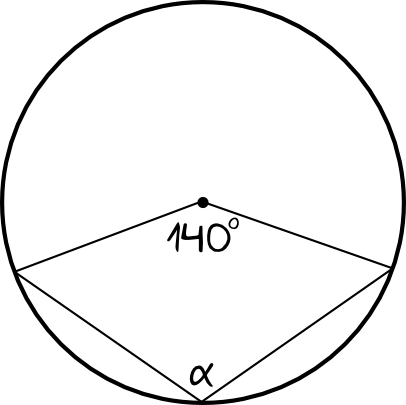
Kąt \(α\) ma miarę:
Zadanie 3. (1pkt) 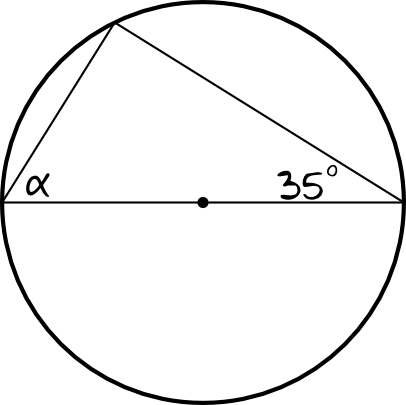
Kąt \(α\) zaznaczony na powyższym rysunku ma miarę:
Zadanie 4. (1pkt) 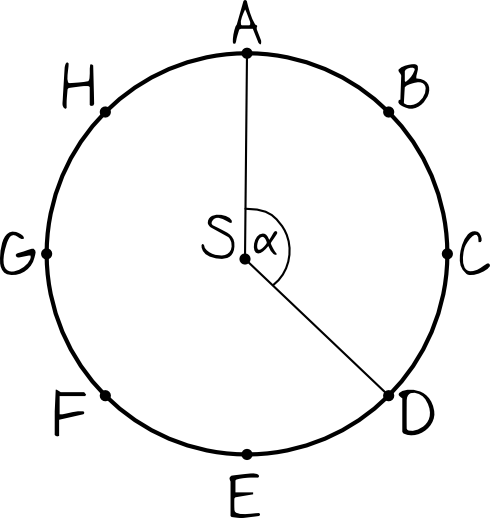
Punkty \(A-H\) dzielą okrąg na osiem równych łuków. W związku z tym kąt \(ASD\) ma miarę:
Zadanie 5. (1pkt) Kąty \(α\) i \(β\) są oparte na tym samym łuku, przy czym \(α\) to kąt środkowy, a \(β\) to kąt wpisany. Jeżeli \(α+β=180°\), to:
Zadanie 6. (1pkt) 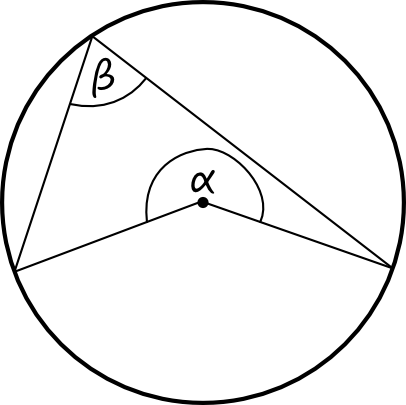
Na powyższym rysunku miara kąta \(α\) jest dwukrotnie większa od miary kąta \(β\).
Zadanie 7. (1pkt) 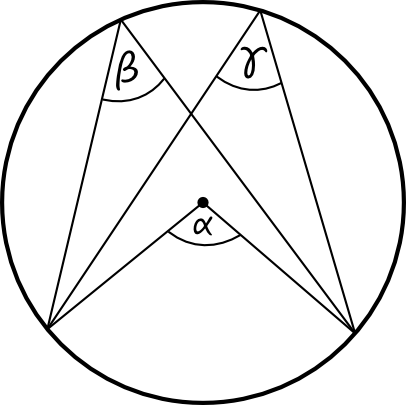
Zgodnie z oznaczeniami na powyższym rysunku możemy zapisać, że \(α=β+γ\).
Zadanie 8. (1pkt) 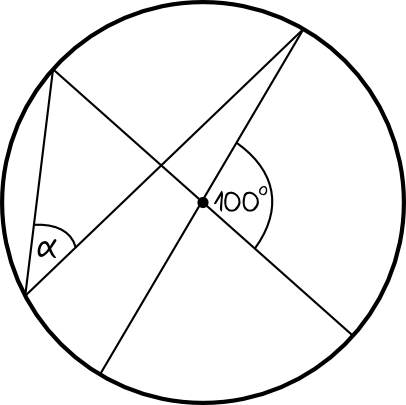
Jaś twierdzi, że kąt \(α\) zaznaczony na powyższym rysunku ma miarę \(50°\). Małgosia uważa, że miara tego kąta jest mniejsza. Kto ma rację?
Zadanie 9. (1pkt) 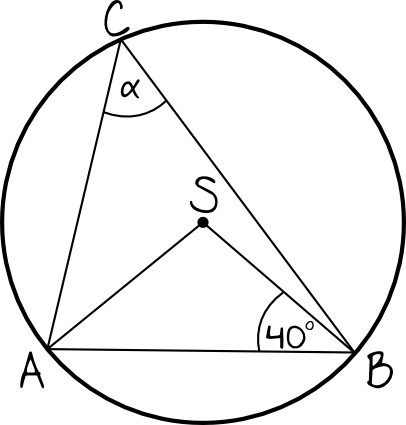
Kąt \(α\) zaznaczony na powyższym rysunku ma miarę:
Zadanie 10. (1pkt) Na okręgu o promieniu \(6\) zaznaczone są punkty \(A\) oraz \(B\), które tworzą łuk \(AB\). Na tym łuku oparty jest kąt środkowy o mierze \(120°\). Długość łuku jest równa:
