Przed Tobą sprawdzian z matematyki, który sprawdzi Twoją wiedzę z działu: Zależności między funkcjami trygonometrycznymi. W teście znajduje się 10 zadań, a każde z nich jest warte 1 punkt. Całość powinna Ci zająć około 15 minut. Po zakończeniu sprawdzianu możesz przejrzeć swoje odpowiedzi wraz z pełnymi rozwiązaniami do zadań. Życzę powodzenia!
Zadanie 1. (1pkt) Jeżeli \(α\) jest kątem ostrym i \(cosα=\frac{\sqrt{5}}{3}\), to:
Zadanie 2. (1pkt) \(sin150°=\)
Zadanie 3. (1pkt) Z jedynki trygonometrycznej wynika, że:
Zadanie 4. (1pkt) \((sinα+cosα)^2+(sinα-cosα)^2=\)
Zadanie 5. (1pkt) 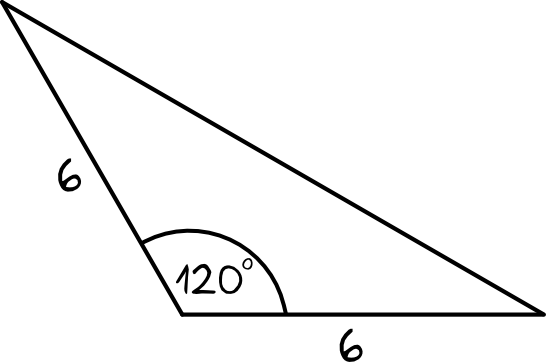
Pole powierzchni powyższego trójkąta jest równe:
Zadanie 6. (1pkt) Wartość wyrażenia \(\sqrt{\frac{sin50°}{cos40°}}\) jest mniejsza od \(1\).
Zadanie 7. (1pkt) Dla kątów rozwartych sinus przyjmuje wartości dodatnie, a cosinus przyjmuje wartości ujemne.
Zadanie 8. (1pkt) Wiemy, że sinus pewnego kąta ostrego jest równy \(\frac{7}{25}\), a cosinus jest równy \(\frac{24}{25}\). Jaś twierdzi, że w takim razie tangens tego kąta będzie równy \(\frac{24}{7}\). Małgosia uważa, że w takiej sytuacji tangens jest równy \(\frac{7}{24}\). Kto ma rację?
Zadanie 9. (1pkt) Jeżeli \(α\) jest kątem ostrym i \(tgα=3\), to:
Zadanie 10. (1pkt) Jakie jest pole równoległoboku o bokach \(5\) oraz \(8\), jeżeli kąt ostry ma miarę \(32°\)?
