Próbny egzamin ósmoklasisty z matematyki - CKE 2018
Arkusz zawiera 15 zadań zamkniętych oraz 6 zadań otwartych. Łącznie do zdobycia jest 30 punktów, a sugerowany maksymalny czas rozwiązywania to około 100 minut.
W przypadku zadań zamkniętych musisz zaznaczyć daną odpowiedź klikając w odpowiedni przycisk. Zadania otwarte rozwiąż na kartce papieru, a następnie przydziel sobie za nie odpowiednią liczbę punktów zgodnie z punktacją, która wyświetli się na ekranie. Zadania otwarte mają dodatkowo możliwość podejrzenia proponowanego rozwiązania, tak aby móc jak najrzetelniej przyznać sobie punkty za zadanie.
Jeżeli nie masz pewności jak rozwiązać dane zadanie, to możesz je opuścić i wrócić niego w dowolnej chwili. Kiedy uzupełnisz wszystkie zadania kliknij w przycisk zakończ. Na ekranie pojawi Ci się wtedy liczba zdobytych punktów oraz będziesz mieć możliwość przejrzenia swoich odpowiedzi wraz z pełnymi rozwiązaniami krok po kroku. Jeżeli jesteś gotowy/a to możesz przejść do pierwszego zadania.
Zadanie 1. (1pkt) Firma przesyłkowa korzysta z paczkomatów do samodzielnego nadawania i odbierania przesyłek przez klientów. Maksymalne wymiary prostopadłościennej paczki, którą można nadać za pośrednictwem tej firmy, wynoszą \(38cm\times41cm\times64cm\), a masa przesyłki nie może być większa niż \(25\) kg. W tabeli zapisano wymiary i masę czterech paczek.
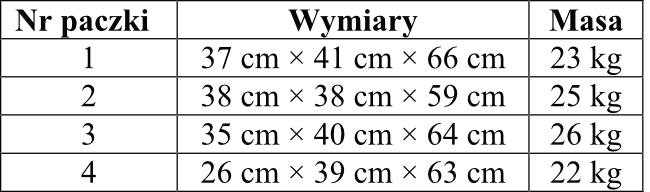
Które z tych paczek mogą być nadane przez paczkomat tej firmy?
Zadanie 2. (1pkt) Poniżej zamieszczono fragment etykiety z jogurtu o masie \(150g\).
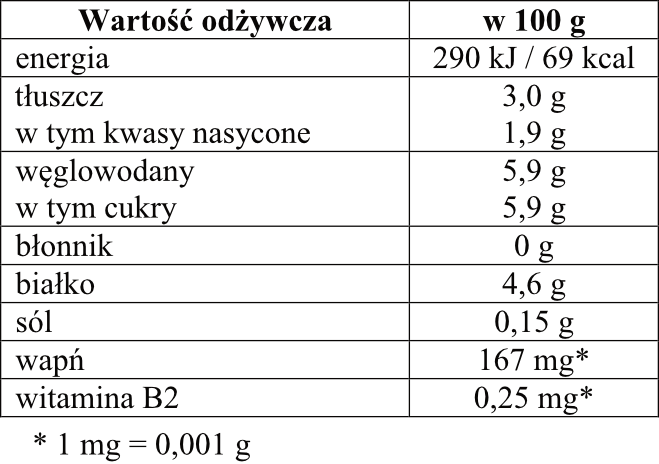
Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Zjedzenie całego jogurtu dostarcza organizmowi około \(\bbox[5px,border:1px solid]{A}\bigg/\bbox[5px,border:1px solid]{B}\) wapnia.
Zjedzenie całego jogurtu dostarcza organizmowi \(\bbox[5px,border:1px solid]{C}\bigg/\bbox[5px,border:1px solid]{D}\) razy więcej białka niż witaminy B2.
Zadanie 3. (1pkt) Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
\(120\%\) liczby \(180\) to tyle samo, co \(180\%\) liczby \(120\).
\(20\%\) liczby \(36\) to tyle samo, co \(40\%\) liczby \(18\).
Zadanie 4. (1pkt) Liczba \(x\) jest najmniejszą liczbą dodatnią podzielną przez \(3\) i \(4\), a liczba \(y\) jest największą liczbą dwucyfrową podzielną przez \(2\) i \(9\). Najmniejsza wspólna wielokrotność liczb \(x\) i \(y\) jest równa:
Zadanie 5. (1pkt) Na rysunku przedstawiono fragment podłogi pokrytej kaflami w kształcie kwadratów o boku długości \(60cm\) i kaflami w kształcie jednakowych prostokątów (patrz rysunek I). Na podłodze tej położono prostokątny dywan (patrz rysunek II).
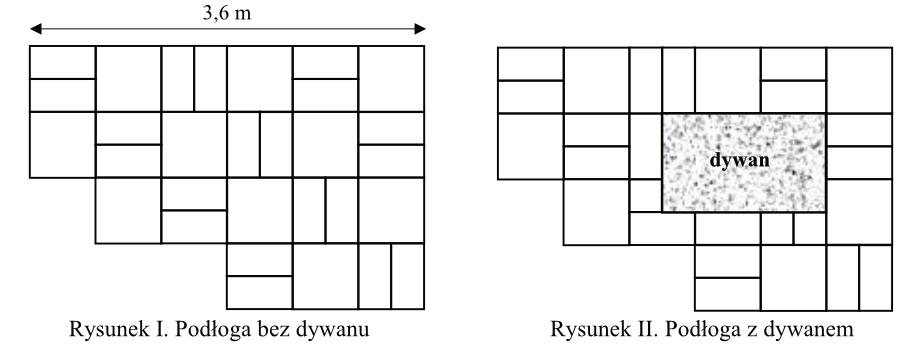
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Dywan ma powierzchnię większą niż powierzchnia \(4\) kwadratowych kafli.
Dywan ma wymiary \(90cm\times120cm\).
Zadanie 6. (1pkt) Prędkość rozchodzenia się impulsu elektrycznego u człowieka wynosi około \(2\) metrów na sekundę. U roślin impuls elektryczny może rozchodzić się z prędkością około \(60\) centymetrów na minutę. Ile razy prędkość rozchodzenia się impulsu elektrycznego u człowieka jest większa od prędkości rozchodzenia się impulsu elektrycznego u roślin?
Zadanie 7. (1pkt) Monika poprawnie zaokrągliła liczbę \(3465\) do pełnych setek i otrzymała liczbę \(x\), a Paweł poprawnie zaokrąglił liczbę \(3495\) do pełnych tysięcy i otrzymał liczbę \(y\). Czy liczby \(x\) i \(y\) są równe?
Wybierz odpowiedź A (Tak) albo B (Nie) i jej uzasadnienie spośród 1, 2 albo 3.
Zadanie 8. (1pkt) Dana jest liczba \(a=3\sqrt{2}-4\).
Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Liczba o \(2\) większa od liczby \(a\) jest równa \(\bbox[5px,border:1px solid]{A}\bigg/\bbox[5px,border:1px solid]{B}\):
Liczba \(2\) razy większa od liczby \(a\) jest równa \(\bbox[5px,border:1px solid]{C}\bigg/\bbox[5px,border:1px solid]{D}\):
Zadanie 9. (1pkt) Państwo Nowakowie mają trzy córki i jednego syna. Średnia wieku wszystkich dzieci państwa Nowaków jest równa \(10\) lat, a średnia wieku wszystkich córek jest równa \(8\) lat. Ile lat ma syn państwa Nowaków?
Zadanie 10. (1pkt) Do gry planszowej używane są dwa bączki o kształtach przedstawionych na rysunkach. Każdy bączek po zatrzymaniu na jednym boku wielokąta wskazuje liczbę umieszczoną na jego tarczy. Na rysunku \(I\) bączek ma kształt pięciokąta foremnego z zaznaczonymi liczbami od \(1\) do \(5\). Na rysunku \(II\) bączek ma kształt sześciokąta foremnego z zaznaczonymi liczbami od \(1\) do \(6\).
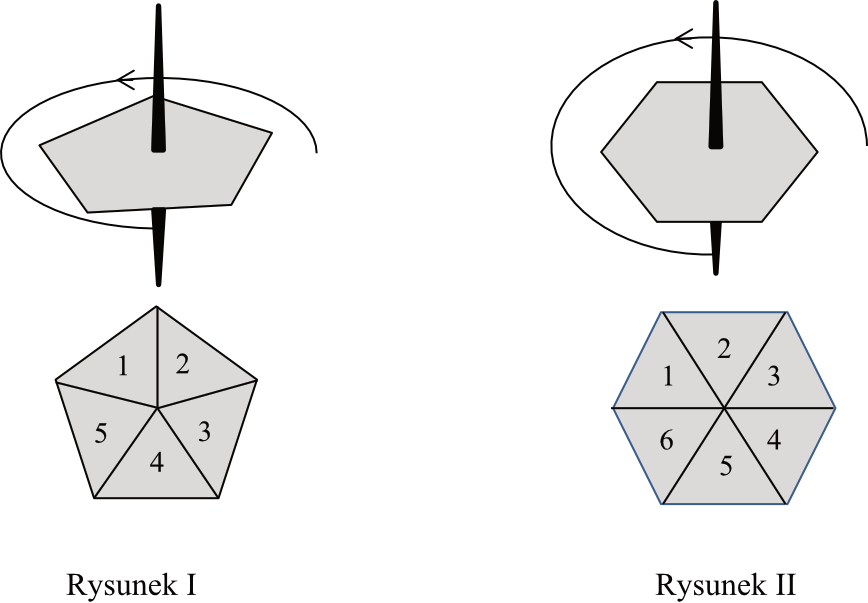
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Prawdopodobieństwo otrzymania liczby większej niż \(3\) na bączku z rysunku \(I\) jest większe niż \(\frac{1}{2}\).
Uzyskanie nieparzystej liczby na bączku z rysunku \(I\) jest tak samo prawdopodobne, jak uzyskanie nieparzystej liczby na bączku z rysunku \(II\).
Zadanie 11. (1pkt) O liczbie \(x\) wiemy, że \(\frac{1}{3}\) tej liczby jest o \(\frac{3}{4}\) większa od \(\frac{1}{6}\) tej liczby. Które równanie pozwoli wyznaczyć liczbę \(x\)?
Zadanie 12. (1pkt) W trójkącie \(ABC\) największą miarę ma kąt przy wierzchołku \(C\). Miara kąta przy wierzchołku \(A\) jest równa \(48°\), a miara kąta przy wierzchołku \(B\) jest równa różnicy miary kąta przy wierzchołku \(C\) oraz miary kąta przy wierzchołku \(A\).
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Kąt przy wierzchołku \(B\) ma miarę \(48°\).
Trójkąt \(ABC\) jest prostokątny.
Zadanie 13. (1pkt) W układzie współrzędnych zaznaczono dwa punkty: \(A=(-8,-4)\) i \(P=(-2, 2)\). Punkt \(P\) jest środkiem odcinka \(AB\). Jakie współrzędne ma punkt \(B\)?
Zadanie 14. (1pkt) Cztery jednakowe drewniane elementy, każdy w kształcie prostopadłościanu o wymiarach \(2cm\times2cm\times9cm\), przyklejono do metalowej płytki w sposób pokazany na rysunku \(I\).
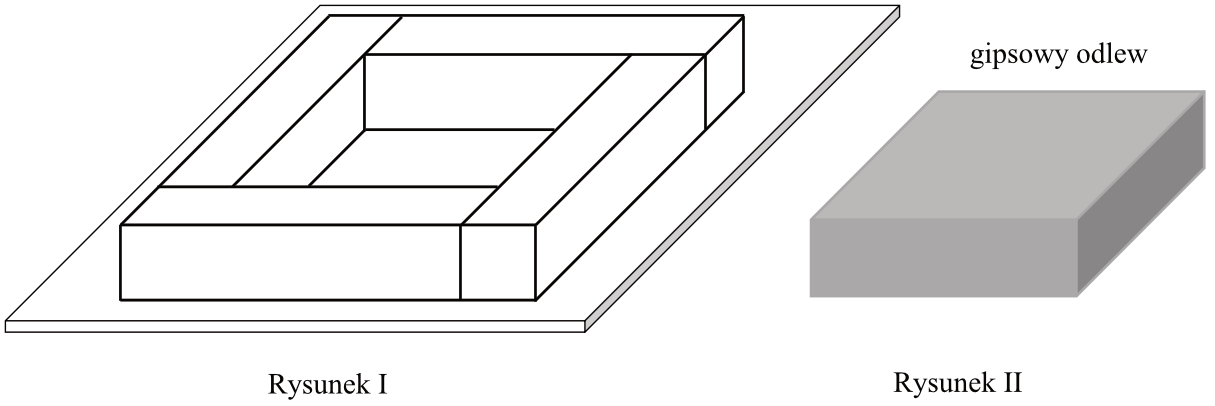
W ten sposób przygotowano formę, którą wypełniono masą gipsową, i tak otrzymano gipsowy odlew w kształcie prostopadłościanu, pokazany na rysunku \(II\).
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Objętość drewna, z którego zbudowano formę, jest równa \(\bbox[5px,border:1px solid]{A}\bigg/\bbox[5px,border:1px solid]{B}\):
Objętość gipsowego odlewu jest równa \(\bbox[5px,border:1px solid]{C}\bigg/\bbox[5px,border:1px solid]{D}\):
Zadanie 15. (1pkt) Na rysunkach przedstawiono ostrosłup prawidłowy i graniastosłup prawidłowy. Wszystkie krawędzie obu brył są jednakowej długości.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Suma długości wszystkich krawędzi ostrosłupa jest większa niż suma długości wszystkich krawędzi graniastosłupa.
Całkowite pole powierzchni ostrosłupa jest większe niż całkowite pole powierzchni graniastosłupa.
Zadanie 16. (2pkt) Prostokąt \(ABCD\) o wymiarach \(7\) cm i \(8\) cm rozcięto wzdłuż prostej \(a\) na dwa trapezy tak, jak pokazano na rysunku. Odcinek \(CL\) ma długość \(3,2cm\).
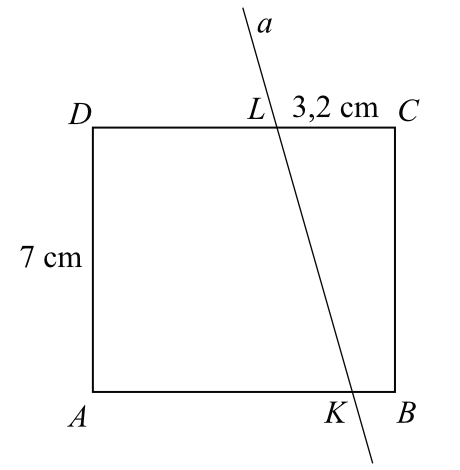
Pole trapezu \(KBCL\) jest czterokrotnie mniejsze od pola prostokąta \(ABCD\). Oblicz długość odcinka \(KB\). Zapisz obliczenia.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy zapiszesz równanie w którym jedyną niewiadomą jest długość boku \(KB\) (patrz: Krok 2.), ale samo równanie rozwiążesz błędnie.
ALBO
• Gdy obliczysz, że trapez \(KBCL\) ma mieć powierzchnię równą \(14cm^2\) oraz podstawisz dane do wzoru na pole trapezu otrzymując wyrażenie algebraiczne typu \(\frac{3,2cm+b}{2}\cdot7cm\), ale nie wpadniesz na pomysł, że trzeba z tych dwóch danych ułożyć równanie typu \(\frac{3,2cm+b}{2}\cdot7cm=14cm^2\).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Obliczenie pola powierzchni trapezu \(KBCL\).
Z treści zadania wynika, że prostokąt \(ABCD\) ma wymiary \(7cm\times8cm\). W związku z tym pole tego prostokąta jest równe:
$$P_{ABCD}=7cm\cdot8cm=56cm^2$$
Jeżeli pole trapezu jest czterokrotnie mniejsze od pola tego prostokąta, to znaczy że to pole jest równe:
$$P_{KBCL}=56cm^2:4=14cm^2$$
Krok 2. Obliczenie długości odcinka \(KB\).
O trapezie \(KBCL\) wiemy, że jedna z jego podstaw ma długość \(a=3,2cm\), wysokość ma miarę \(h=7cm\), a pole tego trapezu jest równe \(P=14cm^2\). W związku z tym jeżeli podstawę \(KB\) oznaczymy sobie symbolem \(b\), to korzystając ze wzoru na pole trapezu możemy zapisać, że:
$$P=\frac{a+b}{2}\cdot h \\
14cm^2=\frac{3,2cm+b}{2}\cdot7cm \quad\bigg/:7cm \\
2cm^2=\frac{3,2cm+b}{2} \quad\bigg/\cdot2 \\
4cm^2=3,2cm+b \\
b=0,8cm$$
To oznacza, że odcinek \(KB\) ma miarę \(0,8cm\).
Zadanie 17. (2pkt) Na pozalekcyjne zajęcia sportowe zapisanych jest \(37\) osób. Uzasadnij, że w tej grupie są co najmniej \(4\) osoby, które urodziły się w tym samym miesiącu.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy \(36\) osób rozdzielisz na poszczególne miesiące w taki sposób, że w każdym miesiącu są po \(3\) osoby i nie zapiszesz jakiegokolwiek wniosku końcowego.
ALBO
• Gdy \(36\) osób rozdzielisz na poszczególne miesiące w taki sposób, że w każdym miesiącu są po \(3\) osoby i przypiszesz trzydziestą siódmą osobę do konkretnego miesiąca (czyli np. założysz sztywno, że ta trzydziesta siódma osoba urodziła się w styczniu).
2 pkt
• Gdy przeprowadzisz pełne dowodzenie.
Wyjaśnienie:
Rok ma \(12\) miesięcy. Gdyby nawet w każdym miesiącu urodziły się dokładnie trzy osoby, to łącznie otrzymalibyśmy liczbę \(3\cdot12=36\) uczniów. Na zajęcia sportowe zapisanych jest \(37\) uczniów, a to oznacza, że ten trzydziesty siódmy uczeń musi być przynajmniej tym czwartym, który urodził się w danym miesiącu.
To oznacza, że w grupie \(37\) osób muszą być przynajmniej cztery osoby, które urodziły się w danym miesiącu. Gdyby grupa liczyła maksymalnie \(36\) osób, to takiej pewności już byśmy nie mieli.
Zadanie 18. (2pkt) Cztery jednakowe prostopadłościenne klocki, każdy o wymiarach \(2cm\times1cm\times1cm\), ułożono tak, jak przedstawiono na rysunku.
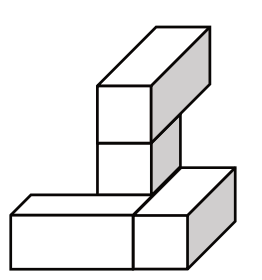
Następnie do tej budowli dołożono sześcienne klocki o krawędzi długości \(1\) cm tak, a by powstał prostopadłościan najmniejszy z możliwych. Uzupełnij zdania.
Liczba sześciennych klocków o krawędzi długości \(1\) cm, które należy dołożyć do budowli, jest równa ______.
Najmniejszy z możliwych prostopadłościanów, który w ten sposób otrzymano, ma wymiary ___ \(cm \times\) ___ \(cm \times\) ___ \(cm\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy poprawnie zapiszesz wymiary nowego prostopadłościanu (patrz: Krok 1.).
ALBO
• Gdy poprawnie obliczysz ile klocków sześciennych trzeba dołożyć (patrz: Krok 2.).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Ustalenie wymiarów prostopadłościanu.
Na początku spróbujmy ustalić jakie to wymiary będzie mieć nasz nowo powstały prostopadłościan. Najlepiej będzie to widać na rysunku pomocniczym:
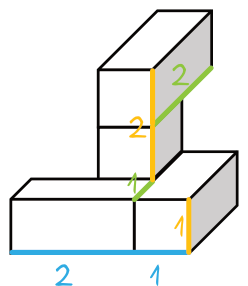
Po zsumowaniu odpowiednich długości widzimy wyraźnie, że nasz prostopadłościan będzie mieć wymiary \(3cm\times3cm\times3cm\).
Krok 2. Ustalenie ile klocków sześciennych trzeba dołożyć.
Nasz prostopadłościan będzie mieć wymiary \(3cm\times3cm\times3cm\), czyli jego objętość będzie równa:
$$V=3cm\cdot3cm\cdot3cm \\
V=27cm^3$$
W tym prostopadłościanie znajdują się już cztery klocki o wymiarach \(2cm\times1cm\times1cm\), czyli ich łączna objętość jest równa:
$$V=4\cdot2cm\cdot1cm\cdot1cm \\
V=4\cdot2cm^3 \\
V=8cm^3$$
To oznacza, że do zapełnienia kostkami sześciennymi zostaje nam przestrzeń równa \(27cm^3-8cm^3=19cm^3\).
Sześcienne kostki, które mamy dołożyć, mają długość krawędzi równą \(1cm\). W związku z tym objętość każdego takiego klocka jest równa:
$$V=1cm\cdot1cm\cdot1cm \\
V=1cm^3$$
W związku z tym liczba klocków sześciennych, które musimy dołożyć będzie równa:
$$19cm^3:1cm^3=19$$
Zadanie 19. (3pkt) Agata postanowiła przygotować kartkę okolicznościową w kształcie prostokąta, ozdobioną wzorem dokładnie takim, jak przedstawiony na rysunku. Kartka ta będzie miała wymiary \(15cm\times18cm\). Do jej ozdobienia Agata chce użyć jednakowych kwadratów, których bok wyraża się całkowitą liczbą centymetrów. Niektóre z tych kwadratów będzie musiała przeciąć na dwie lub na cztery jednakowe części.

Oblicz maksymalną długość boku jednego kwadratu. Do obliczeń przyjmij przybliżenie \(\sqrt{2}\approx1,4\). Zapisz obliczenia.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy przedstawisz poprawny sposób pozwalający na wyznaczenie długości boku kwadratu, korzystając z krótszego lub dłuższego boku (patrz: Krok 1. lub Krok 2.), ale samej długości nie wyznaczysz poprawnie (np. nie zaokrąglisz do \(3cm\), albo popełnisz błąd rachunkowy).
2 pkt
• Gdy przedstawisz poprawny sposób pozwalający na wyznaczenie długości boku kwadratu, korzystając z krótszego oraz dłuższego boku (patrz: Krok 1. oraz Krok 2.), ale samej długości nie wyznaczysz poprawnie (np. nie zaokrąglisz do \(3cm\), albo popełnisz błąd rachunkowy).
ALBO
• Gdy całe zadanie obliczysz poprawnie, ale do obliczeń wykorzystasz tylko jeden z boków kartki (patrz: Krok 1. oraz Krok 2.) i tym samym nie sprawdzisz, czy obliczone wymiary kwadratu pasują do drugiego boku prostokąta.
3 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Obliczenie maksymalnej długości boku kwadratu (licząc kwadraty na krótszym boku).
Z rysunku wynika, że wzdłuż boku kartki o długości \(15cm\) Agata zmieściła \(3\) kwadraty. Sprawdźmy zatem jaka może być maksymalna długość przekątnej takiego kwadratu (analizujemy przekątną, bo jest ona równoległa do boku kartki):
$$15cm:3=5cm$$
Z własności kwadratów wynika, że kwadrat o boku \(a\) ma przekątną o długości \(a\sqrt{2}\). Ta zależność pozwoli nam obliczyć długość boku kwadratu, przyjmując przybliżenie \(\sqrt{2}\approx1,4\):
$$a\sqrt{2}=5cm \\
1,4a\approx5cm \\
a\approx3,57cm$$
Z treści zadania wynika, że długość boku kwadratu musi wyrażać się całkowitą liczbą centymetrów, zatem największy możliwy kwadrat jaki zmieści się wzdłuż krótszej krawędzi kartki może mieć bok o długości \(3cm\).
Krok 2. Obliczenie maksymalnej długości boku kwadratu (licząc kwadraty na dłuższym boku).
To jednak nie koniec zadania, bo choć owszem wzdłuż krótszej krawędzi zmieszczą się trzy kwadraty o boku długości \(3cm\), to nie mamy jeszcze pewności, czy z takimi wymiarami zmieszczą się cztery kwadraty wzdłuż dłuższej krawędzi kartki. Musimy zatem wykonać podobne obliczenia dla dłuższego boku kartki.
Z rysunku wynika, że wzdłuż dłuższego boku kartki o długości \(18cm\) Agata zmieściła \(4\) kwadraty, zatem maksymalna długość przekątnej takiego kwadratu wynosi:
$$18cm:4=4,5cm$$
I tu ponownie korzystając z własności przekątnych obliczymy, że bok kwadratu może mieć długość:
$$a\sqrt{2}=4,5cm \\
1,4a\approx4,5cm \\
a\approx3,21cm$$
Zgodnie z treścią zadania bok kwadratu ma mieć całkowitą liczbę centymetrów, czyli wzdłuż dłuższego boku kartki także zmieści się nam kwadrat o boku długości \(3cm\).
To oznacza, że maksymalna długość boku kwadratu wynosi \(3cm\).
Zadanie 20. (3pkt) W wyborach na przewodniczącego klasy kandydowało troje uczniów: Jacek, Helena i Grzegorz. Każdy uczeń tej klasy oddał jeden ważny głos. Jacek otrzymał \(9\) głosów, co stanowiło \(36\%\) wszystkich głosów. Helena otrzymała o \(6\) głosów więcej niż Grzegorz. Oblicz, ile głosów otrzymała Helena, a ile - Grzegorz. Zapisz obliczenia.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy poprawnie obliczysz liczbę głosów oddanych w wyborach (patrz: Krok 1.) albo przynajmniej podasz poprawny sposób na wykonanie takiego obliczenia.
ALBO
• Gdy przedstawisz sposób na obliczenie łącznej liczby głosów oddanych na Helenę i Grzegorza (patrz: Krok 2.), ale otrzymany wynik będzie niepoprawny ze względu na jakieś błędy rachunkowe.
2 pkt
• Gdy przedstawisz poprawny sposób obliczenia głosów oddanych osobno na Helenę i Grzegorza (patrz: Krok 3.), ale otrzymany wynik będzie niepoprawny ze względu na jakieś błędy rachunkowe.
3 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Obliczenie liczby osób głosujących.
Na samym początku obliczmy ile osób głosowało w wyborach. Dokonamy tego dzięki informacji, która mówi o tym, że \(9\) zdobytych głosów stanowi \(36\%\) wszystkich głosów. Skoro tak, to możemy ułożyć następującą proporcję:
Skoro \(9\) głosów stanowi \(36\%\) wszystkich głosów
To \(1\) głos stanowi \(4\%\) wszystkich głosów
Więc \(25\) głosów stanowi \(100\%\) wszystkich głosów
To oznacza, że w głosowaniu oddano \(25\) głosów.
Krok 2. Obliczenie liczby głosów oddanych łącznie na Helenę oraz Grzegorza.
Skoro na Jacka oddano \(9\) głosów, a wszystkich głosów było \(25\), to na Grzegorza i Helenę oddano łącznie \(25-9=16\) głosów.
Krok 3. Obliczenie liczby głosów oddanych oddzielnie na Helenę oraz Grzegorza.
Wprowadźmy sobie proste oznaczenia:
\(x\) - liczba głosów oddanych na Grzegorza
\(x+6\) - liczba głosów oddanych na Helenę
Wiemy też, że łącznie ta dwójka zebrała \(16\) głosów, zatem możemy ułożyć następujące równanie:
$$x+x+6=16 \\
2x+6=16 \\
2x=10 \\
x=5$$
Naszą niewiadomą \(x\) jest liczba głosów oddanych na Grzegorza, a to oznacza, że na Grzegorza oddano \(5\) głosów.
Musimy jeszcze policzyć liczbę głosów oddanych na Helenę, a skoro Helena zdobyła \(6\) głosów więcej od Grzegorza, to Helenę oddano \(5+6=11\) głosów.
Zadanie 21. (3pkt) Ania postanowiła pojechać autobusem do babci do miejscowości Sokółka. Z domu wyszła o godzinie \(8{:}00\), kilka minut czekała na przystanku, a następnie jechała autobusem. Do Sokółki dotarła o godzinie \(9{:}30\) i tam na przystanku spotkała się z babcią. Na wykresie w sposób uproszczony przedstawiono zależność prędkości, z jaką poruszała się Ania, od czasu.
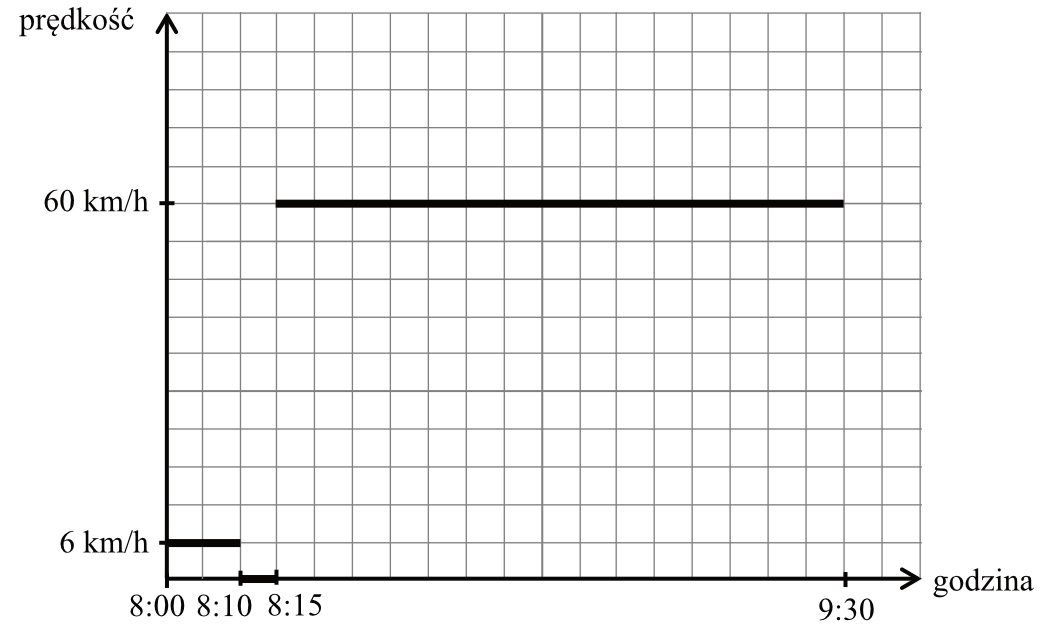
Oblicz długość trasy pokonanej przez Anię od wyjścia z domu do chwili spotkania z babcią. Zapisz obliczenia.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy zapiszesz poprawny sposób obliczenia długości trasy przebytej pieszo (patrz: Krok 2.), ale otrzymasz błędny wynik.
ALBO
• Gdy zapiszesz poprawny sposób obliczenia długości trasy przebytej autobusem (patrz: Krok 2.), ale otrzymasz błędny wynik.
2 pkt
• Gdy zapiszesz poprawny sposób obliczenia długości trasy przebytej pieszo oraz autobusem (patrz: Krok 2.), ale otrzymasz błędny wynik.
3 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Zapisanie kluczowych informacji z wykresu.
Musimy z podanego wykresu odczytać kluczowe informacje na temat czasu oraz prędkości poruszania się przez Anię. Wypisując te dane musimy pamiętać o tym, by ujednolicić sobie jednostki. Skoro prędkość mamy podaną w \(\frac{km}{h}\) to dobrze by było od razu zapisywać czas w przeliczeniu na godziny.
Trasę pokonaną przez Anię możemy podzielić na dwa etapy:
1. Pieszo z domu na przystanek (od godziny \(8{:}00\) do \(8{:}10\)):
Czas pokonania trasy: \(10\) minut, czyli \(t=\frac{1}{6}h\)
Prędkość: \(v=6\frac{km}{h}\)
2. Autobusem do babci (od godziny \(8{:}15\) do \(9{:}30\)):
Czas pokonania trasy: \(1\) godzina i \(15\) minut, czyli \(t=\frac{5}{4}h\)
Prędkość: \(v=60\frac{km}{h}\)
Czas oczekiwania na przystanku nie jest dla nas istotny, ponieważ w tym momencie Ania nie pokonywała żadnego dystansu.
Krok 2. Obliczenie długości pokonanej trasy.
Skorzystamy tutaj z klasycznego wzoru na prędkość \(v=\frac{s}{t}\). Przekształcając ten wzór otrzymamy wzór na drogę:
$$v=\frac{s}{t} \quad\bigg/\cdot t \\
s=vt$$
Teraz możemy obliczyć długości poszczególnych tras:
1. Pieszo z domu na przystanek:
$$s=vt \\
s=6\frac{km}{h}\cdot\frac{1}{6}h \\
s=1km$$
2. Autobusem do babci:
$$s=vt \\
s=60\frac{km}{h}\cdot\frac{5}{4}h \\
s=\frac{300}{4}km \\
s=75km$$
To oznacza, że łącznie Ania pokonała \(1km+75km=76km\).