Matura próbna z matematyki (poziom podstawowy) - Nowa Era 2023
Łącznie do zdobycia jest 46 punktów, a sugerowany maksymalny czas rozwiązywania to 180 minut.
Zadanie 1. (1pkt) Wartość wyrażenia \(log_{4}2+log_{4}8+log_{4}16\) jest równa:
Zadanie 2. (1pkt) Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych. Liczba \(\sqrt[2]{2\cdot\sqrt[3]{2}}\) jest równa:
Zadanie 3. (1pkt) Dla dowolnych liczb rzeczywistych \(a\) i \(b\) wyrażenie \((2a-3b)^2-(3a+2b)^2\) jest równe:
Zadanie 4. (1pkt) Ile jest wszystkich dwucyfrowych liczb naturalnych większych od \(20\), w których zapisie dziesiętnym występują tylko cyfry parzyste?
Zadanie 5. (2pkt) Na rysunku przedstawiono geometryczną interpretację układu równań stopnia pierwszego z dwiema niewiadomymi \(x\) i \(y\). Punkt przecięcia dwu prostych oraz ich punkty wspólne z osią \(Ox\) układu współrzędnych mają współrzędne całkowite.

Dokończ zdanie. Wybierz dwie odpowiedzi, tak aby dla każdej z nich dokończenie poniższego zdania było prawdziwe.
Układem równań, którego interpretację geometryczną przedstawiono na rysunku powyżej, jest układ:
Zadanie 6. (1pkt) Dany jest wielomian \(W(x)=2(x-1)(x+3)(x^2+4)\). Iloczyn wszystkich rzeczywistych pierwiastków tego wielomianu jest równy:
Zadanie 7. (1pkt) Równanie \(\dfrac{(2x-4)(2x-6)^2}{(1-x)(2-x)}=0\) ma w zbiorze liczb rzeczywistych:
Zadanie 8. (1pkt) Równanie \(|x-3|=m\) z niewiadomą \(x\) ma dwa rozwiązania. Jednym z nich jest liczba \(5\). Drugim rozwiązaniem tego równania jest liczba:
Zadanie 9. (1pkt) Dla \(x=\dfrac{\sqrt{5}-2}{\sqrt{5}}\) wartość wyrażenia \(\dfrac{-2}{x-1}\) jest równa:
Zadanie 10. (2pkt) Wykaż, że dla każdej liczby naturalnej \(n\ge2\) liczba \(8^n-2^n\) jest podzielna przez \(12\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy doprowadzisz liczbę do postaci \(2n\cdot(2n−1)(2n+1)\) lub innej podobnej.
2 pkt
• Gdy przeprowadzisz pełne dowodzenie.
Wyjaśnienie:
Wyłączając wspólny czynnik przed nawias, możemy naszą liczbę rozpisać w następujący sposób:
$$8^n-2^n=2^{n}\cdot(4^{n}-1)$$
Teraz powinniśmy dostrzec, że wyrażenie w nawiasie da się rozpisać wykorzystując wzór skróconego mnożenia \(a^2-b^2=(a-b)(a+b)\). Dzięki temu otrzymamy taką oto sytuację:
$$2^{n}\cdot(2^{n}-1)\cdot(2^{n}+1)$$
Jeśli się dobrze przyjrzymy, to zauważymy, że liczby \(2^{n}-1\), \(2^{n}\) oraz \(2^{n}+1\) to po prostu trzy kolejne liczby naturalne. To z kolei prowadzi nas do wniosku, że jedna z tych liczb jest podzielna przez \(3\).
Dodatkowo z treści zadania wiemy, że \(n\ge2\), a to by oznaczało, że liczba \(2^n\) jest na pewno liczbą parzystą i to taką, która jest podzielna przez \(4\).
To oznacza, że nasza liczba jest podzielna przez \(3\) i przez \(4\) jednocześnie, więc jest tym samym podzielna przez \(12\), co należało udowodnić.
Zadanie 11. (5pkt) Na rysunku przedstawiono fragment paraboli, która jest wykresem funkcji kwadratowej \(f\). Ta parabola przecina oś \(Oy\) w punkcie \((0,2)\), a jej wierzchołkiem jest punkt \((1,4)\).

Zadanie 11.1. Wyznacz i zapisz równanie osi symetrii wykresu funkcji \(f\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Zadanie 11.2. Wyznacz wzór funkcji \(f\). Zapisz obliczenia.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Zadanie 11.3. Funkcja \(g\) jest określona dla każdej liczby rzeczywistej \(x\) wzorem \(g(x)=f(x)+m\), gdzie \(m\) jest pewną liczbą rzeczywistą. Jednym z miejsc zerowych funkcji \(g\) jest liczba \(0\). Liczba \(m\) jest równa:
Zadanie 12. (4pkt) Na rysunku przedstawiono fragment wykresu funkcji wykładniczej \(f\) określonej wzorem \(f(x)=a^x\) oraz leżący na tym wykresie punkt \(A=(2,3)\).
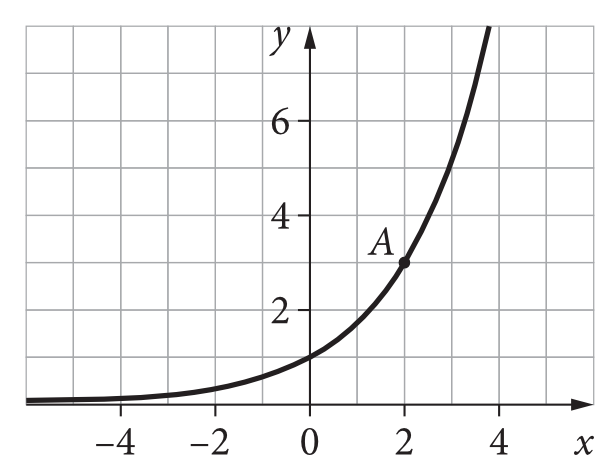
Zadanie 12.1. Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe.
Liczba \(f(0)-f(3)\) jest ujemna.
Liczba \(log_{3}f(2)\) jest równa \(1\).
Zadanie 12.2. Oblicz wartość \(a\). Zapisz obliczenia.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Zadanie 12.3. Jeden z poniższych rysunków przedstawia fragment wykresu funkcji \(g\) określonej wzorem \(g(x)=f(x-3)\). Fragment wykresu funkcji \(g\) przedstawiono na rysunku:
Zadanie 13. (1pkt) Dana jest prosta \(k\) o równaniu \(y=\frac{1}{3}x+4\). Prosta \(l\) o równaniu \(y=(2m+1)x-2\), gdzie \(m\) to pewna liczba rzeczywista, jest prostopadła do prostej \(k\).
Liczba \(m\) jest równa:
Zadanie 14. (1pkt) Na początku listopada w bufecie pracowniczym podniesiono cenę za obiad z \(20 zł\) do \(24 zł\). Z końcem miesiąca okazało się, że sprzedano mniej obiadów niż w październiku, ale wpływy z ich sprzedaży w listopadzie były o \(8\%\) wyższe niż w miesiącu przed podwyżką.
Liczba sprzedanych obiadów w listopadzie spadła o:
Zadanie 15. (1pkt) Dany jest ciąg \((a_{n})\) określony wzorem \(a_{n}=3\cdot(-2)^n\) dla każdej liczby naturalnej \(n\ge1\).
Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe.
Ciąg \((a_{n})\) jest ciągiem geometrycznym o ilorazie \(3\).
Ciąg \((a_{n})\) jest malejący.
Zadanie 16. (1pkt) Kąt \(\alpha\) jest ostry, a \(sin\alpha=2\cdot cos\alpha\).
Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe.
\(sin\alpha=\frac{1}{2}\)
Zadanie 17. (1pkt) Dany jest trójkąt \(ABC\), w którym \(2\cdot|AB|=3\cdot|BC|=4\cdot|AC|=12\).
Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe.
Obwód trójkąta \(ABC\) jest równy \(12\).
Trójkąt \(ABC\) jest ostrokątny.
Zadanie 18. (1pkt) Punkt \(A\) jest środkiem okręgu stycznego do obu osi układu współrzędnych i leży na prostej o równaniu \(y=-3x+8\). Obie współrzędne punktu \(A\) są dodatnie.
Promień omawianego okręgu jest równy:
Zadanie 19. (2pkt) Dany jest trójkąt \(ABC\), w którym \(|AC|=5\). Dwusieczna \(CD\) kąta \(ACB\) dzieli bok \(AB\) na odcinki o długości \(|AD|=4\), \(|DB|=3\) (zobacz rysunek).
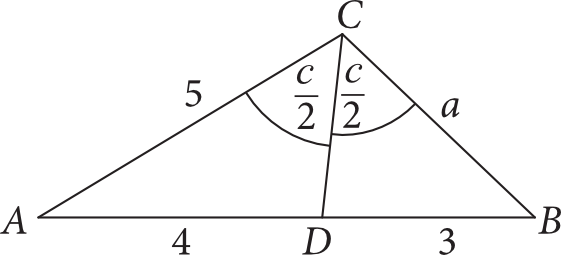
Oblicz długość \(a\) boku \(BC\) trójkąta \(ABC\). Zapisz obliczenia.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy poprawnie zapiszesz proporcję \(\frac{a}{3}=\frac{5}{4}\)
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
W tym zadaniu skorzystamy z twierdzenia o dwusiecznej kąta w trójkącie. Na jego podstawie możemy ułożyć następującą proporcję:
$$\frac{a}{3}=\frac{5}{4} \quad\bigg/\cdot3 \\
a=\frac{15}{4}$$
Zadanie 20. (1pkt) Punkty \(A=(1,1)\) i \(C=(5,5)\) są przeciwległymi wierzchołkami rombu \(ABCD\). Wierzchołek \(B\) leży na osi \(Ox\) układu współrzędnych.
Wierzchołek \(B\) ma współrzędne:
Zadanie 21. (1pkt) Na okręgu o środku \(S\) wybrano takie punkty: \(A\), \(B\) i \(C\), że \(|\sphericalangle ASB|=124°\), a \(|\sphericalangle BSC|=92°\) (zobacz rysunek).
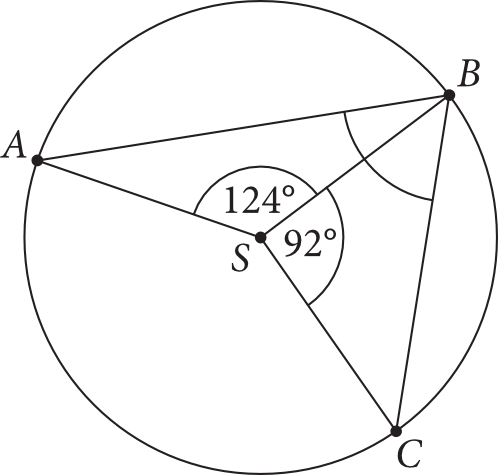
Miara kąta \(ABC\) jest równa:
Zadanie 22. (1pkt) Trójkąt \(ABC\) jest trójkątem równoramiennym, w którym \(|AC|=|BC|\). Punkt \(D\) jest środkiem podstawy \(AB\) trójkąta, a \(E\) – środkiem boku \(AC\). Półproste \(EF\) i \(AG\) przecinają odcinek \(CD\) w punktach \(F\) i \(G\) (jak na rysunku).
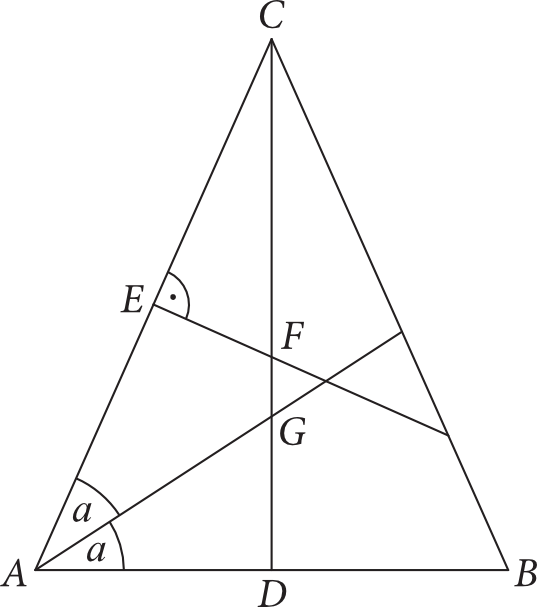
Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A albo B oraz jej uzasadnienie 1., 2. albo 3.
Środkiem okręgu wpisanego w trójkąt \(ABC\) jest punkt:
ponieważ jest on punktem przecięcia
Zadanie 23. (1pkt) Okrąg o środku \(S\) jest styczny do prostej \(k\) w punkcie \(A\). Punkt \(B\) leży na prostej \(k\) w odległości \(24\) od punktu \(A\) i w odległości \(26\) od punktu \(S\).
Promień tego okręgu jest równy:
Zadanie 24. (1pkt) W pewnym graniastosłupie prawidłowym czworokątnym przekątna ściany bocznej jest pięć razy dłuższa od przekątnej podstawy.
Stosunek długości krawędzi bocznej tego graniastosłupa do długości krawędzi jego podstawy jest równy:
Zadanie 25. (1pkt) Podstawą ostrosłupa prawidłowego trójkątnego \(ABCS\) jest trójkąt równoboczny \(ABC\). Pole ściany bocznej ostrosłupa jest dwa razy większe od pola jego podstawy. Wysokość \(SO\) tego ostrosłupa jest równa \(6\) (zobacz rysunek).
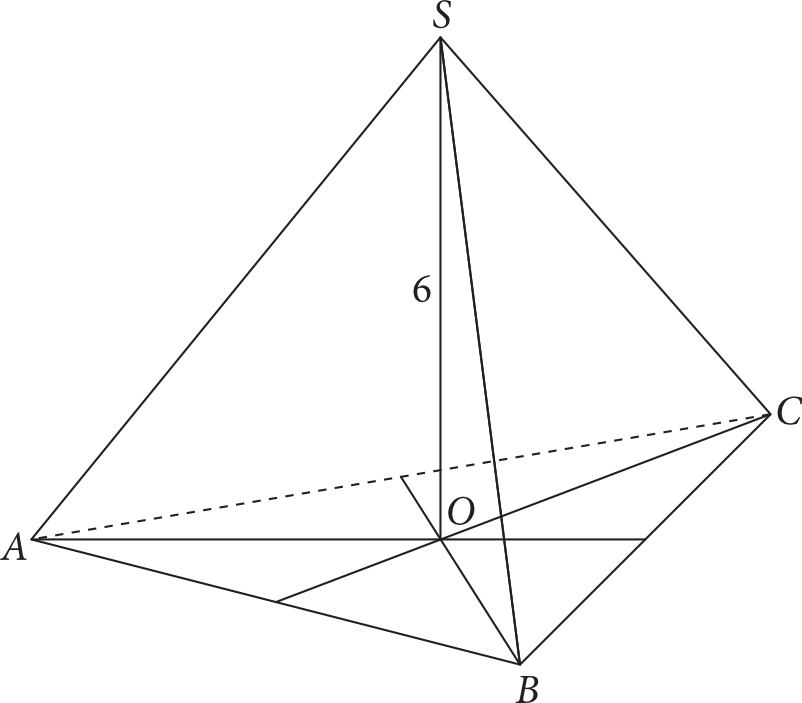
Wysokość ostrosłupa poprowadzona z wierzchołka \(C\) do ściany bocznej \(ABS\) jest równa:
Zadanie 26. (1pkt) W dwóch pudełkach umieszczono \(7\) kul. W jednym z pudełek znalazły się cztery kule ponumerowane liczbami: \(1\), \(2\), \(3\) i \(4\), a w drugim pudełku − trzy kule ponumerowane liczbami: \(2\), \(3\) i \(4\). Gra polega na losowaniu dwóch kul – po jednej z każdego pudełka, a kończy się wygraną, jeśli suma liczb z wylosowanych kul jest podzielna przez \(3\).
Prawdopodobieństwo wygranej w tej grze jest równe:
Zadanie 27. (3pkt) Ciąg arytmetyczny \((a_{n})\) ma dwanaście wyrazów, których suma jest równa \(168\). Różnica \(a_{1}-a_{12}\) wynosi \(22\).
Wyznacz wzór ogólny ciągu \((a_{n})\). Zapisz obliczenia.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy skorzystasz ze wzoru na sumę \(n\) początkowych wyrazów i zapiszesz równanie w którym są dwie niewiadome (patrz: Krok 1.).
2 pkt
• Gdy obliczysz \(a_{1}\) oraz \(a_{12}\) (patrz: Krok 1.).
ALBO
• Gdy zapiszesz poprawny układ równań z którego możemy obliczyć \(a_{1}\) oraz \(r\).
3 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Obliczenie wartości \(a_{1}\) oraz \(a_{12}\).
Korzystając ze wzoru na sumę \(n\) początkowych wyrazów ciągu, możemy zapisać, że:
$$S_{n}=\frac{a_{1}+a_{12}}{2}\cdot12 \\
168=\frac{a_{1}+a_{12}}{2}\cdot12 \\
14=\frac{a_{1}+a_{12}}{2} \\
a_{1}+a_{12}=28$$
Z treści zadania wiemy, że \(a_{1}-a_{12}=22\), czyli że tym samym \(a_{1}=22+a_{12}\). Podstawiając tę informację do równania \(a_{1}+a_{12}=28\), wyjdzie nam, że:
$$22+a_{12}+a_{12}=28 \\
2a_{12}=6 \\
a_{12}=3$$
Musimy jeszcze obliczyć wartość \(a_{1}\). Zapisaliśmy przed chwilą, że \(a_{1}=22+a_{12}\), zatem:
$$a_{1}=22+3 \\
a_{1}=25$$
Krok 2. Obliczenie różnicy ciągu.
Do wyznaczenia wzoru potrzebujemy jeszcze różnicy ciągu arytmetycznego. Korzystając ze wzoru na \(n\)-ty wyraz ciągu arytmetycznego wiemy, że:
$$a_{12}=a_{1}+11r$$
Podstawiając do tego równania znane nam \(a_{1}=25\) oraz \(a_{12}=3\), otrzymamy:
$$3=25+11r \\
11r=-22 \\
r=-2$$
Krok 3. Zapisanie wzoru.
Do zapisania wzoru skorzystamy ze standardowego wzoru na \(n\)-ty wyraz ciągu arytmetycznego:
$$a_{n}=a_{1}+(n-1)r$$
Podstawiając do niego \(a_{1}=25\) oraz \(r=-2\), otrzymamy:
$$a_{n}=25+(n-1)\cdot(-2) \\
a_{n}=25-2n+2 \\
a_{n}=-2n+27$$
Zadanie 28. (7pkt) Rozważamy wszystkie trójkąty prostokątne \(ABC\) o przeciwprostokątnej \(AC\), w których \(A=(0,0)\), \(B=(m,0)\), a wierzchołek \(C\) leży na prostej o równaniu \(y=-\frac{1}{2}x+5\) i obie jego współrzędne są liczbami dodatnimi. Na rysunku przedstawiono jeden z takich trójkątów.
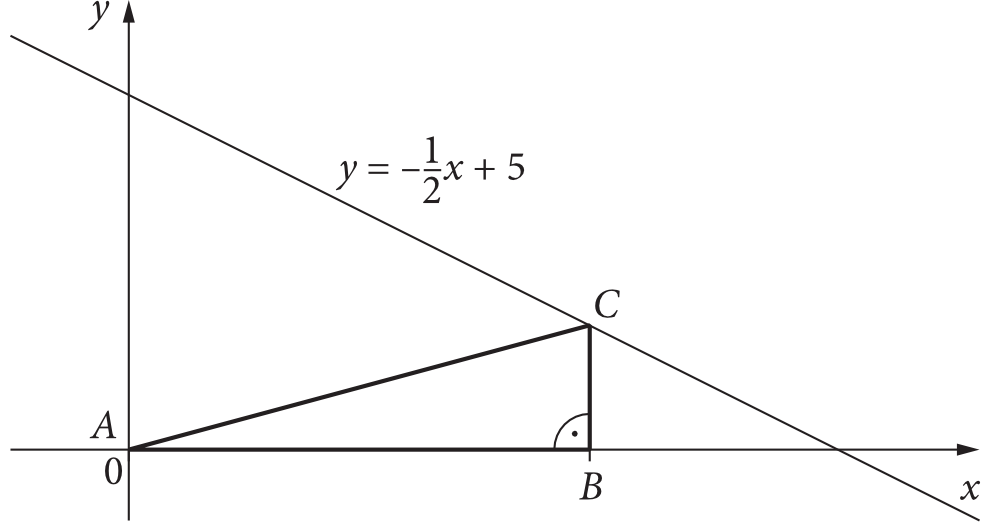
Zadanie 28.1. Wyznacz długość przeciwprostokątnej \(AC\) trójkąta – spośród rozważanych – w którym długość przyprostokątnej \(BC\) jest równa \(2\). Zapisz obliczenia.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Zadanie 28.2. Podaj wzór i dziedzinę funkcji opisującej zależność pola trójkąta \(ABC\) od \(m\). Oblicz współrzędne wierzchołka \(C\) tego spośród rozważanych trójkątów, który ma największe pole. Zapisz obliczenia.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy zapiszesz współrzędne punktu \(C\) w zależności od zmiennej \(m\) (patrz: Krok 1.).
ALBO
• Gdy zapiszesz, że \(m\gt0\) i \(m\lt10\).
2 pkt
• Gdy zapiszesz wzór na pole trójkąta w zależności od zmiennej \(m\) (patrz: Krok 2.).
3 pkt
• Gdy wyznaczysz współrzędne punktu \(C\) (patrz: Krok 5.), ale nie zapiszesz dziedziny (patrz: Krok 3.).
ALBO
• Gdy wyznaczysz \(x_{C{\) (patrz: Krok 4.) i zapiszesz dziedzinę (patrz: Krok 3.).
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Rozpisanie współrzędnych punktu \(C\).
Powinniśmy dostrzec, że współrzędna \(x_{C}\) musi być taka sama jak \(x_{B}\) (dobrze to było widać chociażby w poprzedniej części zadania). Skoro więc współrzędna \(x_{B}=m\) (tak wynika z treści zadania), to także \(x_{C}=m\). Dodatkowo, skoro punkt \(C\) leży na prostej określonej równaniem \(y=-\frac{1}{2}x+5\), to możemy zapisać, że \(y_{C}=-\frac{1}{2}m+5\).
To pozwala nam zapisać, że \(C=(m;-\frac{1}{2}m+5)\).
Krok 2. Zapisanie wzoru funkcji \(P(m)\).
Pole trójkąta \(ABC\) obliczymy ze wzoru:
$$P=\frac{1}{2}\cdot|AB|\cdot|BC|$$
Powinniśmy zauważyć, że długość odcinka \(AB\) będzie równa tyle, co współrzędna \(x\) punktu \(B\), czyli \(|AB|=m\). Z kolei wysokość \(|BC|\) będzie równa tyle, ile współrzędna \(y\) punktu \(C\), czyli \(|BC|=-\frac{1}{2}m+5\). Jeśli tego nie dostrzegasz, to zwróć uwagę na pierwsze zadanie, tam jest to bardzo dobrze widoczne.
Możemy więc zapisać, że:
$$P=\frac{1}{2}\cdot m\cdot(-\frac{1}{2}m+5) \\
P=-\frac{1}{4}m^2+\frac{5}{2}m$$
Otrzymaliśmy informację, że pole powierzchni można opisać wzorem \(-\frac{1}{4}m^2+\frac{5}{2}m\). W ten sposób udało nam się zapisać wzór na pole z użyciem tylko jednej niewiadomej. Teraz całość możemy potraktować jak funkcję kwadratową (dla jakiejś wartości \(m\) otrzymamy konkretne pole \(P\)). Zapisalibyśmy więc, że \(P(m)=-\frac{1}{4}m^2+\frac{5}{2}m\).
Krok 3. Wyznaczenie dziedziny funkcji.
Współrzędne punktu \(C\) są dodatnie (tak wynika z treści zadania), zatem:
$$m\gt0 \quad\text{oraz}\quad -\frac{1}{2}m+5\gt0 \\
m\gt0 \quad\text{oraz}\quad -\frac{1}{2}m\gt-5 \\
m\gt0 \quad\text{oraz}\quad m\lt10$$
Przy okazji zwróć uwagę, że zmienił się znak drugiej nierówności na przeciwny. Stało się tak dlatego, ponieważ mając postać \(-\frac{1}{2}m\gt-5\) wykonywaliśmy obustronne mnożenie przez \(-2\), czyli przez liczbę ujemną, a mnożąc lub dzieląc nierówność przez liczbę ujemną zawsze trzeba zmienić znak na przeciwny.
Wyszło nam więc, że \(m\) musi być większe od \(0\) i mniejsze od \(10\), stąd też dziedziną funkcji \(P(m)\) będzie \(m\in(0;10)\).
Krok 4. Wyznaczenie współrzędnych wierzchołka paraboli.
Wykresem funkcji kwadratowej jest parabola. Tutaj parabola będzie mieć ramiona skierowane do dołu (bo współczynnik \(a=-\frac{1}{4}\)). Sytuacja będzie więc wyglądać następująco (zwróć uwagę, że na poziomej osi mamy \(m\), a na pionowej pole \(P\)):
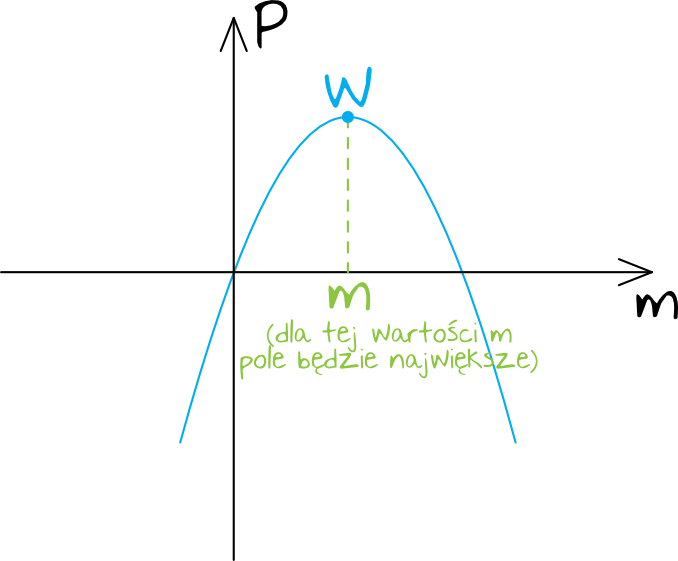
Chcemy się dowiedzieć, dla jakiego \(m\) osiągniemy jak największe pole \(P\). Z własności parabol wiemy, że parabola skierowana ramionami do dołu osiągnie swoją największą wartość w wierzchołku. Obliczmy zatem dla jakiej wartości \(m\) to największe pole jest przyjmowana, a pomoże nam w tym wzór na pierwszą współrzędną wierzchołka paraboli:
$$x_{W}=\frac{-b}{2a}$$
W naszym przypadku współczynnik \(a=-\frac{1}{4}\) oraz \(b=\frac{5}{2}\), zatem:
$$x_{W}=\frac{-\frac{5}{2}}{2\cdot(-\frac{1}{4})} \\
x_{W}=\frac{-\frac{5}{2}}{-\frac{1}{2}} \\
x_{W}=\left(-\frac{5}{2}\right):\left(-\frac{1}{2}\right) \\
x_{W}=\left(-\frac{5}{2}\right)\cdot(-2) \\
x_{W}=5$$
Tu warto przy okazji dodać, że otrzymany wynik mieści się w naszej dziedzinie, zatem wszystko jest w porządku.
Krok 5. Wyznaczenie współrzędnych punktu \(C\).
W poprzednim kroku otrzymaliśmy informację, że pole powierzchni będzie największe wtedy, gdy współrzędna \(x\) będzie równa \(5\). W naszym przypadku współrzędną \(x\) punktu \(C\) oznaczyliśmy jako \(m\), zatem to pole będzie największe wtedy, gdy \(m=5\). Współrzędna \(y\) punktu \(C\) jest opisana jako \(-\frac{1}{2}m+5\), zatem:
$$y_{C}=-\frac{1}{2}\cdot5+5 \\
y_{C}=-2\frac{1}{2}+5 \\
y_{C}=2\frac{1}{2}$$
To oznacza, że największe pole powierzchni otrzymamy wtedy, gdy \(C=(5;2\frac{1}{2})\).