Matura próbna z matematyki (poziom podstawowy) - Operon 2023
Łącznie do zdobycia jest 46 punktów, a sugerowany maksymalny czas rozwiązywania to 180 minut.
Matura 2024
Zadanie 1. (1pkt) Matura 2024Wartość wyrażenia \(-2(x-y)^2\) dla \(x=\frac{1}{\sqrt{3}}+3\) oraz dla \(y=\frac{\sqrt{3}}{3}-3\) jest równa:
Matura 2024
Zadanie 2. (1pkt) Matura 2024Połową liczby \(8^{22}\) jest:
Zadanie 3. (1pkt) Liczba \(log_{3}24-3log_{3}6\) jest równa:
Zadanie 4. (1pkt) Najmniejszą liczbą całkowitą, która nie należy do zbioru rozwiązań nierówności \(3-x\ge\frac{3}{5}x+7\) jest:
Zadanie 5. (1pkt) Na osi liczbowej zaznaczono przedział:

Zadanie 6. (1pkt) Dana jest funkcja \(f(x)=x^2+3x\).
Oceń prawdziwość poniższych zdań. Zaznacz P, jeśli zdanie jest prawdziwe, albo F - jeśli jest fałszywe.
Liczby \((-3)\) oraz \(0\) są miejscami zerowymi funkcji \(f(x)\)
Zbiorem wszystkich rozwiązań nierówności \(x^2+3x\ge0\) jest przedział \(\langle-3,0\rangle\)
Zadanie 7. (1pkt) Iloczynem wszystkich rozwiązań równania \(-3(x^2-5)(x+2)=0\) jest liczba:
Zadanie 8. (2pkt) Rozwiąż równanie \(2x^3-5x^2+8x-20=0\). Zapisz obliczenia.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie:
Aby rozwiązać to równanie, najprościej będzie skorzystać z metody grupowania. Całość obliczeń będzie wyglądać następująco:
$$2x^3-5x^2+8x-20=0 \\
x^2(2x-5)+4(2x-5)=0 \\
(x^2+4)\cdot(2x-5)=0$$
Aby powyższe równanie było równe \(0\), to wartość któregoś z tych nawiasów musi być równa \(0\), zatem:
$$x^2+4=0 \quad\lor\quad 2x-5=0 \\
x^2=-4 \quad\lor\quad 2x=5 \\
\text{brak rozw.} \quad\lor\quad x=\frac{5}{2}$$
Zadanie 9. (1pkt) Równanie \(\dfrac{5x(x+5)(3x-4)}{(4-3x)(5-x)^2}=0\) w zbiorze liczb rzeczywistych ma dokładnie:
Zadanie 10. (1pkt) W sklepie odzieżowym jest sezonowa obniżka cen. Przed obniżką za dwie bluzy i dwie pary spodni dresowych trzeba było zapłacić \(360 zł\). Po obniżce i po odliczeniu rabatu w wysokości \(30\%\) na bluzę oraz \(40\%\) na spodnie za jeden komplet, złożony z bluzy i spodni, trzeba zapłacić \(131 zł\).
Cenę bluzy \(x\) oraz cenę spodni dresowych \(y\) można obliczyć z układu równań:
Zadanie 11. (2pkt) Dana jest funkcja \(y=f(x)\), której zbiór wartości \(ZW_{f}=\langle-1,5)\). Funkcje \(g\) oraz \(h\) są określone za pomocą funkcji \(f\) następująco:
$$y=g(x)=f(x)+6 \\
y=h(x)=-f(x)$$
Dla każdej z funkcji \(y=g(x)\) oraz \(y=h(x)\) określono zbiór wartości.
Zadanie 11.1. Wybierz przedział spośród podanych w odpowiedziach A-F, który jest zbiorem wartości funkcji \(y=g(x)\).
Zadanie 11.2. Wybierz przedział spośród podanych w odpowiedziach A-F, który jest zbiorem wartości funkcji \(y=h(x)\).
Zadanie 12. (1pkt) Na rysunku jest przedstawiony fragment prostej przechodzącej przez punkty: \((-3, 2), (0, -3)\).
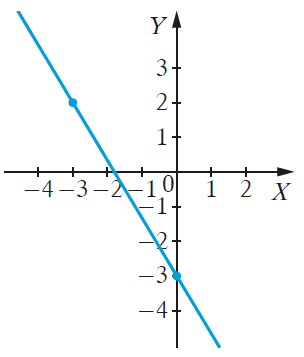
Prosta jest opisana równaniem:
Zadanie 13. (1pkt) Funkcja liniowa \(f(x)=3x-mx+15\) jest rosnąca dla:
Zadanie 14. (3pkt) Dana jest funkcja kwadratowa \(f(x)=-2(x+1)^2+5\).
Zadanie 14.1. Wierzchołek \(W\) paraboli ma współrzędne:
Zbiór wartości paraboli jest równy:
Zadanie 14.2. Oceń prawdziwość poniższych zdań. Zaznacz P, jeśli zdanie jest prawdziwe, albo F - jeśli jest fałszywe.
Funkcja \(f(x)\) jest malejąca w przedziale \((-\infty,-1)\).
Dla \(x=3\) funkcja przyjmuje wartości większe od \(5\).
Zadanie 14.3. Najmniejszą wartością funkcji \(f(x)\) w przedziale \(\langle-7,1\rangle\) jest:
Zadanie 15. (2pkt) Jednym z miejsc zerowych funkcji kwadratowej \(f(x)=x^2+bx+c\) jest liczba \((-2)\). Osią symetrii paraboli będącej wykresem funkcji jest prosta \(x=2\).
Oblicz wartości współczynników \(b\) i \(c\) we wzorze funkcji. Zapisz obliczenia.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie:
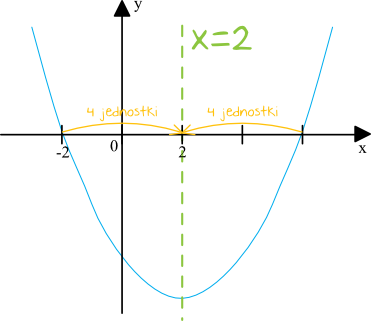
Krok 1. Wyznaczenie drugiego miejsca zerowego.
Z własności funkcji wynika, że oś symetrii przebiega dokładnie po środku między jednym i drugim miejscem zerowym funkcji kwadratowej. Skoro więc pierwszym miejscem zerowym jest \(x=-2\), to drugim miejscem zerowym musi być \(x=6\), co bardzo dobrze widać na poniższym rysunku:
Krok 2. Zapisanie wzoru funkcji w postaci iloczynowej.
Znając obydwa miejsca zerowe możemy zapisać wzór tej funkcji w postaci iloczynowej typu \(f(x)=a(x-x_{1})(x-x_{2})\). W takim razie:
$$f(x)=a(x-(-2))(x-6) \\
f(x)=a(x+2)(x-6)$$
Brakuje nam jeszcze współczynnika \(a\), ale możemy go odczytać z postaci ogólnej zapisanej w treści zadania, czyli zapisu \(f(x)=x^2+bx+c\). Przed \(x^2\) nie mamy żadnej liczby, czyli domyślnie stoi tam jedynka, czyli \(a=1\). To oznacza, że pełnym wzorem funkcji w postaci iloczynowej będzie \(f(x)=1\cdot(x+2)(x-6)\), czyli po prostu \(f(x)=(x+2)(x-6)\).
Krok 3. Zapisanie wzoru funkcji w postaci ogólnej.
Mając wzór w postaci iloczynowej, wystarczy przemnożyć przez siebie nawiasy i otrzymamy wtedy postać ogólną, zatem:
$$f(x)=(x+2)(x-6) \\
f(x)=x^2-6x+2x-12 \\
f(x)=x^2-4x-12$$
To oznacza, że poszukiwanymi współczynnikami są: \(b=-4\) oraz \(c=-12\).
Zadanie 16. (1pkt) Dany jest ciąg \((a_{n})\), w którym \(a_{n}=\sqrt[3]{5n-6}\) dla każdej liczby naturalnej \(n\ge2\). Dwunasty wyraz tego ciągu jest równy:
Zadanie 17. (2pkt) Dany jest ciąg \((a_{n})\), w którym \(a_{n}=\dfrac{7n-5}{5}\) dla każdej liczby naturalnej \(n\ge1\). Wykaż, że ciąg \((a_{n})\) jest arytmetyczny.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie:
$$a_{n+1}=\frac{7\cdot(n+1)-5}{5} \\
a_{n+1}=\frac{7\cdot(n+1)-5}{5} \\
a_{n+1}=\frac{7n+7-5}{5} \\
a_{n+1}=\frac{7n+2}{5}$$
$$a_{n+1}-a_{n}=\frac{7n+2}{5}-\frac{7n-5}{5} \\
a_{n+1}-a_{n}=\frac{7n+2-(7n-5)}{5} \\
a_{n+1}-a_{n}=\frac{7n+2-7n+5}{5} \\
a_{n+1}-a_{n}=\frac{7}{5}$$
Otrzymany wynik jest niczym innym jak po prostu różnicą ciągu arytmetycznego. Taki rezultat oznacza, że ciąg jest rzeczywiście arytmetyczny, co należało udowodnić.
Zadanie 18. (1pkt) Dany jest ciąg arytmetyczny \((a_{n})\), określony dla \(n\ge1\), w którym \(a_{1}=3\) oraz \(a_{3}=27\). W podanym ciągu \(a_{n}=99\) dla:
Zadanie 19. (1pkt) Dany jest ciąg geometryczny \((a_{n})\), określony dla \(n\ge1\), w którym \(a_{1}=-3\) oraz \(q=-2\). Suma ośmiu wyrazów tego ciągu jest równa:
Zadanie 20. (2pkt) W trójkącie prostokątnym \(ABC\) odcinek \(AB\) jest przeciwprostokątną oraz \(|AB|=11\), \(|AC|=9\) i \(|\sphericalangle ABC|=\beta\).
Zaznacz dwie odpowiedzi, tak aby dla każdej z nich wartości wyrażeń były prawidłowe.
Zadanie 21. (3pkt) Dany jest romb \(ABCD\), którego obwód wynosi \(40\sqrt{2}\), a kąt ostry ma miarę \(60°\).
Zadanie 21.1. Wyznacz długość dłuższej przekątnej rombu. Zapisz obliczenia.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Zadanie 21.2. Wyznacz pole rombu \(ABCD\). Zapisz obliczenia.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie:
Do obliczenia pola rombu skorzystamy z następującego wzoru, który wykorzystuje funkcję sinus:
$$P=a^2\cdot sin\alpha$$
Rozwiejmy jeszcze jedną wątpliwość - nie ma znaczenia, czy do obliczeń przyjmiemy \(sin60°\) czy \(sin120°\), bo obydwie te wartości są równe \(\frac{\sqrt{3}}{2}\). Podstawiając więc wszystkie znane dane do naszego wzoru, możemy zapisać, że:
$$P=(10\sqrt{2})\cdot sin60° \\
P=100\cdot2\cdot\frac{\sqrt{3}}{2} \\
P=200\cdot\frac{\sqrt{3}}{2} \\
P=100\sqrt{3}$$
Zadanie 22. (1pkt) Dany jest trójkąt \(ABC\), w którym \(|BC|=5\). Dwusieczna kąta \(ACB\) przecina bok \(AB\) w punkcie \(D\) takim, że \(|AD|=4\) oraz \(|BD|=3,2\). Bok \(AC\) trójkąta \(ABC\) ma długość:
Zadanie 23. (1pkt) Punkty \(A, B, C, D\) leżą na okręgu o środku \(O\). Kąt \(CAD\) ma miarę \(25°\) (zobacz rysunek).
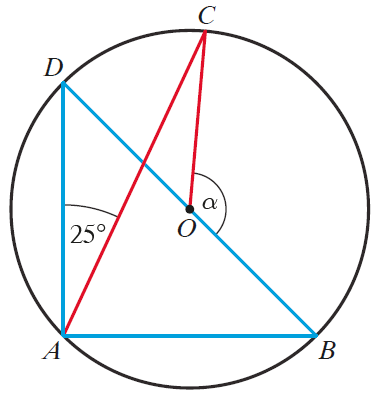
Miara zaznaczonego na rysunku kąta \(\alpha\) jest równa:
Zadanie 24. (1pkt) Dany jest czworokąt \(ABCD\) o bokach długości: \(3\sqrt{6}, 4\sqrt{6}, 5\sqrt{6}, 6\sqrt{6}\) oraz czworokąt \(KLMN\) do niego podobny, w którym najdłuższy bok ma długość \(24\sqrt{3}\). Obwód czworokąta \(KLMN\) jest równy:
Zadanie 25. (1pkt) Dana jest prosta \(k\) o równaniu \(y=-4x+3\).
Oceń prawdziwość poniższych zdań. Zaznacz P, jeśli zdanie jest prawdziwe, albo F - jeśli jest fałszywe.
Prosta o równaniu \(y=4x+5\) jest równoległa do prostej \(k\).
Prosta o równaniu \(y=\frac{1}{4}x+5\) jest prostopadła do prostej \(k\).
Zadanie 26. (1pkt) Na płaszczyźnie w kartezjańskim układzie współrzędnych \((x,y)\) dany jest okrąg \(O\) o środku w punkcie \(S=(2,-7)\) i promieniu \(6\).
Obrazem okręgu \(O\) w symetrii względem osi \(Oy\) jest okrąg opisany równaniem:
Zadanie 27. (4pkt) Na płaszczyźnie w kartezjańskim układzie współrzędnych \((x,y)\) dany jest trójkąt prostokątny \(ABC\). Wierzchołek \(A\) trójkąta leży na osi \(Ox\), a wierzchołek \(B\) leży na osi \(Oy\). Przeciwprostokątna \(AB\) tego trójkąta zawiera się w prostej o równaniu \(y=3x+12\). Do prostej zawierającej przyprostokątną \(BC\) należy punkt \(D=(6,6)\).
Wyznacz współrzędne wszystkich wierzchołków trójkąta \(ABC\). Zapisz obliczenia.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie:
Krok 1. Sporządzenie rysunku pomocniczego.
Rozwiązywanie zadania dobrze jest rozpocząć od prostego rysunku pomocniczego, zwłaszcza że opisywana sytuacja nie jest oczywista, bo wbrew pozorom to nie osie układu współrzędnych będą tworzyły nasz kąt prosty, a w dodatku punkt \(D\) będzie poza odcinkiem \(BC\). Całość będzie wyglądać mniej więcej w ten oto sposób:
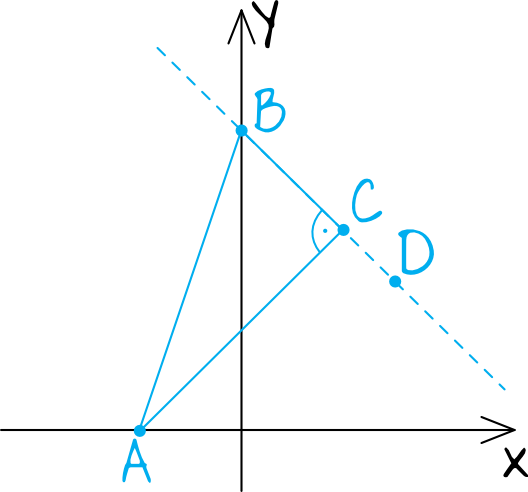
Krok 2. Wyznaczenie współrzędnych punktu \(B\).
Zacznijmy od najprostszej rzeczy, czyli wyznaczenia współrzędnych punktu \(B\). Skoro wierzchołek \(B\) leży na osi \(Oy\) to znaczy, że współrzędna \(x=0\). Współrzędna \(y\) będzie równa współczynnikowi \(b\) prostej o równaniu \(y=3x+12\), ale jeśli o tej własności nie pamiętamy, to zawsze do tego równania możemy podstawić \(x=0\), otrzymując:
$$y=3\cdot0+12 \\
y=0+12 \\
y=12$$
To oznacza, że \(B=(0,12)\).
Krok 3. Wyznaczenie współrzędnych punktu \(A\).
W bardzo podobny sposób wyznaczymy współrzędne wierzchołka \(A\). Wiemy, że leży on na osi \(Ox\), czyli że współrzędna \(y=0\). Aby wyznaczyć współrzędną \(x\) wystarczy podstawić \(y=0\) do równania \(y=3x+12\), zatem:
$$0=3x+12 \\
-3x=12 \\
x=-4$$
To oznacza, że \(A=(-4,0)\).
Krok 4. Wyznaczenie równania prostej \(BC\).
Wiemy, że do prostej \(BC\) należy punkt \(B=(0,12)\) oraz \(D=(6,6)\). Mamy więc klasyczną sytuację, w której musimy wyznaczyć równanie prostej przechodzącej przez dwa punkty. W tym celu możemy zastosować bardzo rozbudowany wzór z tablic lub też metodę układu równań. Prostsza jest metoda związana z układem, zatem do postaci \(y=ax+b\) podstawiamy najpierw współrzędne punktu \(B\), potem \(D\), otrzymując takie oto dwa równania tworzące układ:
\begin{cases}
12=0a+b \\
6=6a+b
\end{cases}
Ten układ możemy rozwiązać na różne sposoby, ale najprościej będzie chyba zauważyć, że z pierwszego równania wprost wynika, że \(b=12\). Tym samym podstawiając tę wartość do drugiego równania obliczymy współczynnik \(a\), zatem:
$$6=6a+12 \\
-6=6a \\
a=-1$$
Tym samym możemy stwierdzić, że prosta \(BC\) wyraża się równaniem \(y=-1x+12\), czyli po prostu \(y=-x+12\).
Krok 5. Wyznaczenie równania prostej \(AC\).
Prosta \(AC\) jest prostopadła do prostej \(BC\). Z własności prostych prostopadłych wiemy, że iloczyn ich współczynników kierunkowych \(a\) musi być równy \(-1\). Nasza prosta \(BC\) ma współczynnik \(a=-1\), więc prosta \(AC\) musi mieć współczynnik \(a=1\), ponieważ \((-1)\cdot1=-1\). Skoro tak, to prostą \(AC\) możemy zapisać jako \(y=1x+b\), czyli po prostu \(y=x+b\). Do pełnego wzoru tej prostej brakuje nam jeszcze współczynnika \(b\), a poznamy go podstawiając współrzędne punktu, który do tej prostej należy, czyli w tym przypadku współrzędne znanego punktu \(A=(-4,0)\). Otrzymamy wtedy:
$$0=-4+b \\
b=4$$
To oznacza, że prosta \(AC\) wyraża się równaniem \(y=x+4\).
Krok 6. Wyznaczenie współrzędnych punktu \(C\).
Punkt \(C\) jest miejscem przecięcia się prostej \(BC\) z prostą \(AC\). Z geometrycznej interpretacji układu równań wiemy, że aby poznać współrzędne takiego punktu wystarczy rozwiązać układ równań, który składa się z dwóch takich prostych, zatem:
\begin{cases}
y=-x+12 \\
y=x+4
\end{cases}
Korzystając z metody podstawiania, otrzymamy:
$$-x+12=x+4 \\
-2x=-8 \\
x=4$$
Podstawiając teraz wyznaczone \(x=4\) do dowolnego równania z układu (np. pierwszego) obliczymy współrzędną \(y\), zatem:
$$y=-4+12 \\
y=8$$
Tym samym możemy zapisać, że \(C=(4,8)\).
Zadanie 28. (1pkt) Suma długości wszystkich krawędzi sześcianu jest równa \(72 cm\). Objętość sześcianu jest równa:
Zadanie 29. (1pkt) Ze zbioru cyfr \({0, 1, 2, 3, 4, 5, 6, 7, 8, 9}\) losujemy czterokrotnie ze zwracaniem po jednej cyfrze i w kolejności losowania tworzymy z nich liczby czterocyfrowe.
Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A, B albo C oraz jej uzasadnienie 1., 2. albo 3.
Liczb czterocyfrowych o parzystych cyfrach jest:
Zadanie 30. (1pkt) Średnia arytmetyczna zestawu danych: \(3, 6, 9, 14\) jest o \(3\) mniejsza od średniej arytmetycznej zestawu danych: \(3, 6, 9, 14, x, x+4\).
Liczba \(x\) jest równa:
Zadanie 31. (4pkt) Właściciel działki postanowił ogrodzić płotem prostokątny plac, który ma służyć jako wybieg dla koni. Działka ma kształt trójkąta równoramiennego o podstawie \(360 m\) i wysokości opuszczonej na tę podstawę równej \(40 m\). Ogrodzony płotem plac będzie przylegać do podstawy działki (zobacz rysunek). W ogrodzeniu zostaną umieszczone \(2\) furtki każda z nich o szerokości \(2 m\) oraz brama wjazdowa o szerokości \(10 m\).
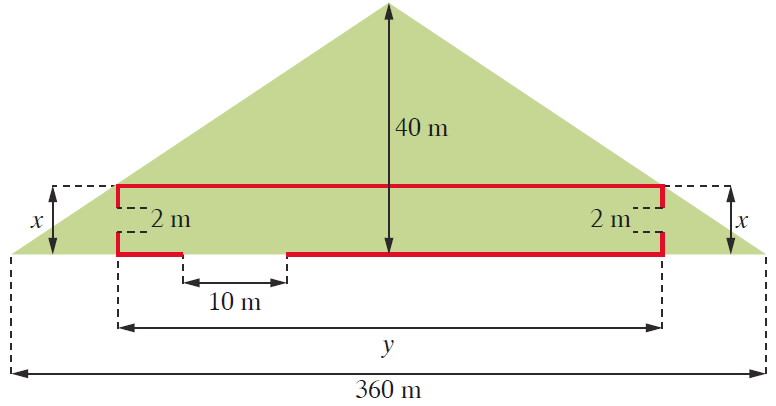
Oblicz wymiary \(x\) i \(y\) ogrodzonego placu, tak aby jego powierzchnia była największa, oraz łączną długość płotu ogradzającego plac. Zapisz obliczenia.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie:
Krok 1. Sporządzenie rysunku pomocniczego.
Wprowadźmy do zadania oznaczenia wierzchołków dwóch trójkątów (tak aby za chwilę się nie pogubić) i dopiszmy, że wysokość tego mniejszego trójkąta będzie równa \(40-x\):
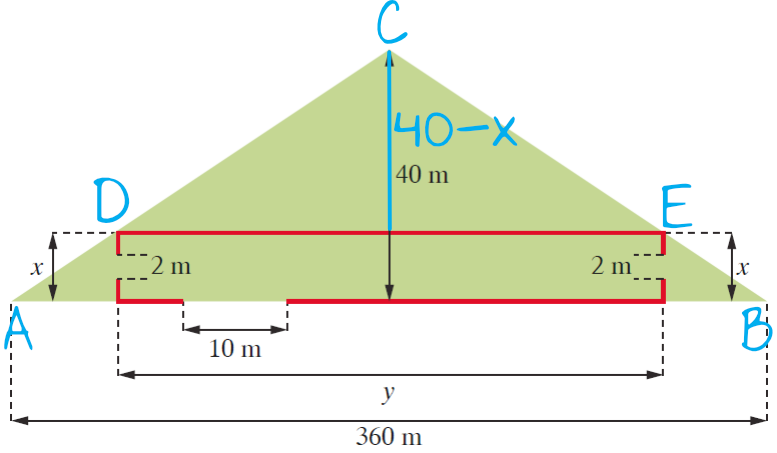
Krok 2. Obliczenie pola trójkąta \(ABC\).
Na początek obliczmy pole trójkąta \(ABC\). Mamy wszystkie potrzebne dane, ponieważ \(a=360\) oraz \(h=40\), zatem:
$$P_{ABC}=\frac{1}{2}\cdot360\cdot40 \\
P_{ABC}=7200$$
Krok 3. Zapisanie równań.
Kluczem do sukcesu będzie dostrzeżenie, że pole trójkąta \(ABC\) jest sumą pól trapezu \(ABED\) oraz trójkąta \(DEC\). Spróbujmy zapisać równania opisujące pola tych dwóch mniejszych figur, korzystając z oznaczeń które pojawiły się w pierwszym kroku.
Trapez \(ABED\) będzie mieć podstawy o długości \(a=360\) oraz \(b=y\), natomiast wysokość to \(h=x\). Jego pole zapisalibyśmy więc jako:
$$P_{ABED}=\frac{1}{2}\cdot(360+y)\cdot x \\
P_{ABED}=(180+\frac{1}{2}y)\cdot x \\
P_{ABED}=180x+\frac{1}{2}xy$$
Trójkąt \(DEC\) będzie mieć podstawę o długości \(a=y\) natomiast wysokość to \(h=40-x\). Jego pole zapisalibyśmy więc jako:
$$P_{DEC}=\frac{1}{2}\cdot y\cdot(40-x) \\
P_{DEC}=20y-\frac{1}{2}xy$$
Wiemy, że pole trójkąta \(ABC\) jest równe \(7200\) i tym samym jest to też suma pól powierzchni figury \(ABED\) oraz \(DEC\). Zapisalibyśmy zatem, że:
$$P_{ABC}=P_{ABED}+P_{DEC} \\
7200=180x+\frac{1}{2}xy+20y-\frac{1}{2}xy \\
7200=180x+20y \\
20y=-180x+7200 \quad\bigg/:20 \\
y=-9x+360$$
Dodatkowo możemy od razu zapisać, że pole prostokąta wyznaczymy ze wzoru:
$$P=x\cdot y$$
Krok 4. Zapisanie wzoru funkcji \(P(x)\).
Kluczem do sukcesu przy tego typu zadaniach jest poprawne zapisanie pola powierzchni w postaci funkcji z jedną zmienną, czyli zmienną \(x\). Podstawiając \(y=-9x+360\) do równania \(P=x\cdot y\), otrzymamy:
$$P=x\cdot(-9x+360) \\
P=-9x^2+360x$$
Otrzymaliśmy informację, że pole powierzchni prostokąta można opisać wzorem \(P=-9x^2+360x\). W ten sposób udało nam się zapisać wzór na pole z użyciem tylko jednej niewiadomej. Teraz całość możemy potraktować jak funkcję kwadratową (dla jakiejś wartości x otrzymamy konkretne pole \(P\)). Zapisalibyśmy więc, że \(P(x)=-9x^2+360x\).
Krok 5. Wyznaczenie współrzędnych wierzchołka paraboli.
Wykresem funkcji kwadratowej jest parabola. Tutaj parabola będzie mieć ramiona skierowane do dołu, ponieważ współczynnik \(a=-9\). Sytuacja będzie więc wyglądać następująco (zwróć uwagę, że na pionowej osi nie mamy \(y\), tylko pole \(P\)):
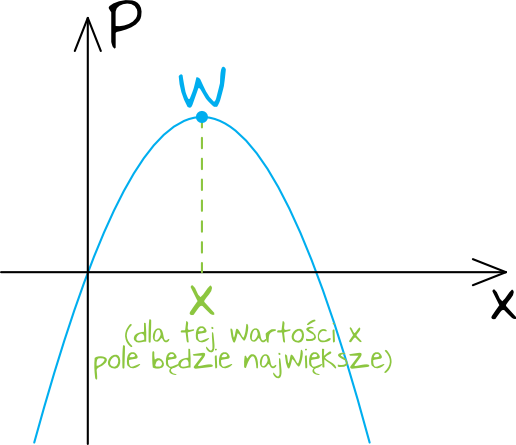
Chcemy się dowiedzieć, dla jakiego \(x\) to pole \(P\) będzie największe, a wiemy, że parabola skierowana ramionami do dołu osiągnie swoją największą wartość w wierzchołku. Obliczmy zatem dla jakiej długości \(x\) ta największa wartość jest przyjmowana, a pomoże nam w tym wzór na współrzędną \(x_{W}\) wierzchołka paraboli:
$$x_{W}=\frac{-b}{2a} \\
x_{W}=\frac{-360}{2\cdot(-9)} \\
x_{W}=\frac{-360}{-18} \\
x_{W}=20$$
Krok 6. Wyznaczenie długości drugiego boku prostokąta.
Wyliczyliśmy, że pole powierzchni będzie największe gdy jeden z boków prostokąta będzie miał długość \(x=20\). Zgodnie z treścią zadania, musimy jeszcze obliczyć długość drugiego boku, zatem korzystając z wcześniej zapisanego równania \(y=-9x+360\), otrzymamy:
$$y=-9\cdot20+360 \\
y=-180+360 \\
y=180$$
Krok 7. Obliczenie obwodu ogrodzenia.
Musimy jeszcze obliczyć obwód ogrodzenia. Jest to dość proste, ale musimy pamiętać, by od obwodu całego naszego prostokąta odjąć długości furtek i bram. Mamy jedną bramę o długości \(10m\) oraz dwie furtki po \(2m\) każda, zatem:
$$Obw=2\cdot180+2\cdot20-10-2\cdot2 \\
Obw=360+40-10-4 \\
Obw=386[m]$$