Przykładowy arkusz CKE
Arkusz maturalny zawiera 23 zadania zamkniętych oraz 10 zadań otwartych. Łącznie do zdobycia jest 50 punktów, a sugerowany maksymalny czas rozwiązywania to 170 minut.
W przypadku zadań zamkniętych musisz wybrać jedną z czterech odpowiedzi ABCD. Zadania otwarte rozwiąż na kartce papieru, a następnie przydziel sobie za nie odpowiednią liczbę punktów zgodnie z punktacją, która wyświetli się na ekranie. Zadania otwarte mają dodatkowo możliwość podejrzenia proponowanego rozwiązania, tak abyś mógł/a jak najrzetelniej przyznać sobie punkty za zadanie.
Jeżeli nie masz pewności jak rozwiązać dane zadanie, to możesz je opuścić i wrócić niego w dowolnej chwili. Kiedy uzupełnisz wszystkie zadania kliknij w przycisk zakończ. Na ekranie pojawi Ci się wtedy liczba zdobytych punktów oraz będziesz mieć możliwość przejrzenia swoich odpowiedzi wraz z pełnymi rozwiązaniami krok po kroku. Jeżeli jesteś gotowy/a to możesz przejść do pierwszego zadania.
Zadanie 1. (1pkt) Liczba \(15\) jest przybliżeniem z niedomiarem liczby \(x\). Błąd bezwzględny tego przybliżenia jest równy \(0,24\). Liczba \(x\) to:
Zadanie 2. (1pkt) Punkty \(E=(7,1)\) i \(F=(9,7)\) to środki boków, odpowiednio \(AB\) i \(BC\) kwadratu \(ABCD\). Przekątna tego kwadratu ma długość:
Zadanie 3. (1pkt) Liczba \(\left(\frac{3+\sqrt{3}}{\sqrt{3}}\right)^2\) jest równa:
Zadanie 4. (1pkt) Liczba \(3^{\frac{9}{4}}\) jest równa:
Zadanie 5. (1pkt) Funkcja wykładnicza określona wzorem \(f(x)=3^x\) przyjmuje wartość \(6\) dla argumentu:
Zadanie 6. (1pkt) Wyrażenie \(16-(3x+1)^2\) jest równe:
Zadanie 7. (1pkt) Wskaż równość prawdziwą:
Zadanie 8. (1pkt) Zbiorem rozwiązań nierówności \(\frac{2-x}{3}-\frac{2x-1}{2}\lt x\) jest przedział:
Zadanie 9. (1pkt) W klasie jest cztery razy więcej chłopców niż dziewcząt. Ile procent wszystkich uczniów tej klasy stanowią dziewczęta?
Zadanie 10. (1pkt) Reszta z dzielenia liczby \(55\) przez \(8\) jest równa:
Zadanie 11. (1pkt) Funkcja \(f\) przyporządkowuje każdej liczbie naturalnej większej od \(1\) jej największy dzielnik będący liczbą pierwszą. Spośród liczb: \(f(42\)), \(f(44)\), \(f(45)\), \(f(48)\) największa to:
Zadanie 12. (1pkt) Rysunek przedstawia ostrosłup prawidłowy czworokątny \(ABCDS\).

Kątem między krawędzią \(CS\), a płaszczyzną podstawy tego ostrosłupa, jest kąt:
Zadanie 13. (1pkt) Wykresem funkcji kwadratowej \(f\) jest parabola o wierzchołku \(W=(5,7)\). Wówczas prawdziwa jest równość:
Zadanie 14. (1pkt) Jeżeli kąt \(α\) jest ostry i \(tgα=\frac{3}{4}\), to \(\frac{2-cosα}{2+cosα}\) równa się:
Zadanie 15. (1pkt) Równanie \((2x-1)\cdot(x-2)=(1-2x)\cdot(x+2)\) ma dwa rozwiązania. Są to liczby:
Zadanie 16. (1pkt) Dane jest równanie \(3x+4y-5=0\). Z którym z poniższych równań tworzy ono układ sprzeczny?
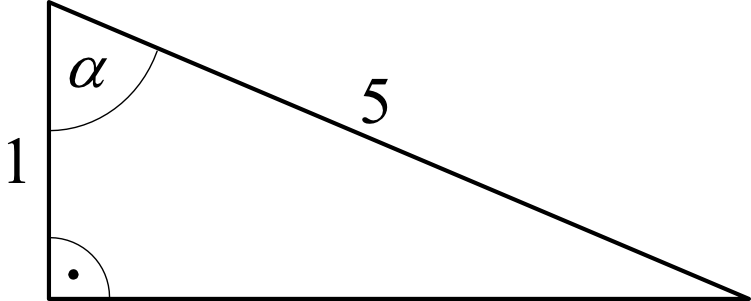
Zadanie 17. (1pkt) W trójkącie, przedstawionym na rysunku poniżej, sinus kąta ostrego \(α\) jest równy:
Zadanie 18. (1pkt) Tworząca stożka ma długość \(l\), a promień jego podstawy jest równy \(r\).
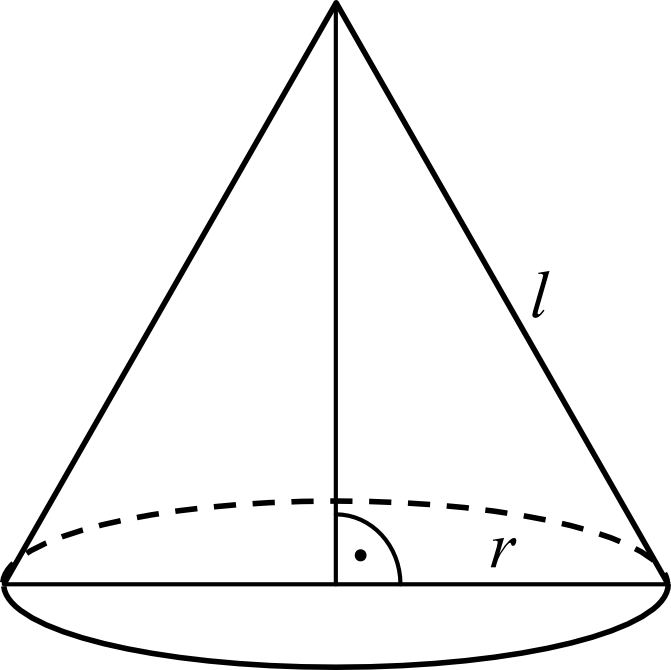
Powierzchnia boczna tego stożka jest \(2\) razy większa od pola jego podstawy. Wówczas:
Zadanie 19. (1pkt) Dane są dwa okręgi o promieniach \(10\) i \(15\). Mniejszy okrąg przechodzi przez środek większego okręgu. Odległość między środkami tych okręgów jest równa:
Zadanie 20. (1pkt) Każdy uczestnik spotkania dwunastoosobowej grupy przyjaciół uścisnął dłoń każdemu z pozostałych członków tej grupy. Liczba wszystkich uścisków dłoni była równa:
Zadanie 21. (1pkt) W dziewięciowyrazowym ciągu geometrycznym o wyrazach dodatnich pierwszy wyraz jest równy \(3\), a ostatni wyraz jest równy \(12\). Piąty wyraz tego ciągu jest równy:
Zadanie 22. (1pkt) Ciąg \((a_{n})\) jest określony wzorem \(a_{n}=(n+3)(n-5)\) dla \(n\ge 1\). Liczba ujemnych wyrazów tego ciągu jest równa:
Zadanie 23. (1pkt) Rzucamy jeden raz symetryczną sześcienną kostką do gry. Niech \(p_{i}\) oznacza prawdopodobieństwo wyrzucenia liczby oczek podzielnej przez \(i\). Wtedy:
Zadanie 24. (2pkt) Zbiorem rozwiązań nierówności \(ax+4\ge0\) z niewiadomą \(x\) jest przedział \((-\infty,2\rangle\). Wyznacz \(a\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy rozpiszesz nierówność w zależności od różnych współczynników \(a\), ale finalnie nie uda Ci się dojść do końcowego rozwiązania np. w wyniku błędu rachunkowego.
ALBO
• Gdy dostrzeżesz, że nierówności \(ax+4\ge0\) oraz \(x\le2\) są równoważne.
ALBO
• Gdy wyznaczysz miejsce zerowe funkcji: \(a=-\frac{4}{a}\).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Rozpatrzenie nierówności, gdy \(a=0\).
Chcąc rozwiązać nierówność \(ax+4\ge0\) nie możemy ot tak podzielić obu stron przez \(a\), bo nie wiemy czy przypadkiem \(a\) nie jest równe zero, a przecież w matematyce nie można wykonywać dzielenia przez zero.
Zatem gdy \(a=0\), to otrzymamy nierówność:
$$0\cdot x+4\ge0 \\
4\ge0$$
To oznacza, że gdy \(a=0\) to nierówność jest spełniona dla \(x\in R\), a więc to na pewno nie jest poprawna odpowiedź, gdyż my wiemy, że rozwiązaniem tej nierówności musi być przedział \((-\infty;2\rangle\).
Krok 2. Rozpatrzenie nierówności, gdy \(a\gt0\).
Wiemy już, że na pewno \(a\) nie jest równe zero, ale to w dalszym ciągu nie ułatwia nam zadania, bo nie wiemy czy \(a\) jest liczbą dodatnią, czy ujemną. Gdyby była to liczba ujemna, to przy dzieleniu musimy zmienić znak nierówności. Zobaczmy więc co nam wyjdzie z tej nierówności przy założeniu, że \(a\gt0\).
$$ax+4\ge0 \quad\bigg/-4 \\
ax\ge-4 \quad\bigg/:a \\
x\ge-\frac{4}{a}$$
To oznacza, że nasza nierówność dla \(a\gt0\) przyjmuje rozwiązania dla \(x\in\langle-\frac{4}{a};+\infty)\), co także nie pasuje nam do przedziału z treści zadania.
Krok 3. Rozpatrzenie nierówności, gdy \(a\lt0\).
Sprawdźmy zatem jak będzie wyglądać sytuacja, gdy \(a\) jest mniejsze od zera. To oznacza, że teraz dzieląc przez \(a\) musimy zmienić znak nierówności na przeciwny:
$$ax+4\ge0 \quad\bigg/-4 \\
ax\ge-4 \quad\bigg/:a \\
x\le-\frac{4}{a}$$
(Zwróć uwagę na zmianę znaku w ostatniej linijce. Dzielimy przez liczbę ujemną, więc zmienia się znak nierówności).
Otrzymaliśmy tym razem informację, że rozwiązaniem jest przedział \((-\infty;-\frac{4}{a}\rangle\) i taki przedział jest zbieżny z tym co mamy podane w treści zadania. Dzięki tej informacji możemy wyznaczyć \(a\), wystarczy przyrównać \(2\) do wyrażenia \(-\frac{4}{a}\). Zatem:
$$2=-\frac{4}{a} \\
2a=-4 \\
a=-2$$
Zadanie 25. (2pkt) Rozwiąż równanie \(\frac{x(x+1)}{x-1}=5x-4\), dla \(x\neq1\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy przekształcisz to równanie do postaci równania kwadratowego \(2x^2-5x+2=0\).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Rozwiązanie równania.
Rozwiązanie tego równania najlepiej jest rozpocząć od wymnożenia obydwu stron przez \((x-1)\). Możemy to zrobić, bo wiemy że \(x\neq1\), zatem:
$$\frac{x(x+1)}{x-1}=5x-4 \quad\bigg/\cdot(x-1) \\
x(x+1)=(5x-4)\cdot(x-1) \\
x^2+x=5x^2-5x-4x+4 \\
4x^2-10x+4=0 \quad\bigg/:2 \\
2x^2-5x+2=0$$
W ostatnim kroku zostało wykonane dzielenie przez \(2\), tak aby uprościć zapis i by wykonywać działania na mniejszych liczbach. Nie jest to działanie niezbędne do otrzymania prawidłowego wyniku.
Krok 2. Rozwiązanie powstałego równania kwadratowego.
Współczynniki: \(a=2,\;b=-5,\;c=2\)
$$Δ=b^2-4ac=(-5)^2-4\cdot2\cdot2=25-16=9 \\
\sqrt{Δ}=\sqrt{9}=3$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-5)-3}{2\cdot2}=\frac{5-3}{4}=\frac{2}{4}=\frac{1}{2} \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-5)+3}{2\cdot2}=\frac{5+3}{4}=\frac{8}{4}=2$$
Żadne z rozwiązań nie wyklucza się z założeniami, zatem to równanie ma dwa rozwiązania: \(x=\frac{1}{2}\) oraz \(x=2\).
Zadanie 26. (2pkt) Kwadrat \(K_{1}\) ma bok długości \(a\). Obok niego rysujemy kolejno kwadraty \(K_{2}, K_{3}, K_{4},...\) takie, że kolejny kwadrat ma bok połowę mniejszy od boku poprzedniego kwadratu (zobacz rysunek).
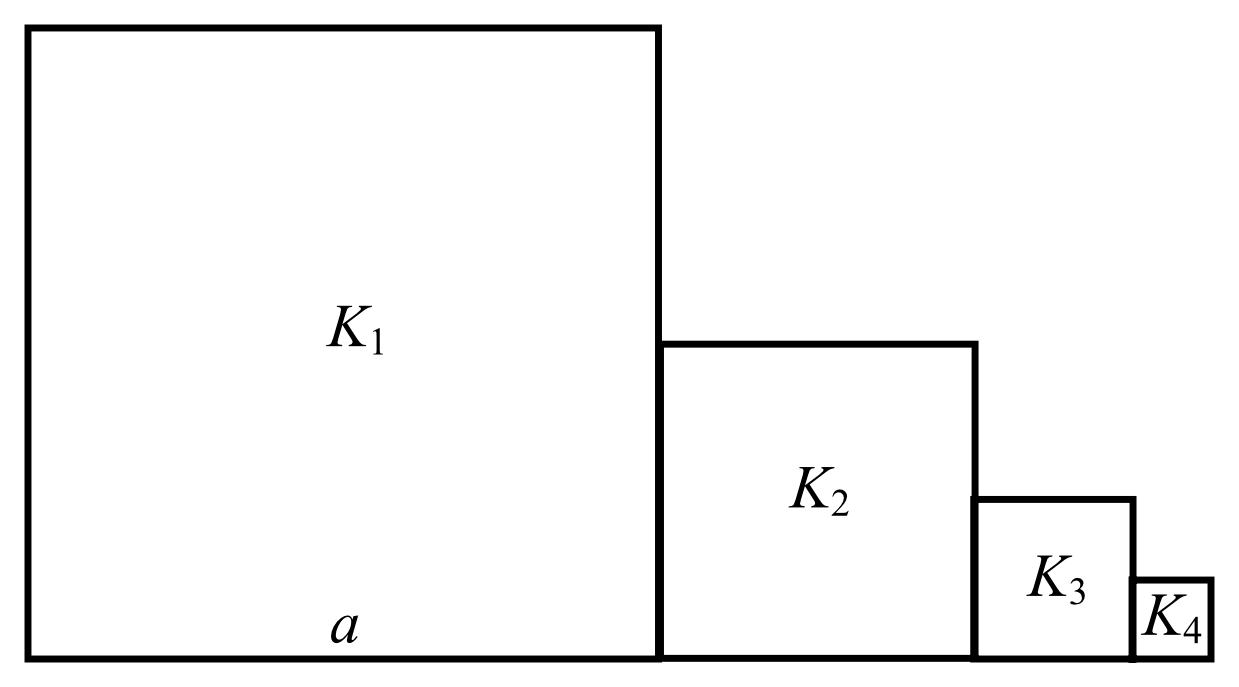
Wyznacz pole kwadratu \(K_{12}\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy zauważysz zależności pomiędzy długościami kolejnych boków (patrz: Krok 1.).
ALBO
• Gdy zauważysz, że pola kwadratów tworzą ciąg geometryczny, którego pierwszy wyraz jest równy \(a^2\), a iloraz jest równy \(q=\frac{1}{4}\).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Wyznaczenie długości boku kwadratu \(K_{12}\).
Pierwszy kwadrat ma długość boku równą \(a\).
Drugi kwadrat ma długość boku równą \(\frac{a}{2}\).
Trzeci kwadrat ma długość boku równą \(\frac{a}{2^2}\).
Czwarty kwadrat ma długość boku równą \(\frac{a}{2^3}\).
...
Dwunasty kwadrat ma długość boku równą \(\frac{a}{2^{11}}\).
Krok 2. Obliczenie pola kwadratu \(K_{12}\).
Podstawiając do wzoru na pole kwadratu długość boku równą \(\frac{a}{2^{11}}\) otrzymamy:
$$P=\left(\frac{a}{2^{11}}\right)^2=\frac{a^2}{2^{22}}$$
Zadanie 27. (2pkt) W pierścieniu kołowym cięciwa zewnętrznego okręgu ma długość \(10\) i jest styczna do wewnętrznego okręgu (zobacz rysunek).
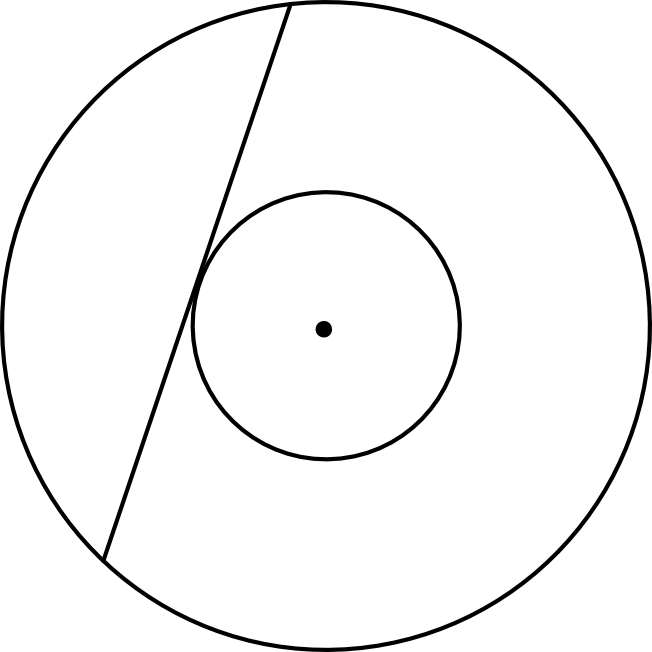
Wykaż, że pole tego pierścienia można wyrazić wzorem, w którym nie występują promienie wyznaczających go okręgów.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy zapiszesz wzór na pole pierścienia \(P=πR^2-πr^2\) (patrz: Krok 1.).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Zapisanie wzoru na pole pierścienia.
Pole pierścienia możemy zapisać jako różnicę między polem powierzchni dużego koła (o promieniu duże \(R\)) i małego (o promieniu małe \(r\)), zatem:
$$P=πR^2-πr^2=π(R^2-r^2)$$
No i teraz naszym zadaniem jest doprowadzenie do sytuacji w której pozbędziemy się wartości promieni.
Krok 2. Sporządzenie rysunku poglądowego.
Wiedząc, że styczna jest zawsze prostopadła do promienia okręgu, możemy stworzyć następujący trójkąt prostokątny:
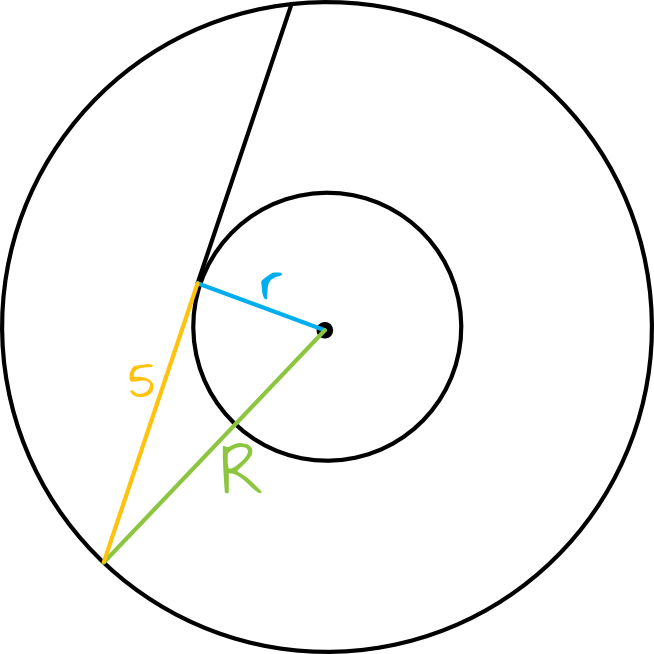
Krok 3. Wyznaczenie wartości wyrażenia \(R^2-r^2\) z Twierdzenia Pitagorasa.
Podstawiając do Twierdzenia Pitagorasa dane i oznaczenia z naszego rysunku otrzymamy:
$$r^2+5^2=R^2 \\
r^2+25=R^2 \\
25=R^2-r^2$$
Krok 4. Zakończenie dowodzenia.
Podstawiając wartość \(R^2-r^2\) do wzoru na pole pierścienia otrzymamy, że:
$$P=π(R^2-r^2) \\
P=25π$$
I taki zapis kończy nasze dowodzenie, bo udało nam się określić wzór na pole pierścienia bez występowania długości promieni.
Zadanie 28. (2pkt) Uzasadnij, że liczba \(4^{12}+4^{13}+4^{14}\) jest podzielna przez \(42\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy wyłączysz odpowiednie czynniki przed nawias, ale w taki sposób, że uda Ci się jedynie udowodnić, że ta liczba jest podzielna przez \(21\).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Aby udowodnić, że ta liczba jest podzielna przez \(42\) musimy zapisać to dodawanie w postaci mnożenia, wyłączając przed nawias odpowiednie czynniki. Jeśli uda nam się doprowadzić do sytuacji, w której jednym z czynników będzie liczba \(42\) lub jej wielokrotność, to dowód będziemy mogli uznać za zakończony.
Wyłączając przed nawias wartość \(4^{11}\) otrzymamy:
$$4^{12}+4^{13}+4^{14}=4^{11}\cdot(4+4^{2}+4^{3})= \\
=4^{11}\cdot(4+16+64)=4^{11}\cdot84=4^{11}\cdot2\cdot42$$
Doprowadzając liczbę do takiej postaci możemy uznać dowód za zakończony.
Zadanie 29. (2pkt) Na trójkącie o bokach długości \(\sqrt{7}\), \(\sqrt{8}\), \(\sqrt{15}\) opisano okrąg. Oblicz promień tego okręgu.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy udowodnisz, że jest to trójkąt prostokątny (patrz: Krok 1.).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Dostrzeżenie tego, że jest to trójkąt prostokątny.
Korzystając z Twierdzenia Pitagorasa możemy udowodnić, że ten trójkąt jest prostokątny:
$$a^2+b^2=c^2 \\
(\sqrt{7})^2+(\sqrt{8})^2=(\sqrt{15})^2 \\
7+8=15 \\
L=P$$
Krok 2. Skorzystanie z własności okręgów opisanych na trójkątach prostokątnych.

Jeśli okrąg jest opisany na trójkącie prostokątny, to długość średnicy tego okręgu jest równa długości przeciwprostokątnej trójkąta.
W związku z tym średnica tego okręgu ma długość \(\sqrt{15}\). Nas jednak interesuje długość promienia okręgu, a nie średnicy, zatem:
$$r=\frac{\sqrt{15}}{2}$$
Zadanie 30. (2pkt) Proste \(l\) i \(k\) przecinają się w punkcie \(A=(0,4)\). Prosta \(l\) wyznacza wraz z dodatnimi półosiami układu współrzędnych trójkąt o polu \(8\), zaś prosta \(k\) – trójkąt o polu \(10\). Oblicz pole trójkąta, którego wierzchołkami są: punkt \(A\) oraz punkty przecięcia prostych \(l\) i \(k\) z osią \(Ox\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz długości przyprostokątnych leżących na osi \(Ox\), czyli \(a=4\) oraz \(b=8\).
ALBO
• Gdy podasz współrzędne punktów przecięcia się z osią \(Ox\), czyli \(B=(4;0)\) oraz \(C=(5;0)\).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Sporządzenie rysunku poglądowego.
Spróbujmy naszkicować sobie powyższą sytuację, co jak się za chwilę okaże będzie kluczem do rozwiązania tego zadania.
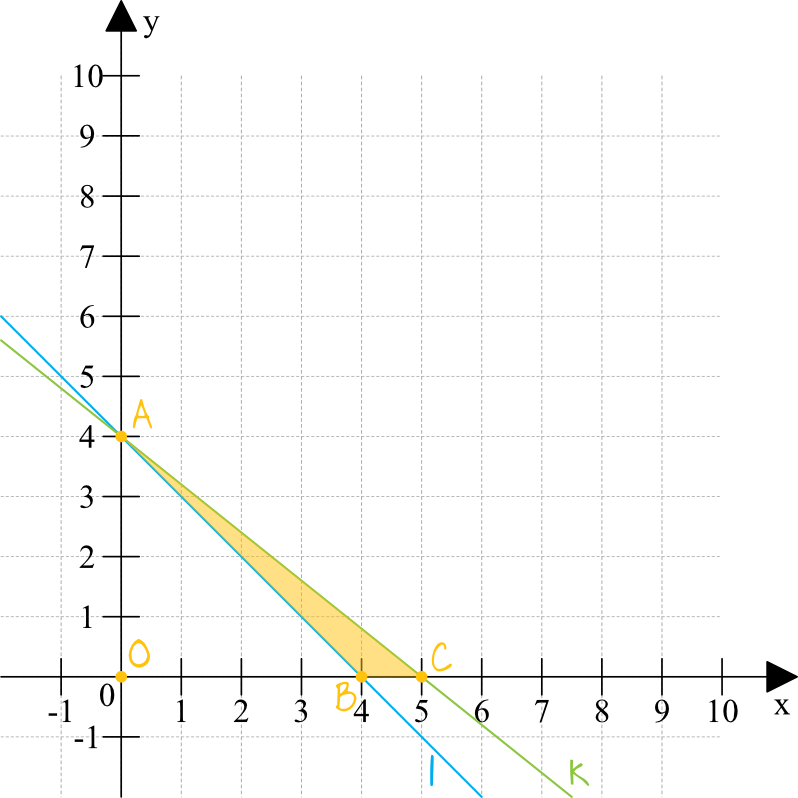
Dodatkowo oznaczyłem sobie początek układu współrzędnych jako punkt \(O\), tak aby móc dokładnie nazywać poszczególne trójkąty które będziemy sobie za chwilę rozpatrywać.
Krok 2. Obliczenie pola trójkąta \(ABC\).
Naszym zadaniem zgodnie z treścią zadania jest tak naprawdę obliczenie pola trójkąta \(ABC\). Jego pole powierzchni jest różnicą między polami trójkątów \(OCA\) oraz \(OBA\), zatem:
$$P_{ABC}=P_{OCA}-P_{OBA}$$
Z treści zadania wynika, że \(P_{OCA}=10\) oraz \(P_{OBA}=8\), zatem:
$$P_{ABC}=10-8 \\
P_{ABC}=2$$
Zadanie 31. (4pkt) Ala jeździ do szkoły rowerem, a Ola skuterem. Obie pokonują tę samą drogę. Ala wyjechała do szkoły o godzinie \(7{:}00\) i pokonała całą drogę w ciągu \(40\) minut. Ola wyjechała \(10\) minut później niż Ala, a pokonanie całej drogi zajęło jej tylko \(20\) minut. Oblicz, o której godzinie Ola wyprzedziła Alę.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy nie wykonasz jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy wprowadzisz sensowne oznaczenia i zapiszesz podstawowe relacje między nimi, dostrzegając że Ola jest dwa razy szybsza od Ali (patrz: Krok 1.).
ALBO
• Gdy wprowadzisz sensowne oznaczenia i zapiszesz wzory na prędkość jazdy obu dziewczynek np. \(v_{A}=\frac{s}{40}\) oraz \(v_{O}=\frac{s}{20}\).
2 pkt
• Gdy zapiszesz wzór na przebytą drogę do momentu spotkania się dziewczynek wykorzystując czas jazdy przynajmniej jednej z dziewczynek. Czyli przykładowo w zależności od oznaczeń możesz otrzymać równania typu: \(x=v_{O}\cdot(t-10)\) lub \(x=v_{A}\cdot(t+10)\), gdzie \(x\) to droga przebyta przez dziewczynki do momentu spotkania, a \(+/-10\) wynika z tego iż Ola wyjechała \(10\) minut później.
3 pkt
• Gdy zapiszesz prędkość lub drogę obydwu dziewczynek w formie równania, które pozwoli wyznaczyć poszukiwany czas np. \(v_{A}\cdot t=2v_{A}\cdot(t-10)\) (patrz: Krok 2) lub \(\frac{s}{40}t=\frac{s}{20}(t-10)\) lub \(\frac{s}{40}(t+10)=\frac{s}{20}t\).
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Wypisanie informacji z treści zadania.
Oznaczmy sobie następujące oznaczenia:
\(t\) - czas w minutach liczony od godziny \(7{:}00\)
\(s\) - odległość do pokonania
\(v_{O}\) - prędkość Oli
\(v_{A}\) - prędkość Ali
Z treści zadania wynika też, że Ola jest dwa razy szybsza od Ali (bo Ola jechała \(20\) minut, a Ala \(40\) minut). Zatem prawidłowa będzie też równość:
$$v_{O}=2v_{A}$$
Krok 2. Utworzenie i rozwiązanie równania.
Obie dziewczyny pokonały ten sam dystans. Skoro tak, to posłużmy się wzorem \(s=vt\) i zapiszmy w formie równania trasę każdej z dziewczyn:
$$v_{A}\cdot t=v_{O}\cdot(t-10)$$
(Odejmujemy u Oli \(10\) minut, bo wyruszyła \(10\) minut później, a zgodnie z naszymi oznaczeniami \(t\) symbolizuje czas liczony od \(7{:}00\))
Podstawiając do tego równania zależność \(v_{O}=2v_{A}\) otrzymamy:
$$v_{A}\cdot t=2v_{A}\cdot(t-10) \quad\bigg/:v_{A} \\
t=2\cdot(t-10) \\
t=2t-20 \\
-t=20 \\
t=20$$
Skoro \(t\) jest czasem liczonym w minutach od godziny \(7{:}00\), to znaczy że Ola wyprzedziła Alę o godzinie \(7{:}20\).
Zadanie 32. (5pkt) Dane są wierzchołki trójkąta \(ABC\): \(A=(2,2)\), \(B=(9,5)\) i \(C=(3,9)\). Z wierzchołka \(C\) poprowadzono wysokość tego trójkąta, która przecina bok \(AB\) w punkcie \(D\). Wyznacz równanie prostej przechodzącej przez punkt \(D\) i równoległej do boku \(BC\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy wyznaczysz współczynnik kierunkowy prostej \(AB\), czyli \(a=\frac{3}{7}\) (patrz: Krok 2) lub prostej \(BC\), czyli \(a=-\frac{2}{3}\) (patrz: Krok 5.).
2 pkt
• Gdy zapiszesz układ równań w skład którego wejdą równania prostej \(AB\) oraz \(CD\) (patrz: Krok 4.).
3 pkt
• Gdy wyznaczysz współrzędne \(D=(\frac{156}{29};\frac{100}{29})\).
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Sporządzenie rysunku poglądowego.
Spróbujmy zobrazować tą sytuację, zaznaczając poszczególne punkty w układzie współrzędnych.
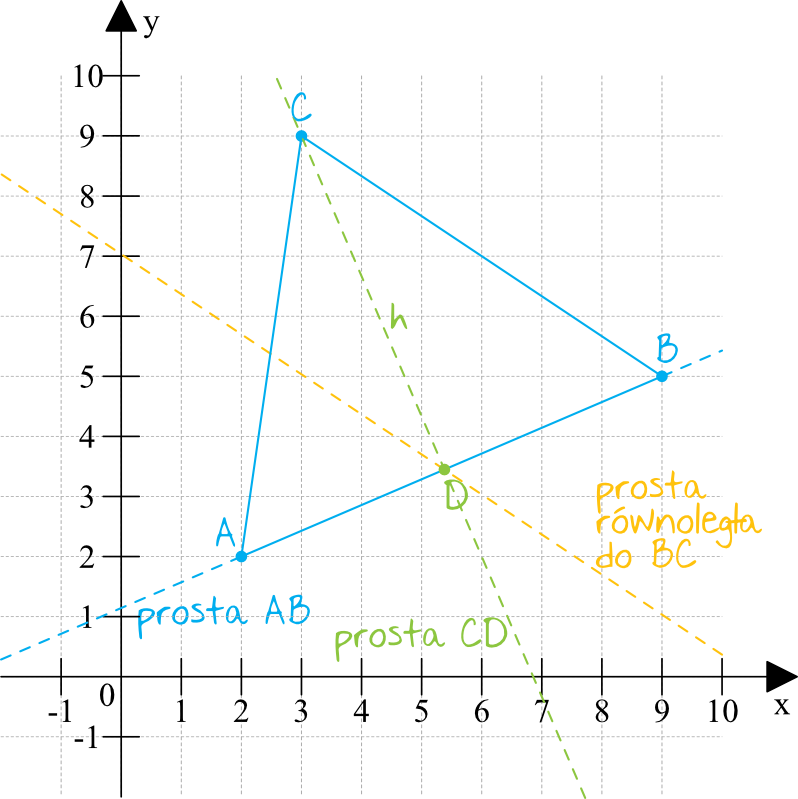
Ustalmy teraz co musimy obliczyć. Chcemy przede wszystkim wyznaczyć współrzędne punktu \(D\). Jednak żeby to zrobić, to musimy najpierw wyznaczyć równanie prostej przechodzącej przez punkty \(AB\), a następnie musimy znaleźć prostą prostopadłą do tej prostej, która przechodzi przez punkt \(C\). Punkt \(D\) będzie miejscem przecięcia się tych dwóch prostych. Na sam koniec musimy jeszcze wyznaczyć prostą równoległą do boku \(BC\), która przejdzie przez punkt \(D\). No to po kolei:
Krok 2. Wyznaczenie równania prostej \(AB\).
Możemy albo skorzystać ze wzoru na prostą przechodzącą przez punkty \(AB\), albo ułożyć i rozwiązać układ równań w którym do wzoru ogólnego \(y=ax+b\) podstawimy raz współrzędne punktu \(A\), a drugi raz współrzędne punktu \(B\).
\begin{cases}
2=2a+b \\
5=9a+b
\end{cases}
Odejmując to równanie stronami otrzymamy:
$$-3=-7a \\
a=\frac{3}{7}$$
Znając współczynnik \(a\) możemy z dowolnego równania wyznaczyć także współczynnik \(b\):
$$2=2\cdot\frac{3}{7}+b \\
2=\frac{6}{7}+b \\
b=\frac{8}{7}$$
To oznacza, że prosta \(AB\) jest opisana równaniem \(y=\frac{3}{7}x+\frac{8}{7}\).
Krok 3. Wyznaczenie równania prostej \(CD\).
Skoro prosta \(CD\) jest ma być prostopadła do prostej \(AB\), a to znaczy że iloczyn ich współczynników kierunkowych musi być równy \(-1\). Skoro prosta \(AB\) ma współczynnik \(a=\frac{3}{7}\), to prosta \(CD\) ma współczynnik \(a\) równy:
$$a\cdot\frac{3}{7}=-1 \\
a=-\frac{7}{3}$$
Wiemy już, że nasza prosta musi się wyrażać wzorem \(y=-\frac{7}{3}x+b\). Brakuje nam jeszcze współczynnika \(b\), ale skoro prosta przechodzi przez punkt \(C\) o znanych nam współrzędnych, to podstawiając te współrzędne do wzoru bez problemu obliczymy brakujący współczynnik:
$$y=-\frac{7}{3}x+b \\
9=-\frac{7}{3}\cdot3+b \\
9=-7+b \\
b=16$$
To oznacza, że prosta \(CD\) jest opisana równaniem \(y=-\frac{7}{3}x+16\).
Krok 4. Wyznaczenie współrzędnych punktu \(D\).
Zgodnie z geometryczną interpretacją układu równań, rozwiązanie układu równań dwóch prostych da wynik będący miejscem przecięcia się tych prostych, czyli w naszym przypadku otrzymamy współrzędne punktu \(D\).
\begin{cases}
y=\frac{3}{7}x+\frac{8}{7} \\
y=-\frac{7}{3}x+16
\end{cases}
Podstawiając wartość \(y\) z pierwszej funkcji do drugiej otrzymamy:
$$\frac{3}{7}x+\frac{8}{7}=-\frac{7}{3}x+16 \quad\bigg/\cdot21 \\
9x+24=-49x+336 \\
58x=312 \\
x=\frac{312}{58}=\frac{156}{29}$$
Podstawiajac wartość \(x=\frac{156}{29}\) do dowolnego z równań zapisanego wcześniej układu (do drugiego będzie chyba łatwiej, bo tam mamy tylko jeden ułamek) wyznaczymy współrzędną \(y\):
$$y=-\frac{7}{3}\cdot\frac{156}{29}+16 \\
y=-\frac{1092}{87}+16 \\
y=-\frac{364}{29}+16 \\
y=-\frac{364}{29}+\frac{464}{29} \\
y=\frac{100}{29}$$
Zatem \(D=\left(\frac{156}{29};\frac{100}{29}\right)\).
Krok 5. Wyznaczenie równania prostej \(BC\).
Zanim wyznaczymy prostą równoległą do prostej \(BC\), to musimy poznać równanie tej prostej \(BC\). Wyznaczymy je dokładnie w ten sam sposób co równanie prostej \(AB\) z kroku drugiego.
\begin{cases}
5=9a+b \\
9=3a+b
\end{cases}
Odejmujemy równanie stronami i otrzymujemy:
$$-4=6a \\
a=-\frac{4}{6}=-\frac{2}{3}$$
I w zasadzie tyle nam wystarczy, nie potrzebujemy już obliczać współczynnika \(b\). Wystarczy nam sam współczynnik \(a\) bo to właśnie on jest potrzebny do wyznaczenia prostej równoległej.
Krok 6. Wyznaczenie równania prostej równoległej przechodzącej przez punkt \(D\).
I to jest już ostatnia rzecz którą musimy zrobić - czyli wyznaczyć wzór prostej równoległej do \(BC\), która przechodzi przez punkt \(D\). Aby dwie proste były względem siebie równoległe to muszą mieć jednakowy współczynnik \(a\). My w poprzednim punkcie ten współczynnik sobie wyznaczyliśmy, zatem wiemy już, że ta poszukiwana prosta równoległa będzie opisana wzorem:
$$y=-\frac{2}{3}x+b$$
Brakuje nam współczynnika \(b\), ale bez problemu go wyznaczymy podstawiając do tej prostej współrzędne punktu \(D\), które wyliczyliśmy w czwartym kroku, zatem:
$$\frac{100}{29}=-\frac{2}{3}\cdot\frac{156}{29}+b \\
\frac{100}{29}=-\frac{312}{87}+b \\
\frac{100}{29}=-\frac{104}{29}+b \\
b=\frac{204}{29}$$
Szukana prosta równoległa ma więc równanie: \(y=-\frac{2}{3}x+\frac{204}{29}\).
Zadanie 33. (4pkt) Jacek bawi się sześciennymi klockami o krawędzi \(2cm\). Zbudował z nich jeden duży sześcian o krawędzi \(8cm\) i wykorzystał do tego wszystkie swoje klocki. Następnie zburzył budowlę i ułożył z tych klocków drugą bryłę – graniastosłup prawidłowy czworokątny. Wtedy okazało się, że został mu dokładnie jeden klocek, którego nie było gdzie dołożyć. Oblicz stosunek pola powierzchni całkowitej pierwszej ułożonej bryły do pola powierzchni całkowitej drugiej bryły i wynik podaj w postaci ułamka nieskracalnego.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz, że Jacek ma \(64\) klocki (patrz: Krok 1.).
2 pkt
• Gdy zapiszesz, że wymiary tego prostopadłościanu to \(6cm\times6cm\times14cm\) (patrz: Krok 3.).
3 pkt
• Gdy obliczysz pole powierzchni całkowitej bryły \(P_{G}=408cm^2\) (patrz: Krok 3.).
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Wyznaczenie liczby klocków, którymi bawi się Jacek.
Najpierw obliczmy objętość pojedynczego klocka, będzie to:
$$V=(2cm)^3=8cm^3$$
Teraz obliczmy objętość pierwszej bryły jaką ułożył Jacek, czyli sześciokąta o boku długości \(8cm\):
$$V=(8cm)^3=512cm^3$$
Skoro do ułożenia tego sześciokąta Jacek wykorzystał wszystkie swoje klocki, to znaczy że tych klocków ma:
$$512cm^3:8cm^3=64$$
Krok 2. Wyznaczenie wymiarów graniastosłupa prawidłowego czworokątnego.
Z treści zadania wynika, że Jacek do budowy graniastosłupa użył \(63\) klocków (bo jeden klocek został mu wolny).
Skoro Jacek ułożył graniastosłup prawidłowy czworokątny, to znaczy że ułożył bryłę która ma w podstawie kwadrat. Krótko mówiąc, podstawa (czyli tak jakby pierwsza warstwy bryły) musi wyglądać w taki sposób, że mamy np. \(2\) na \(2\) klocki, albo \(5\) na \(5\) klocków itd. W związku z tym do ułożenia samej podstawy Jacek musiał użyć np. \(1, 4, 9, 16, 25, 36\) lub \(49\) klocków. Innych możliwości nie ma, bo musi to być kwadrat liczby naturalnej.
W zasadzie możemy odrzucić wariant, w którym w podstawie jest jeden klocek (czyli byłaby to wieża wysoka na \(63\) klocki), bo gdyby tak wyglądała ta bryła, to przecież nie byłoby problemu dostawić także \(64\)-ty klocek na samą górę.
Musimy więc teraz sprawdzić, która z liczb \(4, 9, 16, 25, 36\) czy \(49\) jest dzielnikiem liczby \(63\). Taką liczbą jest jedynie \(9\), a więc wiemy już, że graniastosłup ma w podstawie \(3\times3\) klocki i jest wysoki na \(7\) klocków.
Krok 3. Obliczenie pola powierzchni całkowitej sześcianu i graniastosłupa.
Z treści zadania wiemy, że sześcian ma długość \(8cm\), zatem skoro każda ściana sześcianu ma powierzchnię \(P=8cm\cdot8cm\) i takich ścian mamy \(6\), to pole powierzchni całkowitej sześcianu jest równe:
$$P_{S}=6\cdot8^2 \\
P_{S}=6\cdot64 \\
P_{S}=384[cm^2]$$
Teraz musimy ustalić wymiary graniastosłupa. Skoro wymiary w klockach możemy wyrazić jako \(3\times3\times7\) klocków, a każdy klocek ma \(2cm\), to wymiary graniastosłupa w centymetrach będą następujące: \(6cm\times6cm\times14cm\). Czyli mamy dwie podstawy o powierzchni \(P_{p}=6cm\cdot6cm\) oraz cztery ściany boczne o powierzchni \(P_{b}=6cm\cdot14cm\). To oznacza, że pole powierzchni całkowitej graniastosłupa jest równe:
$$P_{G}=2P_{p}+4P_{b} \\
P_{G}=2\cdot6^2+4\cdot(6\cdot14) \\
P_{G}=2\cdot36+4\cdot84 \\
P_{G}=72+336 \\
P_{G}=408[cm^2]$$
Krok 4. Wyznaczenie stosunku pola powierzchni całkowitej pierwszej bryły względem drugiej.
Na sam koniec musimy jeszcze obliczyć stosunek tych pól powierzchni:
$$\frac{P_{S}}{P_{G}}=\frac{384cm^2}{408cm^2}=\frac{16}{17}$$