Egzamin gimnazjalny 2008 - matematyka
Egzamin zawiera 10 zadań zamkniętych oraz 4 zadania otwarte. Do zdobycia jest 25 punktów.
W przypadku zadań zamkniętych musisz wybrać jedną z czterech odpowiedzi ABCD. Zadania otwarte rozwiąż na kartce papieru, a następnie przydziel sobie za nie odpowiednią liczbę punktów zgodnie z punktacją, która wyświetli się na ekranie. Zadania otwarte mają dodatkowo możliwość podejrzenia proponowanego rozwiązania, tak abyś mógł/a jak najrzetelniej przyznać sobie punkty za zadanie.
Jeżeli nie masz pewności jak rozwiązać dane zadanie, to możesz je opuścić i wrócić niego w dowolnej chwili. Kiedy uzupełnisz wszystkie zadania kliknij w przycisk zakończ. Na ekranie pojawi Ci się wtedy liczba zdobytych punktów oraz będziesz mieć możliwość przejrzenia swoich odpowiedzi wraz z pełnymi rozwiązaniami krok po kroku. Jeżeli jesteś gotowy/a to możesz przejść do pierwszego zadania.
Zadanie 1. (1pkt) Poniższy diagram przedstawia procentowy udział źródeł energii zużywanej rocznie w USA.

Energia słoneczna to zaledwie \(1\%\) energii ze źródeł odnawialnych zużywanej rocznie w USA. Ile procent energii zużywanej rocznie w USA stanowi energia słoneczna?
Zadanie 2. (1pkt) Poniższy diagram przedstawia procentowy udział źródeł energii zużywanej rocznie w USA.

Na diagramie kołowym zaznaczono kąt \(AOB\). Ile stopni ma kąt \(AOB\)?
Zadanie 3. (1pkt) Gospodarstwa domowe w zależności od poziomu zamożności korzystają z różnych źródeł energii i zużywają różną jej ilość. Wykres ilustruje tę zależność dla Brazylii.
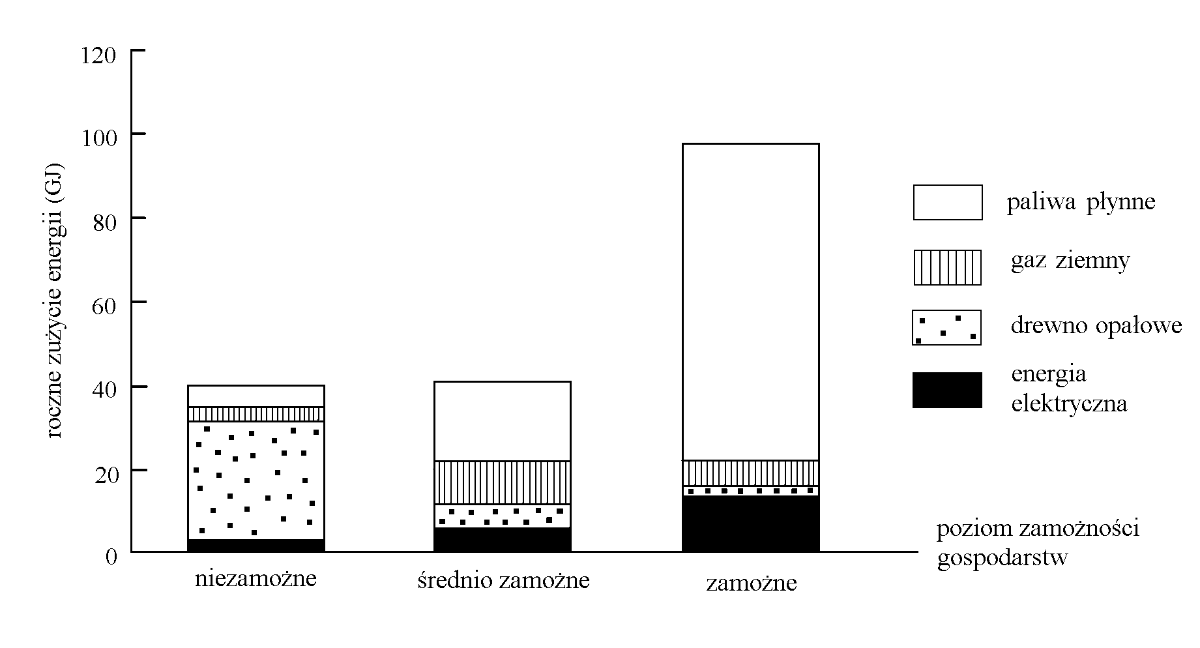
W którego typu gospodarstwach podstawowym źródłem zużywanej energii jest drewno opałowe?
Zadanie 4. (1pkt) Gospodarstwa domowe w zależności od poziomu zamożności korzystają z różnych źródeł energii i zużywają różną jej ilość. Wykres ilustruje tę zależność dla Brazylii.

Z analizy wykresu wynika, że w Brazylii:
Zadanie 5. (1pkt) W różnych publikacjach jako jednostka energii pojawia się czasem toe. \(1\) toe odpowiada energii, jaką uzyskuje się z \(1\) tony ropy naftowej i równa się \(41\;868 MJ\) (\(1MJ=1\;000\;000J\)). Ilu dżulom równa się \(1\) toe?
Zadanie 6. (1pkt) W którym z krajów wymienionych w tabeli roczne zużycie energii na mieszkańca jest największe?
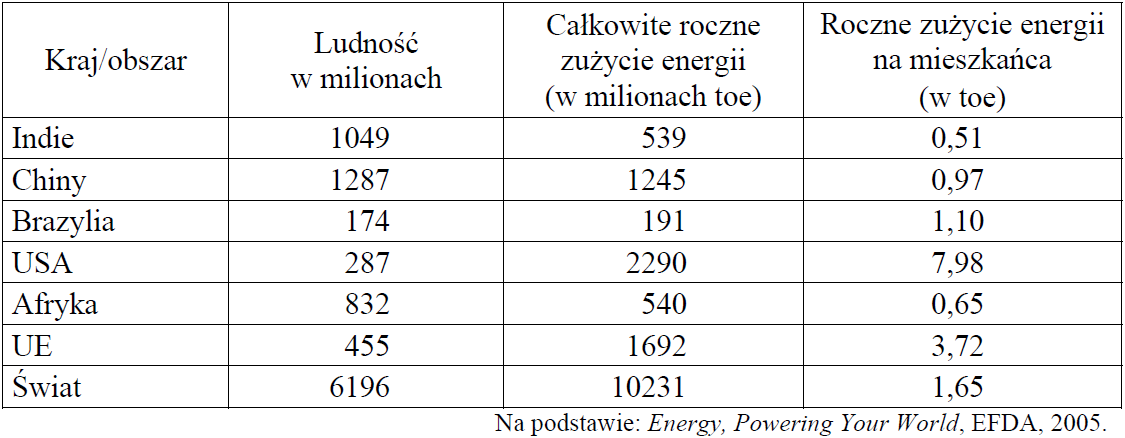
Zadanie 7. (1pkt) Które wyrażenie arytmetyczne pozwoli obliczyć, o ile milionów toe wzrosłoby całkowite roczne zużycie energii na świecie, gdyby w Indiach zużywano tyle samo energii na jednego mieszkańca, co w USA?

Zadanie 8. (1pkt) Z danych zapisanych w tabeli wynika, że rocznie:

Zadanie 9. (1pkt) Grupa złożona z trzynastu dziesięciolatków, jednego dwunastolatka i dwóch siedemnastolatków utworzyła Koło Ekologiczne. Średnia wieku członków tego koła jest równa:
Zadanie 10. (1pkt) W pewnym państwie liczba osób niepełnoletnich jest równa \(p\), pełnoletnich w wieku poniżej \(60\) lat jest o połowę mniej, a pozostałych dorosłych jest \(k\) razy mniej niż osób niepełnoletnich. Liczbie ludności tego państwa odpowiada wyrażenie:
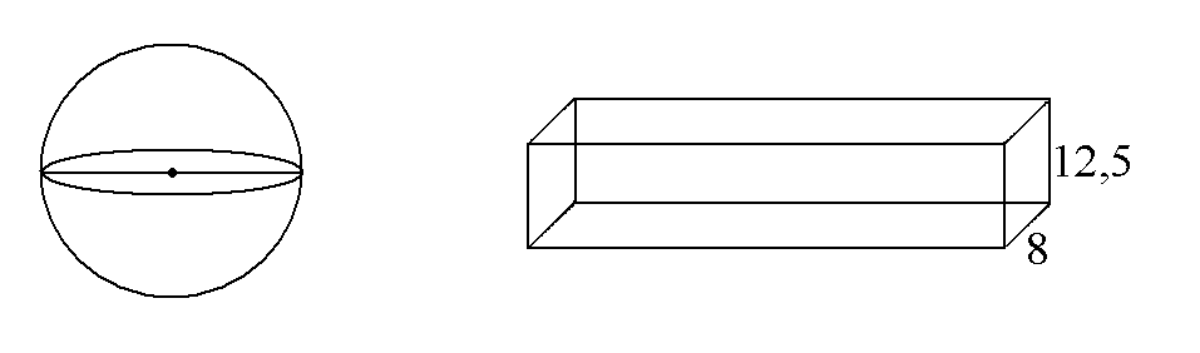
Zadanie 11. (6pkt) Kula o promieniu \(10cm\) i prostopadłościan, którego jedna ze ścian ma wymiary \(8cm\) i \(12,5cm\), mają taką samą objętość. Oblicz, ile razy pole powierzchni prostopadłościanu jest większe od pola powierzchni kuli. W obliczeniach przyjmij \(π=3\). Wynik zaokrąglij do części dziesiątych.
Użyteczne wzory dotyczące kuli:
\(V=\frac{4}{3}πr^3\)
\(P=4πr^2\)
\(r\) - promień kuli
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz jedynie objętość kuli (Krok 1.).
ALBO
• Gdy obliczysz jedynie pole powierzchni kuli (Krok 3.).
2 pkt
• Gdy obliczysz jedynie objętość i pole powierzchni kuli (Krok 1. i 3.).
ALBO
• Gdy obliczysz jedynie brakującą długość krawędzi prostopadłościanu (Krok 2.).
3 pkt
• Gdy obliczysz pole powierzchni prostopadłościanu (Krok 4.), ale nie obliczysz pola powierzchni kuli (Krok 3.).
4 pkt
• Gdy obliczysz pole powierzchni kuli i prostopadłościanu (Krok 3. i 4.), ale nie obliczysz stosunku powierzchni tych pól.
5 pkt
• Gdy obliczysz wszystkie elementy, ale otrzymany wynik jest niepoprawny z powodu błędu rachunkowego, bądź też nie wykonasz poprawnego zaokrąglenia.
6 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Obliczenie objętości kuli.
Korzystając z danych zawartych w treści zadania oraz przybliżenia \(π=3\) możemy bez przeszkód obliczyć objętość kuli:
$$V=\frac{4}{3}πr^3 \\
V=\frac{4}{3}π\cdot10^3 \\
V=\frac{4000}{3}π \\
V=\frac{4000}{3}\cdot3 \\
V=4000[cm^3]$$
Krok 2. Obliczenie brakującej długości krawędzi prostopadłościanu.
Do obliczenia pola powierzchni prostopadłościanu brakuje nam długości tej dłuższej krawędzi podstawy. Możemy ją obliczyć korzystając z informacji, że objętość kuli jest równa objętości prostopadłościanu, czyli \(V=4000cm^3\). W związku z tym:
$$V=abc \\
4000=a\cdot8\cdot12,5 \\
4000=100a \\
a=40[cm]$$
Krok 3. Obliczenie pola powierzchni kuli.
Istotą zadania jest policzenie pola powierzchni kuli i prostopadłościanu i porównanie tych dwóch wartości. Zacznijmy od pola powierzchni kuli:
$$P_{k}=4πr^2 \\
P_{k}=4π\cdot10^2 \\
P_{k}=400π \\
P_{k}=400\cdot3 \\
P_{k}=1200[cm^2]$$
Krok 4. Obliczenie pola powierzchni prostopadłościanu.
W kroku drugim obliczyliśmy brakującą długość krawędzi prostopadłościanu, więc teraz bez przeszkód możemy obliczyć jego pole powierzchni:
$$P_{p}=2ab+2ac+2bc \\
P_{p}=2\cdot40\cdot8+2\cdot40\cdot12,5+2\cdot8\cdot12,5 \\
P_{p}=640+1000+200 \\
P_{p}=1840[cm^2]$$
Krok 5. Porównanie pól powierzchni obydwu brył.
Musimy jeszcze odpowiedzieć na pytanie ile razy prostopadłościan ma większe pole powierzchni od kuli, zatem:
$$\frac{P_{p}}{P_{k}}=\frac{1840}{1200}\approx1,53\approx1,5$$
Zadanie 12. (2pkt) Postanowiono postawić przydomową elektrownię wiatrową. Zgodnie z zaleceniami maksymalna odległość końca obracającej się łopaty elektrowni od ściany domu powinna być równa podwojonej wysokości domu.
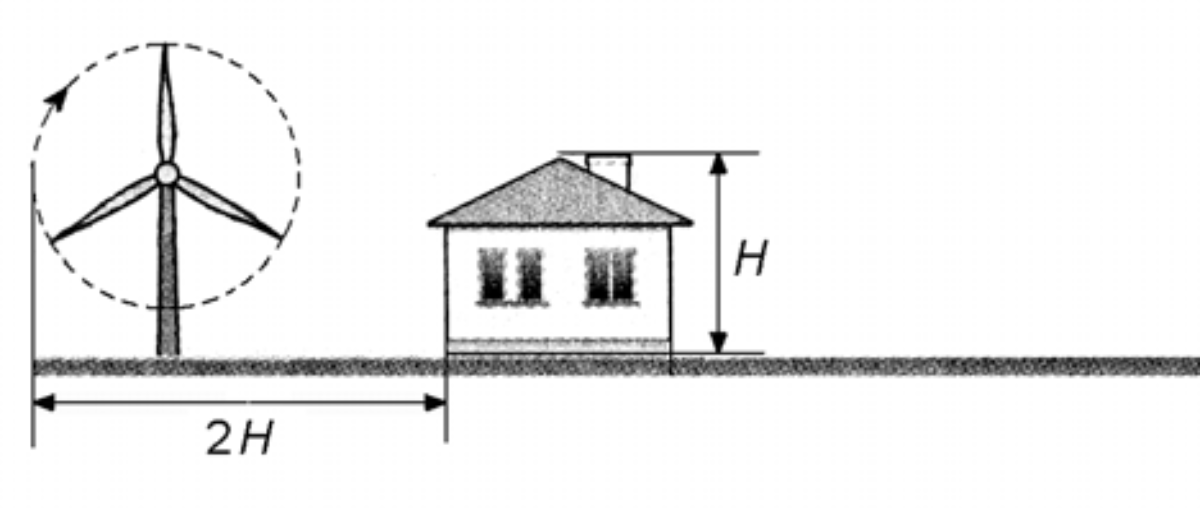
Wysokość słupa elektrowni wiatrowej jest równa \(16,5m\), a długość łopaty jest równa \(3,5m\). W jakiej odległości od ściany domu o wysokości \(H=12,3m\) powinien stać słup tej elektrowni wiatrowej? Która z danych podana została niepotrzebnie?
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz odległość słupa elektrowni od ściany domu (Krok 1.).
ALBO
• Gdy zapiszesz która dana jest niepotrzebna (Krok 2.).
2 pkt
• Gdy obliczysz odległość słupa elektrowni od ściany domu oraz zapiszesz która dana jest niepotrzebna (Krok 1. i 2.).
Wyjaśnienie:
Krok 1. Obliczenie odległości słupa elektrowni od ściany domu.
Zgodnie z danymi zapisanymi w treści zadania poszukiwaną odległość obliczymy w następujący sposób:
$$2\cdot12,3m-3,5m=24,6m-3,5m=21,1m$$
Krok 2. Wybranie niepotrzebnej danej.
Niepotrzebną daną w tym zadaniu była wysokość słupa elektrowni wiatrowej, która wynosi \(16,5m\).
Zadanie 13. (2pkt) Dla patrzącego z góry płytka chodnika ma kształt ośmiokąta, w którym kolejne boki są prostopadłe. Na rysunkach przedstawiono jego kształt, sposób układania płytek oraz niektóre wymiary w centymetrach.
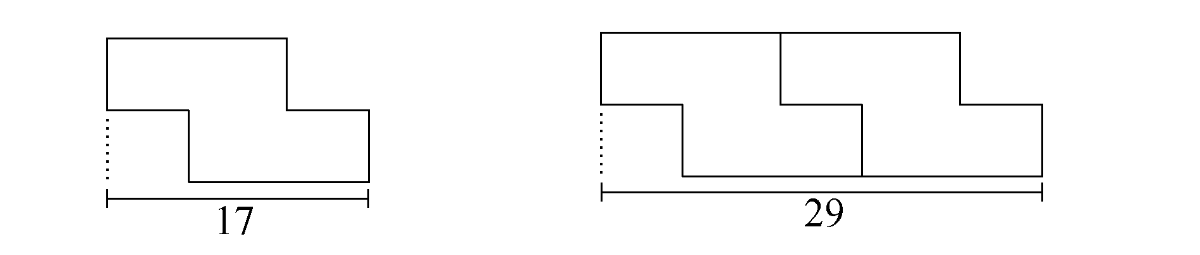
Ułożono sześć płytek.

Oblicz długość odcinka \(a\) oraz napisz wyrażenie algebraiczne, odpowiadające długości analogicznego odcinka dla pasa złożonego z \(n\) płytek.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz długość odcinka \(a\) (Krok 1.).
ALBO
• Gdy zapiszesz poprawnie poszukiwane wyrażenie algebraiczne (Krok 2.).
2 pkt
• Gdy obliczysz długość odcinka \(a\) oraz zapiszesz poprawnie poszukiwane wyrażenie algebraiczne (Krok 1. i 2.).
Wyjaśnienie:
Krok 1. Obliczenie długości odcinka \(a\).
Musimy zauważyć, że dołożenie każdej kolejnej płytki nie zwiększa nam długości chodnika o \(17cm\), bo płytki na siebie zachodzą. Dołożenie każdej kolejnej płytki zwiększa nam długość chodnika o \(29cm-17cm=12cm\).
Musimy obliczyć długość \(6\) płytek. Możemy więc to policzyć w taki sposób, że do pierwszej płytki o długości \(17cm\) dodano pięciu kolejnych płytek, z których każda zwiększa długość o \(12cm\). Otrzymamy zatem długość chodnika równą:
$$a=17cm+5\cdot12cm=17cm+60cm=77cm$$
Krok 2. Zapisanie wyrażenia algebraicznego.
Drugą częścią naszego zadania jest tak naprawdę ustalenie wzoru na długość chodnika. Skorzystamy już z tego co przeanalizowaliśmy sobie w pierwszym kroku, czyli z informacji że długość chodnika jest równa \(17cm\) pierwszej płytki plus \(12cm\) pomnożone przez tyle ile jest dodatkowo dołożonych płytek. Jeśli mamy mieć chodnik składający się z \(n\) płytek, to znaczy że do płytki początkowej trzeba dolożyć jeszcze \(n-1\) dodatkowych płytek, zatem nasz wzór miałby następującą postać:
$$17+12(n-1) \\
17+12n-12 \\
12n+5$$
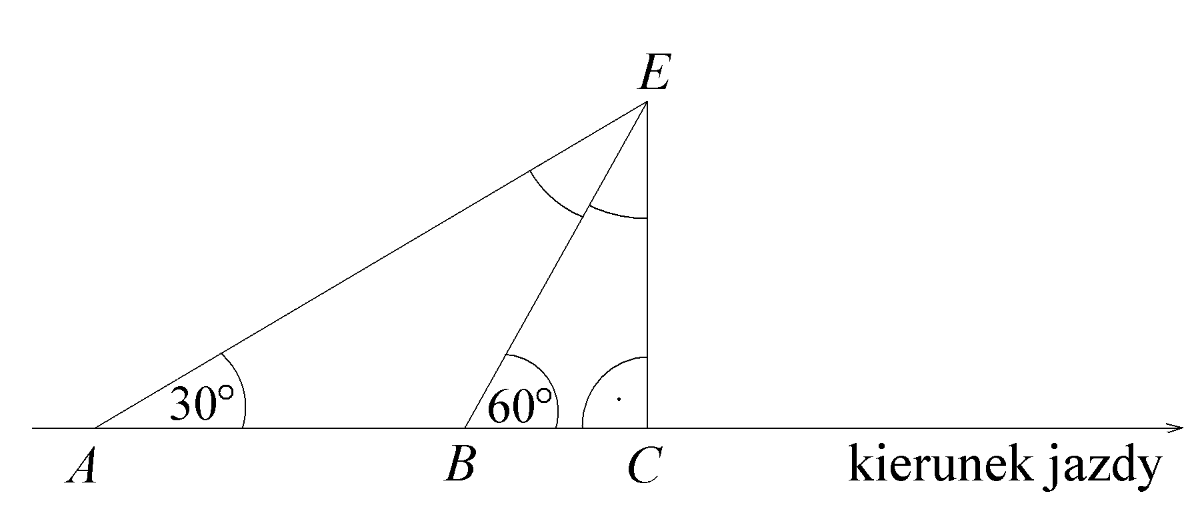
Zadanie 14. (5pkt) Jadąc długą, prostą drogą, Ewa widziała elektrownię wiatrową zaznaczoną na rysunku literą \(E\). Z punktu \(A\) widać było elektrownię pod kątem \(30°\) od kierunku jazdy, a z punktu \(B\) - pod kątem \(60°\). Długość odcinka \(AB\) jest równa \(20km\). Po pewnym czasie, przejeżdżając przez punkt \(C\), Ewa minęła elektrownię.
Wpisz na rysunku miary kątów zaznaczonych łukami (\(\sphericalangle BEC\) i \(\sphericalangle AEB\)). Oblicz odległość \((BE)\) elektrowni od punktu B oraz odległość \((CE)\) elektrowni od drogi. Wynik zaokrąglij do części dziesiątych, przyjmując że \(\sqrt{3}=1,73\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz miarę kąta \(BEC\)) (Krok 1.).
ALBO
• Gdy obliczysz miarę kąta \(AEB\)) (Krok 1.).
2 pkt
• Gdy obliczysz miary kątów \(BEC\) oraz \(AEB\) (Krok 1. i 2.).
3 pkt
• Gdy obliczysz długość odcinka \(BE\) (Krok 3.).
4 pkt
• Gdy obliczysz długość odcinka \(CE\) (Krok 4.), ale nie wykonasz poprawnego zaokrąglenia, bądź też otrzymany wynik jest błędny jedynie z powodu błędu rachunkowego.
5 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Obliczenie miary kąta \(BEC\).
Aby obliczyć miarę kąta \(BEC\) skorzystamy z własności trójkąta \(BCE\), którego suma kątów musi być równa \(180°\). W tym trójkącie znamy miary dwóch kątów, a nasz kąt \(BEC\) jest tym trzecim poszukiwanym, więc jego miarę obliczymy w następujący sposób:
$$|\sphericalangle BEC|=180°-60°-90°=30°$$
Krok 2. Obliczenie miary kąta \(AEB\).
Teraz musimy obliczyć miarę kąta \(AEB\). Możemy to zrobić w zasadzie na dwa sposoby:
I sposób - korzystając z trójkąta \(ABE\):
Spójrzmy na trójkąt \(ABE\). Znamy tu tylko miarę kąta \(EAB\), ale w prosty sposób możemy wyznaczyć miarę kąta \(ABE\), bowiem kąty \(ABE\) i \(EBC\) są przyległe. Zatem:
$$|\sphericalangle ABE|=180°-60°=120°$$
Znając miarę kąta \(ABE\) bez problemu obliczymy już miarę kąta \(AEB\), bowiem suma kątów w trójkącie \(ABE\) musi być równa jak zawsze \(180°\):
$$|\sphericalangle ABE|=180°-30°-120°=30°$$
II sposób - korzystając z trójkąta \(ACE\):
Kąt \(AEB\) to kąt \(AEC\) pomniejszony o miarę kąta \(BEC\). Kąt \(AEC\) ma miarę:
$$|\sphericalangle AEC|=180°-30°-90°=60°$$
Skoro kąt \(BEC\) ma miarę \(30°\), to nasz kąt \(AEB\) ma miarę:
$$|\sphericalangle AEB|=60°-30°=30°$$
Krok 3. Obliczenie długości boku \(BE\).
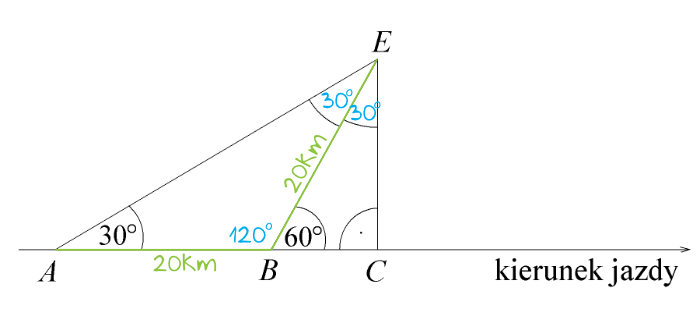
Na powyższym rysunku zaznaczone zostały te wszystkie kąty które już sobie przed chwilą wyznaczyliśmy. Kolejnym naszym zadaniem jest zgodnie z treścią wyznaczenie długości boku \(BE\). Aby tego dokonać musimy zauważyć, że trójkąt \(ABE\) jest trójkątem równoramiennym o ramionach \(AB\) oraz \(BE\) (zaznaczone na zielono). Wiemy to stąd, że ma on dwie identyczne miary kątów u swojej podstawy (po \(30°\)). A skoro tak, to oznacza, że długość boku \(BE\) jest dokładnie taka sama jak boku \(AB\). Długość boku \(AB\) jest podana i wynosi \(20km\), zatem także \(BE=20km\).
Krok 4. Obliczenie długości boku \(CE\).
Do wyznaczenia długości boku \(CE\) możemy wykorzystać własności trójkątów o kątach \(30°, 60°, 90°\). Znamy długość boku \(BE\), jest ona równa \(20km\). To z kolei oznacza, że długość boku \(BC\) jest dwa razy krótsza i wynosi \(10km\), a długość boku \(CE\) wynosi \(10\sqrt{3}km\approx17,3km\).
Jeżeli jednak nie znamy lub nie pamiętamy o własnościach trójkątów o kątach \(30°, 60°, 90°\) to możemy dostrzec, że trójkąt \(BCE\) jest połową pewnego trójkąta równobocznego, a odcinek \(CE\) jest tak naprawdę wysokością tego trójkąta:
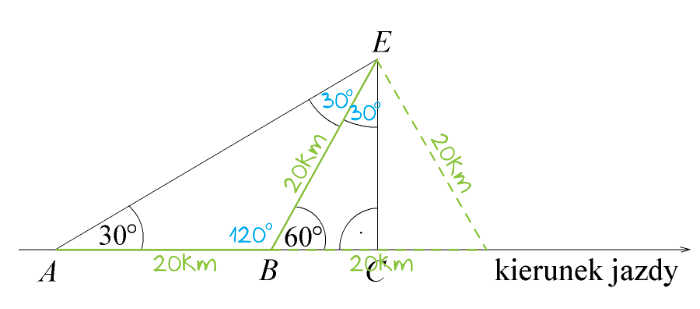
W tym momencie musimy dostrzec, że odcinek \(BC\) będzie w takim razie równy połowie długości odcinka \(BE\), czyli \(BC=10km\). Długość odcinka \(CE\) wyznaczymy więc już wprost z Twierdzenia Pitagorasa:
$$10^2+|CE|^2=20^2 \\
100+|CE|^2=400 \\
|CE|^2=300 \\
|CE|^2=100\cdot3 \\
|CE|=10\sqrt{3}\approx17,3km$$
Zgodnie z poleceniem otrzymany wynik został zaokrąglony do części dziesiętnych, zatem zadanie możemy uznać za rozwiązane.