Matura poprawkowa z matematyki (poziom podstawowy) - Sierpień 2023 (stara matura - formuła 2015)
Zadanie 1. (1pkt) Liczba \(log_{25}1-\frac{1}{2}log_{25}5\) jest równa:
Zadanie 2. (1pkt) Liczba \(3\sqrt{45}-\sqrt{20}\) jest równa:
Zadanie 3. (1pkt) W ramach wyprzedaży sezonowej płaszcz o początkowej wartości \(240 zł\) przeceniono na \(200 zł\). Zatem cenę tego płaszcza obniżono o:
Zadanie 4. (1pkt) Wartość wyrażenia \(\dfrac{3^{-1}}{\left(-\frac{1}{9}\right)^{-2}}\cdot81\) jest równa:
Zadanie 5. (1pkt) Wartość wyrażenia \((2-\sqrt{3})^2-(\sqrt{3}-2)^2\) jest równa:
Zadanie 6. (1pkt) W układzie współrzędnych \((x,y)\), punkt \((-8,6)\) jest punktem przecięcia prostych o równaniach:
Zadanie 7. (1pkt) Zbiorem wszystkich rozwiązań nierówności \(-3(x-1)\le\dfrac{5-3x}{3}\) jest przedział:
Zadanie 8. (1pkt) Równanie \((x^2-3x)(x^2+1)=0\) w zbiorze liczb rzeczywistych ma dokładnie:
Zadanie 9. (1pkt) Funkcja \(f\) jest określona dla każdej liczby rzeczywistej \(x\) wzorem \(f(x)=\dfrac{x-k}{x^2+1}\), gdzie \(k\) jest pewną liczbą rzeczywistą. Ta funkcja spełnia warunek \(f(1)=2\).
Wartość współczynnika \(k\) we wzorze tej funkcji jest równa:
Zadanie 10. (1pkt) Miejscem zerowym funkcji liniowej \(f\) jest liczba \(1\). Wykres tej funkcji przechodzi przez punkt \((-1,4)\). Wzór funkcji \(f\) ma postać:
Zadanie 11. (1pkt) Funkcja kwadratowa \(f\) jest określona wzorem \(f(x)=(x-13)^2-256\). Jednym z miejsc zerowych tej funkcji jest liczba \((-3)\). Drugim miejscem zerowym funkcji \(f\) jest liczba:
Zadanie 12. (1pkt) W układzie współrzędnych \((x,y)\) narysowano wykres funkcji \(y=f(x)\) (zobacz rysunek).
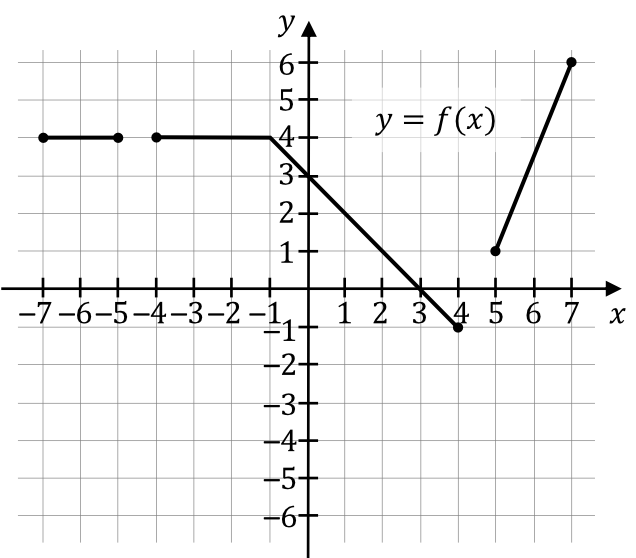
Funkcja \(f\) jest rosnąca w przedziale:
Zadanie 13. (1pkt) W układzie współrzędnych \((x,y)\) narysowano wykres funkcji \(y=f(x)\) (zobacz rysunek).
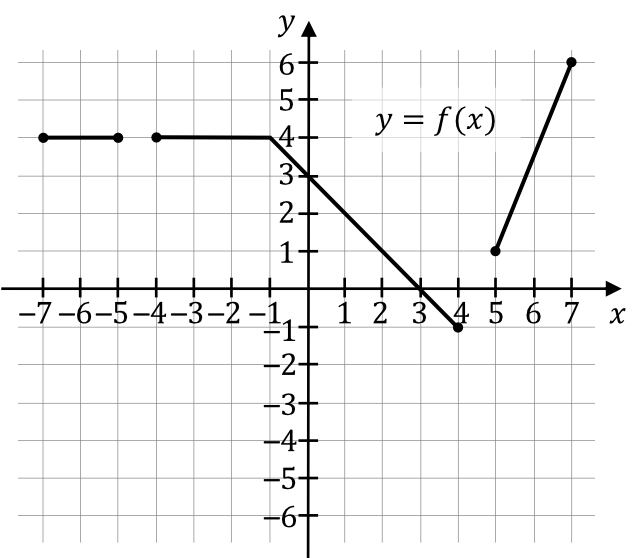
Funkcja \(g\) jest określona za pomocą funkcji \(f\) następująco: \(g(x)=f(-x)\) dla każdego \(x\in\langle-7,-5\rangle\cup\langle-4,4\rangle\cup\langle5,7\rangle\). Na jednym z rysunków A–D przedstawiono, w kartezjańskim układzie współrzędnych \((x,y)\), wykres funkcji \(y=g(x)\).
Wykres funkcji \(y=g(x)\) przedstawiono na rysunku:
Zadanie 14. (1pkt) Funkcja kwadratowa \(f\), określona wzorem \(f(x)=-(x-1)(x-5)\), przyjmuje wartość:
Zadanie 15. (1pkt) Ciąg \((a_{n})\) jest określony wzorem \(a_{n}=(-1)^n\cdot\frac{n+1}{2}\) dla każdej liczby naturalnej \(n\ge1\). Trzeci wyraz tego ciągu jest równy:
Zadanie 16. (1pkt) Czterowyrazowy ciąg \((-2, 1, x, y)\) jest geometryczny. Suma wszystkich wyrazów tego ciągu jest równa:
Zadanie 17. (1pkt) Koło ma promień równy \(3\). Obwód wycinka tego koła o kącie środkowym \(30°\) jest równy:
Zadanie 18. (1pkt) Kąt \(\alpha\) jest ostry i \(cos\alpha=\frac{2\sqrt{6}}{7}\). Sinus kąta \(\alpha\) jest równy:
Zadanie 19. (1pkt) W okręgu \(O\) kąt środkowy \(\beta\) oraz kąt wpisany \(\alpha\) są oparte na tym samym łuku. Kąt \(\beta\) ma miarę o \(40°\) większą od kąta \(\alpha\). Miara kąta \(\beta\) jest równa:
Zadanie 20. (1pkt) Pole trójkąta równobocznego o wysokości \(3\) jest równe:
Zadanie 21. (1pkt) Każdy z kątów wewnętrznych dziesięciokąta foremnego ma miarę:
Zadanie 22. (1pkt) Obwód trójkąta prostokątnego \(ABC\) jest równy \(L\). Na boku \(CB\) tego trójkąta obrano punkt \(E\), a na boku \(AB\) obrano punkt \(D\) tak, że \(DE||AC\) oraz \(|AD|:|DB|=3:4\) (zobacz rysunek).
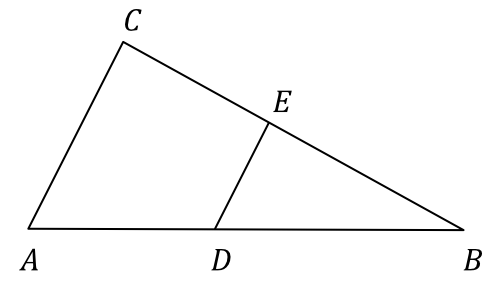
Obwód trójkąta \(BED\) jest równy:
Zadanie 23. (1pkt) W układzie współrzędnych \((x,y)\) dane są prosta \(k\) o równaniu \(y=\frac{3}{4}x-\frac{7}{4}\) oraz punkt \(P=(12,-1)\).
Prosta przechodząca przez punkt \(P\) i równoległa do prostej \(k\) ma równanie:
Zadanie 24. (1pkt) W układzie współrzędnych \((x,y)\) punkt \(A=(-1,-4)\) jest wierzchołkiem równoległoboku \(ABCD\). Punkt \(S=(2,2)\) jest środkiem symetrii tego równoległoboku.
Długość przekątnej \(AC\) równoległoboku \(ABCD\) jest równa:
Zadanie 25. (1pkt) Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą \(6\). Pole powierzchni całkowitej tego graniastosłupa jest równe:
Zadanie 26. (1pkt) Każda krawędź graniastosłupa prawidłowego sześciokątnego ma długość równą \(6\). Cosinus kąta nachylenia dłuższej przekątnej tego graniastosłupa do płaszczyzny podstawy graniastosłupa jest równy:
Zadanie 27. (1pkt) W ostrosłupie prawidłowym czworokątnym stosunek pola powierzchni bocznej do pola podstawy jest równy \(12\). Wynika stąd, że w tym ostrosłupie stosunek wysokości ściany bocznej do krawędzi podstawy jest równy:
Zadanie 28. (1pkt) Na diagramie przedstawiono rozkład wynagrodzenia brutto wszystkich stu pracowników pewnej firmy za styczeń 2023 roku.
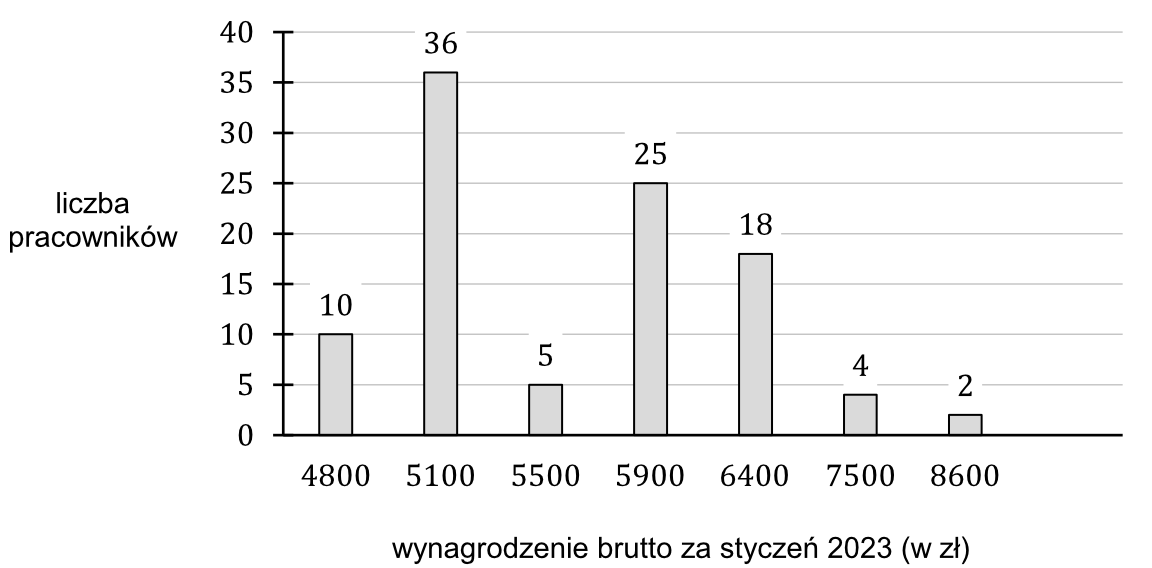
Średnia wynagrodzenia brutto wszystkich pracowników tej firmy za styczeń 2023 roku jest równa:
Zadanie 29. (1pkt) Wszystkich liczb naturalnych czterocyfrowych, w których zapisie dziesiętnym cyfry się nie powtarzają, jest:
Zadanie 30. (2pkt) Rozwiąż nierówność \(5-x^2\gt3x+1\)
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie:
Krok 1. Doprowadzenie nierówności do postaci ogólnej.
Zanim zaczniemy liczyć deltę, to musimy doprowadzić nierówność do postaci ogólnej, czyli musimy przenieść wszystkie wyrazy na lewą stronę:
$$5-x^2\gt3x+1 \\
-x^2-3x+4\gt0$$
Krok 2. Obliczenie miejsc zerowych wielomianu.
Współczynniki: \(a=-1,\;b=-3,\;c=4\)
$$Δ=b^2-4ac=(-3)^2-4\cdot(-1)\cdot4=9-(-16)=9+16=25 \\
\sqrt{Δ}=\sqrt{25}=5$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-3)-5}{2\cdot(-1)}=\frac{3-5}{-2}=\frac{-2}{-2}=1 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-3)+5}{2\cdot(-1)}=\frac{3+5}{-2}=\frac{8}{-2}=-4$$
Krok 3. Szkicowanie wykresu paraboli.
Współczynnik kierunkowy \(a\) jest ujemny, więc parabola będzie mieć ramiona skierowane do dołu. Zaznaczamy więc na osi wyznaczone miejsca zerowe \(x=-4\) oraz \(x=1\) (kropki będą niezamalowane, bo w nierówności wystąpił znak \(\gt\)) i rysujemy parabolę:
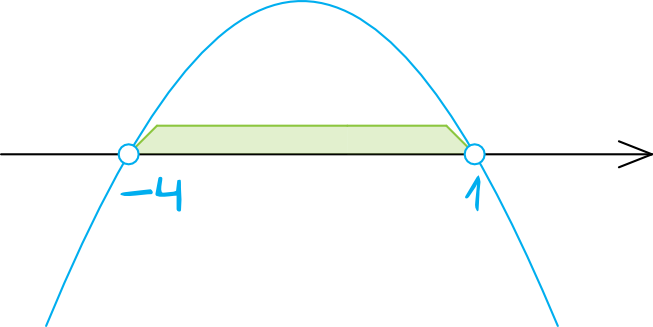
Krok 4. Odczytanie rozwiązania.
Interesują nas wyniki większe od zera, zatem interesuje nas to co znalazło się nad osią. To oznacza, że rozwiązaniem tej nierówności jest przedział:
$$x\in(-4;1)$$
Zadanie 31. (2pkt) Ciąg \((3x^2+5x, \quad x^2, \quad 20-x^2)\) jest arytmetyczny. Oblicz \(x\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie:
Dla trzech kolejnych wyrazów ciągu arytmetycznego zachodzi następująca własność:
$$a_{2}=\frac{a_{1}+a_{3}}{2}$$
Podstawiając do tego wzoru wyrazy z treści zadania, otrzymamy:
$$x^2=\frac{3x^2+5x+20-x^2}{2} \\
x^2=\frac{2x^2+5x+20}{2} \\
2x^2=2x^2+5x+20 \\
0=5x+20 \\
-20=5x \\
x=-4$$
Zadanie 32. (2pkt) Wykaż, że dla każdej liczby rzeczywistej dodatniej \(x\) i dla każdej liczby rzeczywistej dodatniej \(y\) takiej, że \(x\gt2y\), prawdziwa jest nierówność \(x^2+3xy-10y^2\gt0\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie:
Krok 1. Rozpisanie nierówności.
Kluczem do sukcesu w tym zadaniu będzie rozbicie \(-10y^2\) na sumę \(-4y^2\) oraz \(-6y^2\), a następnie odpowiednie pogrupowanie wyrazów. Obliczenia wyglądałyby następująco:
$$x^2+3xy-10y^2\gt0 \\
x^2+3xy-4y^2-6y^2\gt0 \\
x^2-4y^2+3xy-6y^2\gt0 \\
x^2-4y^2+3y(x-2y)\gt0$$
Wyrażenie \(x^2-4y^2\) możemy zgodnie ze wzorem skróconego mnożenia \(a^2-b^2=(a-b)(a+b)\) rozpisać jako \((x-2y)(x+2y)\). Wracając więc do naszego przykładu, otrzymamy postać:
$$(x-2y)(x+2y)+3y(x-2y)\gt0$$
Krok 2. Zakończenie dowodzenia.
Z treści zadania wiemy, że \(x\gt2y\), czyli że \(x-2y\gt0\). Spójrzmy teraz na naszą nierówność:
· w pierwszym nawiasie mamy \(x-2y\), co jak przed chwilą zapisaliśmy, musi być liczbą dodatnią;
· w drugim nawiasie mamy \(x+2y\) i to także jest wartość dodatnia, ponieważ z treści zadania wiemy, że \(x\) oraz \(y\) są dodatnie;
· następnie mamy \(+3y\), które także będzie dodatnie, bo \(y\) jest dodatni;
· i w ostatnim nawiasie ponownie mamy \(x-2y\), co jak już ustaliliśmy, będzie dodatnie.
Po lewej stronie mamy więc sytuację, w której mnożymy przez siebie dwie liczby dodatnie i dodajemy do tego iloczyn kolejnych dwóch dodatnich liczb. Otrzymany wynik będzie zatem na pewno większy od zera, co należało udowodnić.
Zadanie 33. (2pkt) Dany jest trapez równoramienny \(ABCD\), w którym podstawa \(CD\) ma długość \(6\), ramię \(AD\) ma długość \(4\), a kąty \(BAD\) oraz \(ABC\) mają miarę \(60°\) (zobacz rysunek).
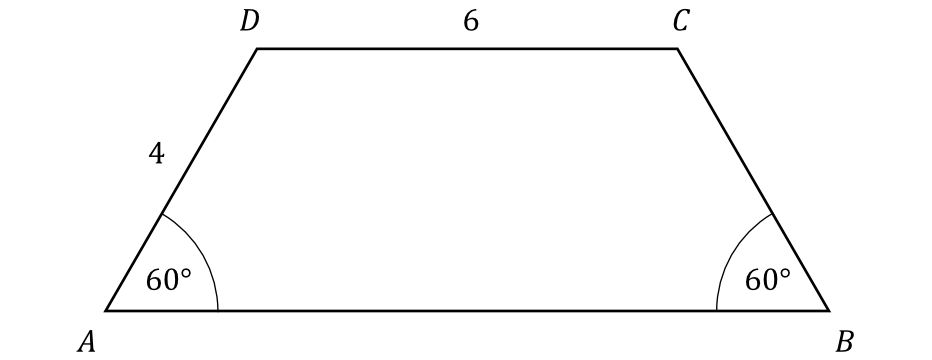
Oblicz pole tego trapezu.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie:
Krok 1. Sporządzenie rysunku pomocniczego.
Po dorysowaniu wysokości trapezu, sytuacja z treści zadania będzie wyglądać następująco:

Widzimy, że utworzył nam się tutaj kluczowy trójkąt o kątach \(30°, 60°, 90°\) i to właśnie z niego obliczymy potrzebne długości boków.
Krok 2. Obliczenie dolnej podstawy trapezu.
Spójrzmy na powstały trójkąt prostokątny. Zgodnie z własnościami trójkątów o kątach \(30°, 60°, 90°\), odcinek o długości \(x\) będzie miał miarę dwa razy mniejszą od przeciwprostokątnej (czyli w naszym przypadku od ramienia trapezu). To sprawia, że:
$$x=4:2 \\
x=2$$
Tym samym dolna podstawa trapezu będzie mieć długość:
$$a=2+6+2 \\
a=10$$
Krok 3. Obliczenie wysokości trapezu.
Ponownie spoglądamy na kluczowy trójkąt o kątach \(30°, 60°, 90°\). Zgodnie z własnościami takich trójkątów, wysokość całego trapezu będzie \(\sqrt{3}\) razy dłuższa od odcinka oznaczonego jako \(x\), który jak już ustaliliśmy, ma długość równą \(2\). To oznacza, że w takim razie \(h=2\sqrt{3}\).
Krok 4. Obliczenie pola trapezu.
Mając wszystkie potrzebne informacje możemy przejść do obliczenia pola trapezu, zatem:
$$P=\frac{1}{2}\cdot(a+b)\cdot h \\
P=\frac{1}{2}\cdot(10+6)\cdot2\sqrt{3} \\
P=\frac{1}{2}\cdot16\cdot2\sqrt{3} \\
P=16\sqrt{3}$$
Zadanie 34. (2pkt) Rozwiąż równanie \(\dfrac{2x-3}{3x-2}=\dfrac{1}{2x}\)
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie:
Krok 1. Zapisanie założeń.
Mamy klasyczne równanie wymierne, które w mianowniku ma niewiadomą \(x\). Z racji tego, iż na matematyce nie istnieje dzielenie przez \(0\), musimy zapisać założenia do naszego równania. Mianowniki naszych ułamków nie mogą być równe \(0\), stąd też zapisalibyśmy, że:
$$3x-2\neq0 \quad\land\quad 2x\neq0 \\
3x\neq2 \quad\land\quad x\neq0 \\
x\neq\frac{2}{3} \quad\land\quad x\neq0$$
Krok 2. Rozwiązanie równania.
Po zapisaniu założeń możemy przystąpić do rozwiązywania równania. Są różne podejścia do takich równań, ale najprościej będzie chyba wykonać tzw. mnożenie na krzyż, zatem:
$$(2x-3)\cdot2x=(3x-2)\cdot1 \\
4x^2-6x=3x-2 \\
4x^2-9x+2=0$$
Powstało nam równanie kwadratowe w postaci ogólnej, zatem z pomocą przyjdzie nam teraz delta:
Współczynniki: \(a=4,\;b=-9,\;c=2\)
$$Δ=b^2-4ac=(-9)^2-4\cdot4\cdot2=81-32=49 \\
\sqrt{Δ}=\sqrt{49}=7$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-9)-7}{2\cdot4}=\frac{9-7}{8}=\frac{2}{8}=\frac{1}{4} \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-9)+7}{2\cdot4}=\frac{9+7}{8}=\frac{16}{8}=2$$
Krok 3. Weryfikacja rozwiązań z założeniami.
Otrzymane rozwiązania musimy jeszcze zweryfikować z założeniami. W tym przypadku rozwiązania nie wykluczają się z założeniami, więc dopiero teraz możemy zapisać, że rozwiązaniami tego równania będą \(x=\frac{1}{4}\) oraz \(x=2\).
Zadanie 35. (2pkt) Ze zbioru pięciu liczb \({1,2,3,4,5}\) losujemy bez zwracania kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia \(A\) polegającego na tym, że obie wylosowane liczby są nieparzyste.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie:
Krok 1. Ustalenie liczby wszystkich możliwych zdarzeń elementarnych.
Losujemy ze zbioru pięciu liczb, a losowanie jest bez zwracania (czyli pierwsze losowanie jest spośród pięciu liczb, a drugie już tylko spośród czterech). To oznacza, że zgodnie z regułą mnożenia, wszystkich zdarzeń elementarnych będziemy mieć \(|Ω|=5\cdot4=20\).
Krok 2. Ustalenie liczby zdarzeń sprzyjających.
Chcemy, by obydwie wylosowane liczby były nieparzyste. Takich par nie jest dużo, możemy je nawet wypisać:
$$(1;3), (1;5) \\
(3;1), (3;5) \\
(5;1), (5;3)$$
To oznacza, że tylko sześć par spełnia warunki zadania, stąd też możemy zapisać, że \(|A|=6\).
Krok 3. Obliczenie prawdopodobieństwa.
Prawdopodobieństwo obliczymy korzystając ze wzoru:
$$P(A)=\frac{|A|}{|Ω|}=\frac{6}{20}=\frac{3}{10}$$
Zadanie 36. (5pkt) Punkty \(A=\left(\frac{22}{5},-\frac{21}{5}\right)\), \(B=(6,7)\) oraz \(C=(-9,2)\) są wierzchołkami trójkąta \(ABC\). Symetralna boku \(AB\) tego trójkąta przecina bok \(BC\) w punkcie \(D\). Oblicz współrzędne punktu \(D\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie:
Krok 1. Sporządzenie rysunku pomocniczego.
Rozwiązywanie zadania dobrze jest rozpocząć od narysowania przynajmniej szkicu całej sytuacji. Trójkąt \(ABC\) wraz z symetralną będzie wyglądał mniej więcej w ten oto sposób:
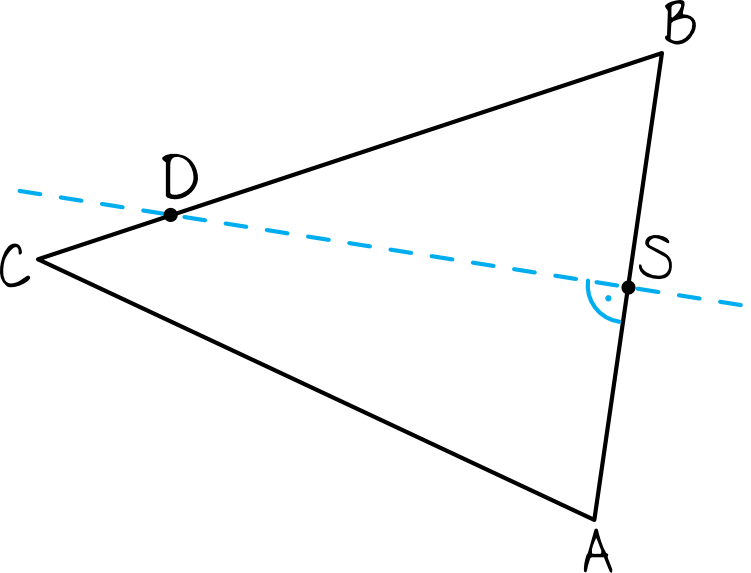
Krok 2. Wyznaczenie środka odcinka \(AB\).
Symetralna przechodzi zawsze przed środek odcinka, stąd też chcemy poznać jakie współrzędne ma środek odcinka \(AB\). W tym celu skorzystamy ze wzoru:
$$S=\left(\frac{x_{A}+x_{B}}{2};\frac{y_{A}+y_{B}}{2}\right)$$
I tu taka mała podpowiedź - aby ułatwić sobie obliczenia, można byłoby współrzędne punktu \(A\) zapisać w postaci ułamków dziesiętnych \(A=\left(4,4;\;-4,2\right)\). Pozwoli nam to wykonać szybkie i sprawne obliczenia na kalkulatorze:
$$S=\left(\frac{4,4+6}{2};\frac{-4,2+7}{2}\right) \\
S=\left(\frac{10,4}{2};\frac{2,8}{2}\right) \\
S=\left(5,2;\;1,4\right)$$
Krok 3. Wyznaczenie współczynnika kierunkowego prostej \(AB\).
Znając współrzędne punktów \(A\) oraz \(B\) możemy wyznaczyć wręcz pełne równanie prostej \(AB\). Nam jednak wystarczy poznanie współczynnika kierunkowego \(a\), bo to on przyda nam się później do zapisania równania symetralnej, która jest prostą prostopadłą. Możemy oczywiście wyznaczyć ten współczynnik budując odpowiedni układ równań, ale prościej i szybciej będzie skorzystać ze wzoru na współczynnik \(a\), zatem:
$$a=\frac{7-1,4}{6-5,2} \\
a=\frac{5,6}{0,8} \\
a=7$$
Krok 4. Wyznaczenie równania symetralnej odcinka \(AB\) (czyli prostej \(SD\)).
Symetralna odcinka \(AB\) jest prostą prostopadłą do tego boku. Aby dwie proste były względem siebie prostopadłe, to iloczyn ich współczynników kierunkowych musi być równy \(-1\). Skoro więc prosta \(AB\) ma ten współczynnik \(a=7\), to symetralna będzie miała współczynnik \(a=-\frac{1}{7}\), bo \(7\cdot\left(-\frac{1}{7}\right)=-1\). Skoro tak, to wiemy już, że prosta symetralna będzie wyrażać się równaniem \(y=-\frac{1}{7}+b\). Brakujący współczynnik \(b\) poznamy podstawiając współrzędne punktu \(S\) do tego równania, zatem:
$$1,4=-\frac{1}{7}\cdot5,2+b \\
\frac{7}{5}=-\frac{1}{7}\cdot\frac{26}{5}+b \\
\frac{7}{5}=-\frac{26}{35}+b \\
\frac{49}{35}=-\frac{26}{35}+b \\
b=\frac{75}{35}=2\frac{5}{35}=2\frac{1}{7}$$
To oznacza, że prosta symetralna wyraża się równaniem \(y=-\frac{1}{7}x+2\frac{1}{7}\).
Krok 5. Wyznaczenie równania prostej \(BC\).
Do wyznaczenia miejsca przecięcia się symetralnej z prostą \(BC\) potrzebujemy równania prostej \(BC\). Znamy współrzędne punktów \(B\) oraz \(C\), więc możemy albo skorzystać z długiego wzoru z tablic maturalnych, albo też z tradycyjnej metody układu równań. Skorzystajmy z tej drugiej metody, zatem podstawmy współrzędne punktów \(B\) oraz \(C\) do postaci \(y=ax+b\), otrzymując taki oto układ:
\begin{cases}
7=6a+b \\
2=-9a+b
\end{cases}
Odejmując te równania stronami, otrzymamy:
$$5=15a \\
a=\frac{1}{3}$$
Podstawiając teraz wyznaczone \(a=\frac{1}{3}\) do jednego z równań z układu (np. pierwszego), obliczymy brakujący współczynnik \(b\), zatem:
$$7=6\cdot\frac{1}{3}+b \\
7=2+b \\
b=5$$
To oznacza, że prosta \(BC\) wyraża się równaniem \(y=\frac{1}{3}x+5\).
Krok 6. Wyznaczenie współrzędnych punktu \(D\).
Z geometrycznej interpretacji układu równań wiemy, że współrzędne punktu \(D\) poznamy rozwiązując układ równań, który składa się z dwóch prostych przecinających się w tym punkcie - czyli w naszym przypadku będą to symetralna odcinka oraz prosta \(BC\). Musimy zatem rozwiązać następujący układ równań:
\begin{cases}
y=-\frac{1}{7}x+2\frac{1}{7} \\
y=\frac{1}{3}x+5
\end{cases}
Korzystając z metody podstawiania, otrzymamy:
$$-\frac{1}{7}x+2\frac{1}{7}=\frac{1}{3}x+5 \quad\bigg/\cdot21 \\
-3x+45=7x+105 \\
-10x=60 \\
x=-6$$
Podstawiając teraz współrzędną \(x=-6\) do wybranego równania z układu (np. drugiego), obliczymy brakującą współrzędną \(y\), zatem:
$$y=\frac{1}{3}\cdot(-6)+5 \\
y=-2+5 \\
y=3$$
Tym samym możemy stwierdzić, że \(D=(-6,3)\).