Matura z matematyki (poziom podstawowy) - Maj 2023
Łącznie do zdobycia jest 46 punktów, a sugerowany maksymalny czas rozwiązywania to 180 minut.
Zadanie 1. (1pkt) Na osi liczbowej zaznaczono sumę przedziałów.
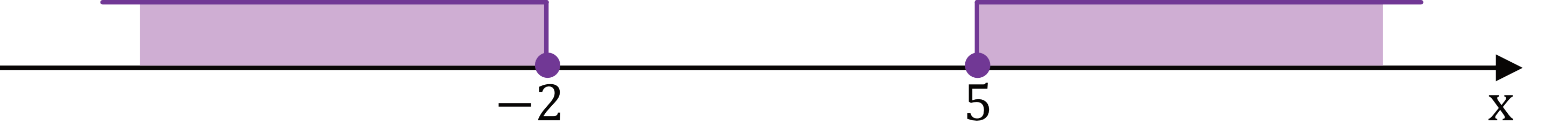
Zbiór zaznaczony na osi jest zbiorem wszystkich rozwiązań nierówności:
Zadanie 2. (1pkt) Liczba \(\sqrt[3]{-\frac{27}{16}}\cdot\sqrt[3]2\) jest równa:
Zadanie 3. (2pkt) Wykaż, że dla każdej liczby naturalnej \(n\ge1\) liczba \((2n+1)^2-1\) jest podzielna przez \(8\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy doprowadzisz liczbę do postaci \(4n(n+1)\), \(2n(2n+2)\), \(4(n^2+n)\) lub innej podobnej.
ALBO
• Gdy udowodnisz, że ta liczba jest podzielna przez \(4\).
2 pkt
• Gdy przeprowadzisz pełne dowodzenie.
Wyjaśnienie:
Korzystając ze wzorów skróconego mnożenia, liczbę z treści zadania możemy rozpisać w następujący sposób:
$$(2n+1)^2-1=4n^2+4n+1-1= \\
=4n^2+4n=4n(n+1)$$
Nasz zapis moglibyśmy dla lepszego zobrazowania przedstawić nawet jako \(4\cdot n\cdot(n+1)\). W tym zapisie \(n\) oraz \(n+1\) to kolejne liczby naturalne, a wiemy, że iloczyn dwóch kolejnych liczb naturalnych jest zawsze podzielny przez \(2\). Dodatkowo wyciągając czwórkę przed nawias udowodniliśmy, że liczba jest podzielna przez \(4\). Skoro zatem liczba da się rozłożyć na czynniki równe \(2\) oraz \(4\), to będzie też podzielna przez \(8\), co należało udowodnić.
Zadanie 4. (1pkt) Liczba \(log_{9}27+log_{9}3\) jest równa:
Zadanie 5. (1pkt) Dla każdej liczby rzeczywistej \(a\) wyrażenie \((2a-3)^2-(2a+3)^2\) jest równe:
Zadanie 6. (1pkt) Zbiorem wszystkich rozwiązań nierówności \(-2(x+3)\le\frac{2-x}{3}\) jest przedział:
Zadanie 7. (1pkt) Jednym z rozwiązań równania \(\sqrt{3}(x^2-2)(x+3)=0\) jest liczba:
Zadanie 8. (1pkt) Równanie \(\dfrac{(x+1)(x-1)^2}{(x-1)(x+1)^2}=0\) w zbiorze liczb rzeczywistych:
Zadanie 9. (3pkt) Rozwiąż równanie \(3x^3-2x^2-12x+8=0\).
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy doprowadzisz do postaci iloczynowej typu \((x^2-4)(3x-2)=0\)
ALBO
• Gdy otrzymasz przynajmniej jedno poprawne rozwiązanie.
2 pkt
• Gdy doprowadzisz równanie do postaci iloczynowej, w której nie będziemy mieć niewiadomej \(x\) podniesionej do kwadratu np. \((x-2)(x+2)(3x-2)=0\)
ALBO
• Gdy doprowadzisz do postaci iloczynowej typu \((x^2-4)(3x-2)=0\) oraz otrzymasz przynajmniej jedno poprawne rozwiązanie.
3 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Aby rozwiązać to równanie, najprościej będzie skorzystać z metody grupowania. Całość obliczeń będzie wyglądać następująco:
$$3x^3-2x^2-12x+8=0 \\
x^2\cdot(3x-2)-4\cdot(3x-2)=0 \\
(x^2-4)\cdot(3x-2)=0$$
Aby powyższe równanie było równe \(0\), to wartość któregoś z tych nawiasów musi być równa \(0\), zatem:
$$x^2-4=0 \quad\lor\quad 3x-2=0 \\
x^2=4 \quad\lor\quad 3x=2 \\
x=2 \quad\lor\quad x=-2 \quad\lor\quad x=\frac{2}{3}$$
Zadanie 10. (1pkt) Na rysunku przedstawiono interpretację geometryczną w kartezjańskim układzie współrzędnych \((x,y)\) jednego z niżej zapisanych układów równań A-D.
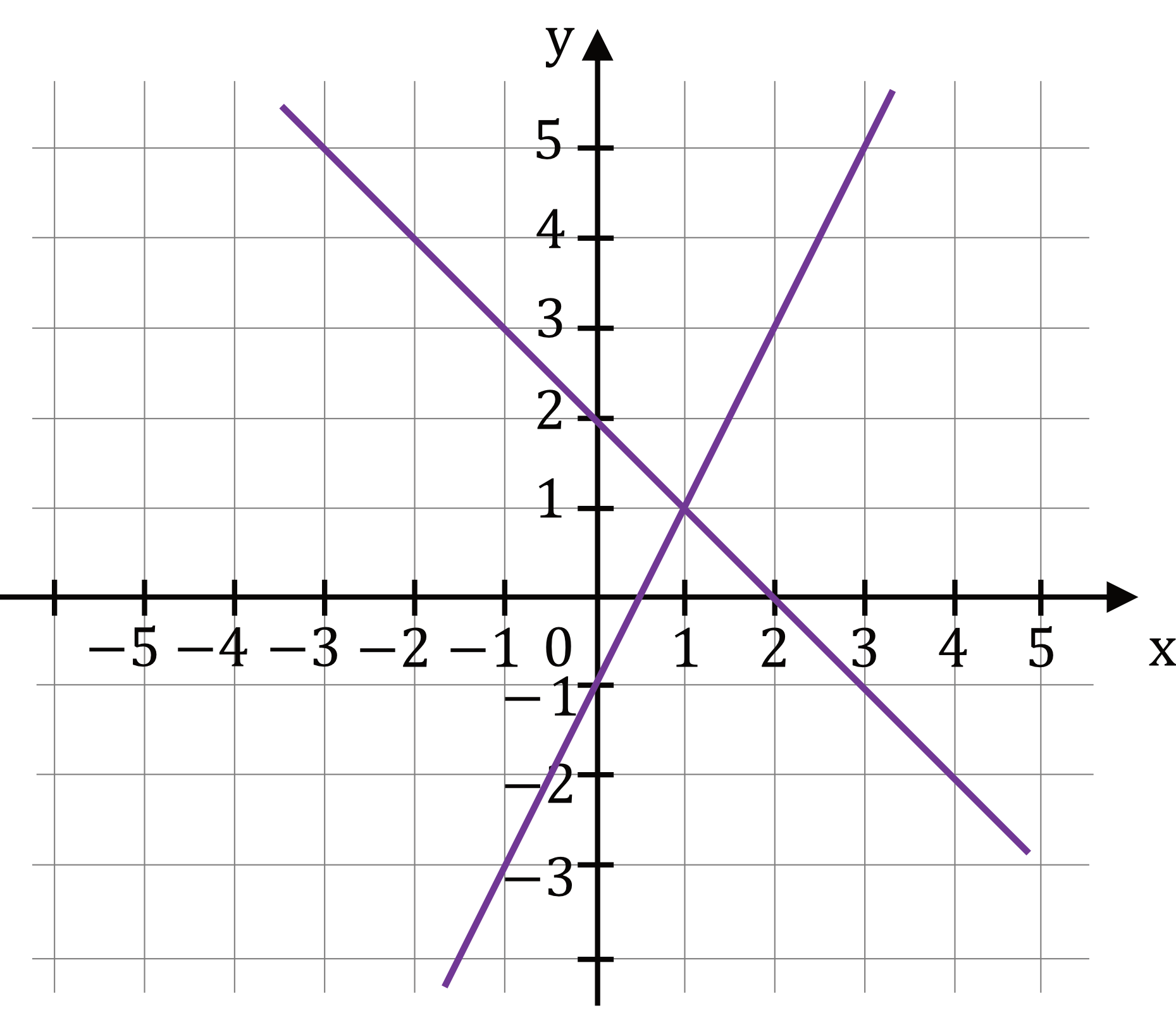
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest:
Zadanie 11. (2pkt) Dany jest prostokąt o bokach długości \(a\) i \(b\), gdzie \(a\gt b\). Obwód tego prostokąta jest równy \(30\). Jeden z boków prostokąta jest o \(5\) krótszy od drugiego.
Uzupełnij zdanie. Wybierz dwie właściwe odpowiedzi spośród oznaczonych literami A-F i wpisz te litery w wykropkowanych miejscach.
Zależności między długościami boków tego prostokąta zapisano w układach równań oznaczonych literami:
$$...... \text{oraz} ......$$
A. \(\begin{cases}
2ab=30 \\
a-b=5
\end{cases}\)
B. \(\begin{cases}
2a+b=30 \\
a=5b
\end{cases}\)
C. \(\begin{cases}
2(a+b)=30 \\
b=a-5
\end{cases}\)
D. \(\begin{cases}
2a+2b=30 \\
b=5a
\end{cases}\)
E. \(\begin{cases}
2a+2b=30 \\
a-b=5
\end{cases}\)
F. \(\begin{cases}
a+b=30 \\
a=b+5
\end{cases}\)
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie:
Krok 1. Zapisanie pierwszego równania.
Pierwsze równanie związane jest z obwodem prostokąta. Wiemy, że nasz prostokąt ma obwód równy \(30\). Na ten obwód będą składać się dwa boki o długości \(a\) oraz dwa boki o długości \(b\), zatem pierwszym równaniem jakie możemy ułożyć będzie:
$$2a+2b=30$$
I tu od razu możemy zapisać drugi wariant tego równania (który pojawi się jako alternatywna odpowiedź). Wyciągając dwójkę przed nawias, moglibyśmy zapisać, że:
$$2\cdot(a+b)=30$$
Krok 2. Zapisanie drugiego równania.
Drugie równanie wynika z informacji, że jeden z boków prostokąta jest o \(5\) krótszy od drugiego. Moglibyśmy zapisać, że w takim razie:
$$b=a-5$$
Przekształcając to równanie moglibyśmy otrzymać postać:
$$b+5=a \\
a-b=5$$
Krok 3. Wybór poprawnych odpowiedzi.
Analizując teraz dostępne odpowiedzi widzimy, że pasuje nam na pewno układ równań z odpowiedzi C oraz z odpowiedzi E.
Zadanie 12. (3pkt) W kartezjańskim układzie współrzędnych \((x,y)\) narysowano wykres funkcji \(y=f(x)\) (zobacz rysunek)
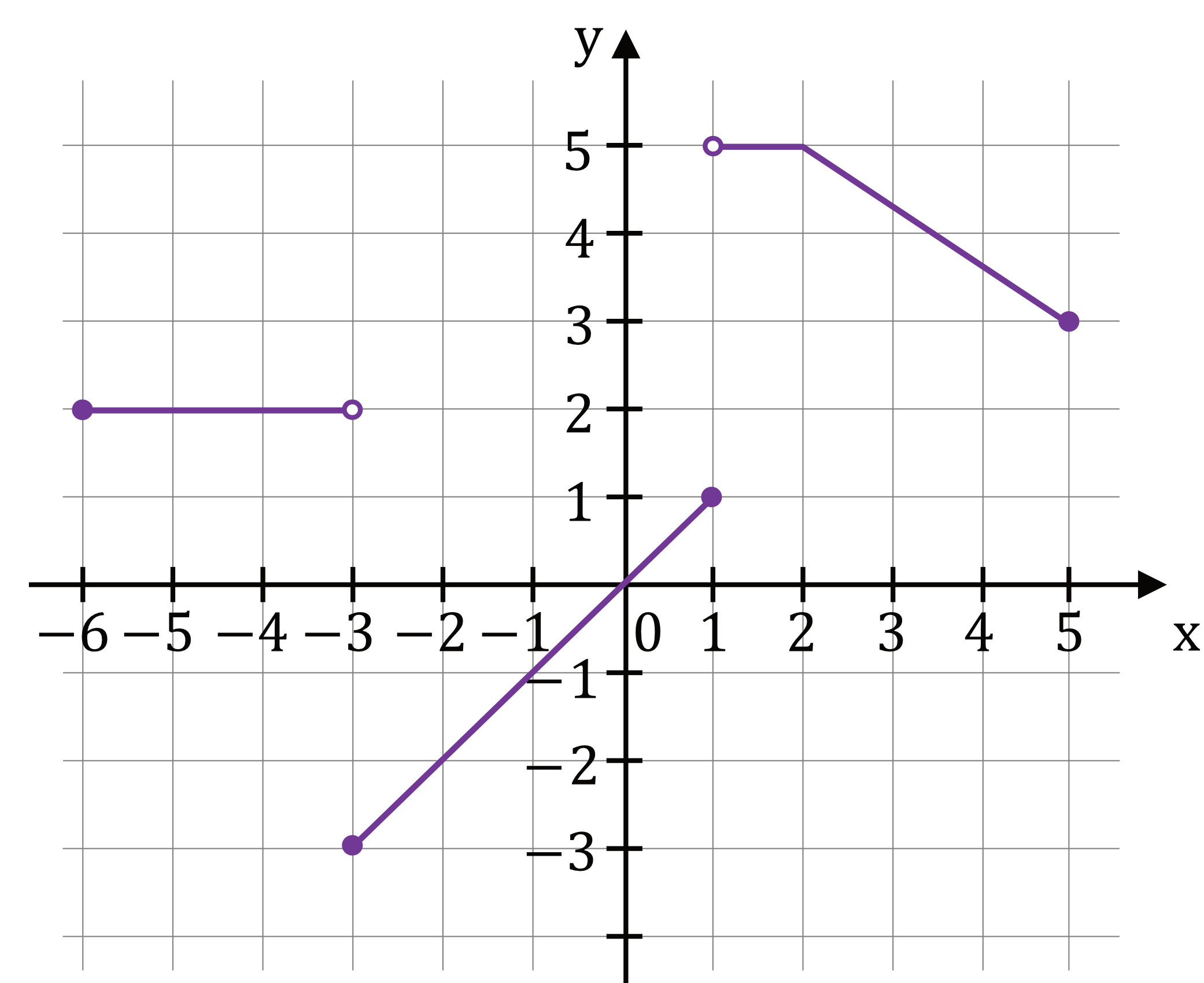
Zadanie 12.1. Dziedziną funkcji \(f\) jest zbiór:
Zadanie 12.2. Największa wartość funkcji \(f\) w przedziale \(\langle-4;1\rangle\) jest równa:
Zadanie 12.3. Funkcja \(f\) jest malejąca w zbiorze:
Zadanie 13. (1pkt) Funkcja liniowa \(f\) jest określona wzorem \(f(x)=ax+b\), gdzie \(a\) i \(b\) są pewnymi liczbami rzeczywistymi. Na 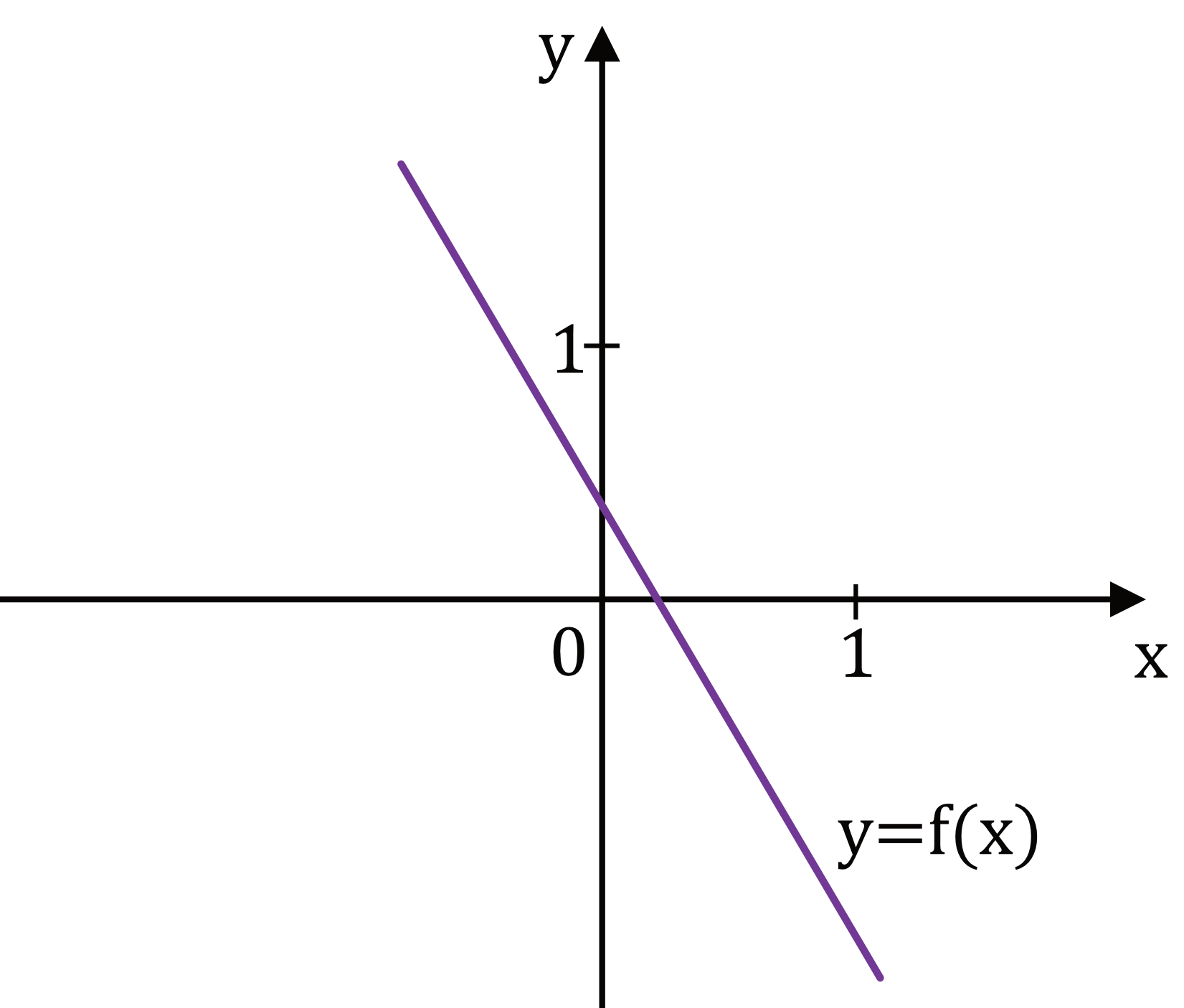
Liczba \(a\) oraz \(b\) we wzorze funkcji \(f\) spełniają warunki:
Zadanie 14. (1pkt) Jednym z miejsc zerowych funkcji kwadratowej \(f\) jest liczba \((-5)\). Pierwsza współrzędna wierzchołka paraboli, będącej wykresem funkcji \(f\) jest równa \(3\). Drugim miejscem zerowym funkcji \(f\) jest liczba:
Zadanie 15. (1pkt) Ciąg \((a_{n})\) jest określony wzorem \(a_{n}=2^n\cdot(n+1)\) dla każdej liczby naturalnej \(n\ge1\). Wyraz \(a_{4}\) jest równy:
Zadanie 16. (1pkt) Trzywyrazowy ciąg \((27, 9, a-1)\) jest geometryczny. Liczba \(a\) jest równa:
Zadanie 17. (2pkt) Pan Stanisław spłacił pożyczkę w wysokości \(8910 zł\) w osiemnastu ratach. Każda kolejna rata była mniejsza od poprzedniej o \(30 zł\). Oblicz kwotę pierwszej raty. Zapisz obliczenia.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy zapiszesz jakiekolwiek równanie wynikające z własności ciągów arytmetycznych, w którym jedyną niewiadomą jest \(a_{1}\).
ALBO
• Gdy zapiszesz układ równań z dwoma niewiadomymi.
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Opisaną w zadaniu sytuację możemy przedstawić jako ciąg arytmetyczny, w którym \(S_{n}=8910\), \(n=18\) oraz \(r=-30\). Poszukiwaną wartością jest \(a_{1}\).
W zadaniu możemy więc skorzystać ze wzoru na sumę \(n\)-początkowych wyrazów ciągu arytmetycznego, czyli:
$$S_{n}=\frac{2a_{1}+(n-1)r}{2}\cdot n$$
Podstawiając teraz znane dane, otrzymamy:
$$8910=\frac{2a_{1}+(18-1)\cdot(-30)}{2}\cdot18 \\
8910=\frac{2a_{1}+17\cdot(-30)}{2}\cdot18 \\
8910=\frac{2a_{1}-510}{2}\cdot18 \\
495=\frac{2a_{1}-510}{2} \\
990=2a_{1}-510 \\
2a_{1}=1500 \\
a_{1}=750$$
Zadanie 18. (1pkt) W kartezjańskim układzie współrzędnych \((x,y)\) zaznaczono kąt \(\alpha\) o wierzchołku w punkcie \(O=(0;0)\). Jedno z ramion tego kąta pokrywa się z dodatnią półosią \(Ox\), a drugie przechodzi przez punkt \(P=(-3;1)\) (zobacz rysunek).
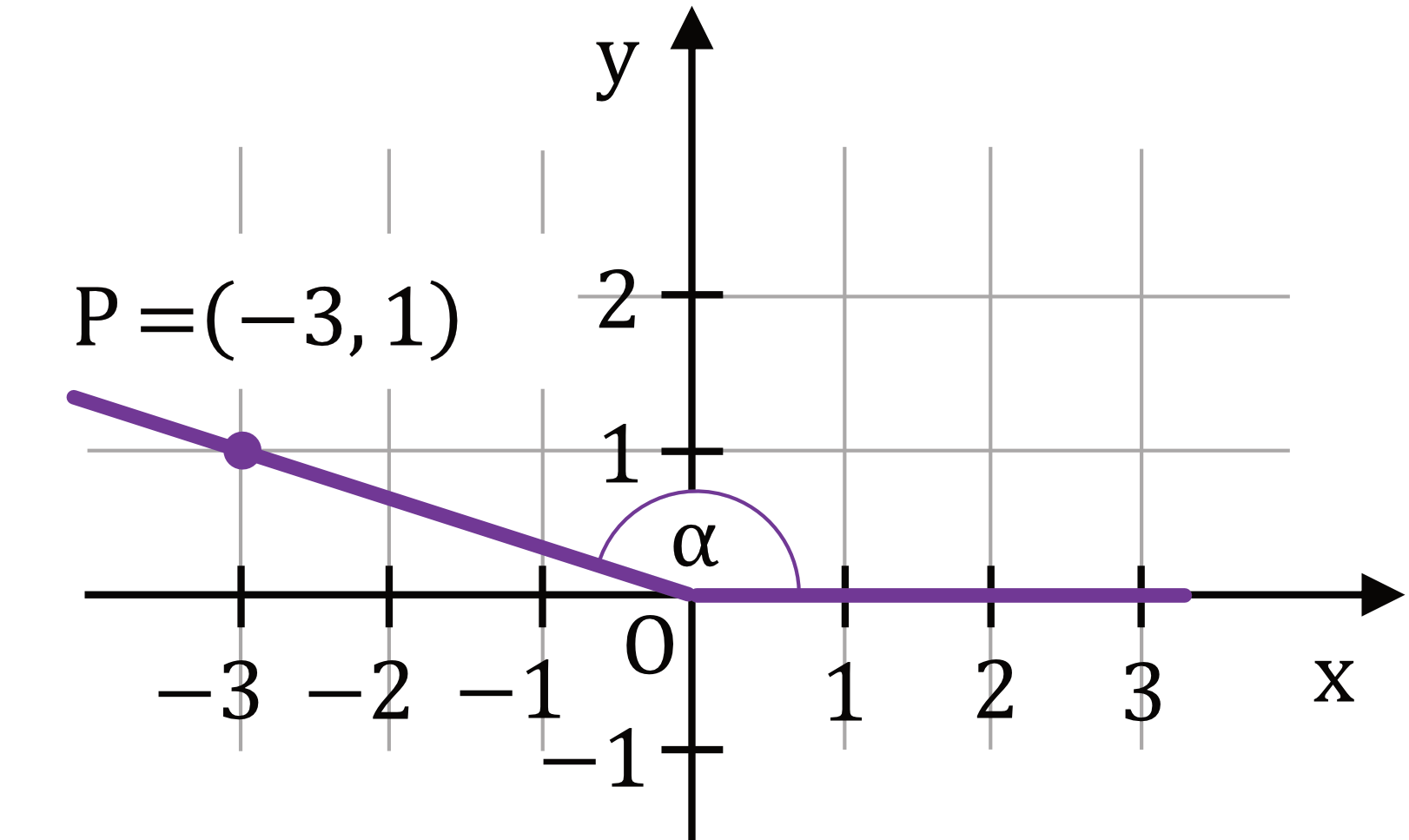
Tangens kąta \(\alpha\) jest równy:
Zadanie 19. (1pkt) Dla każdego kąta ostrego \(\alpha\) wyrażenie \(sin^4\alpha+sin^2\alpha\cdot cos^2\alpha\) jest równe:
Zadanie 20. (1pkt) W rombie o boku długości \(6\sqrt{2}\) kąt rozwarty ma miarę \(150°\). Iloczyn długości przekątnych tego rombu jest równy:
Zadanie 21. (1pkt) Punkty \(A\), \(B\), \(C\) leżą na okręgu o środku w punkcie \(O\). Kąt \(ACO\) ma miarę \(70°\) (zobacz rysunek).
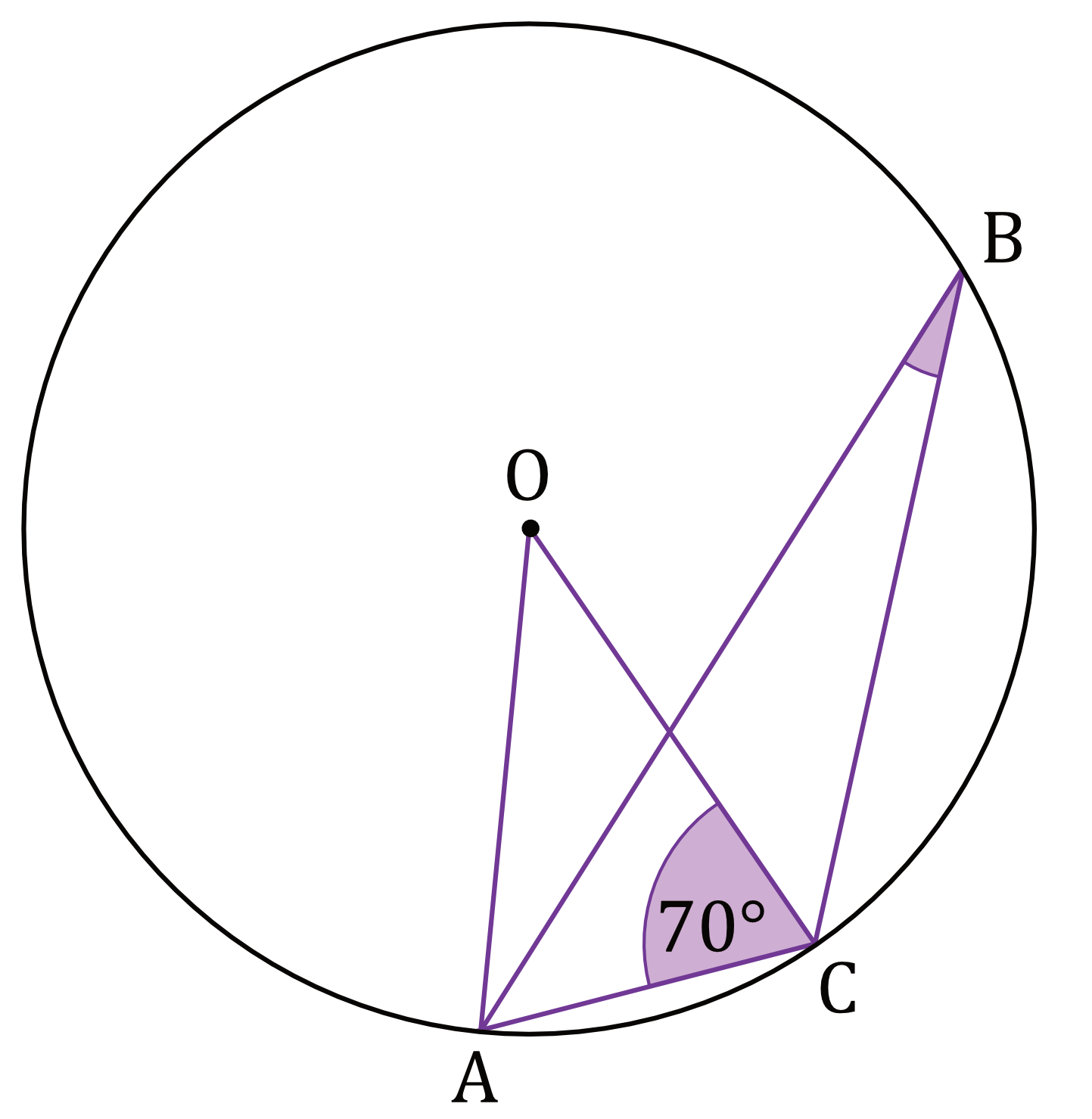
Miara kąta ostrego \(ABC\) jest równa:
Zadanie 22. (2pkt) Trójkąty prostokątne \(T_{1}\) i \(T_{2}\) są podobne. Przyprostokątne trójkąta \(T_{1}\) mają długości \(5\) i \(12\). Przeciwprostokątna trójkąta \(T_{2}\) ma długość \(26\). Oblicz pole trójkąta \(T_{2}\). Zapisz obliczenia.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz skalę podobieństwa (patrz: Krok 2.).
ALBO
• Gdy obliczysz, że przyprostokątne trójkąta \(T_{2}\) mają długość \(10\) i \(24\).
ALBO
• Gdy obliczysz długość przeciwprostokątnej (patrz: Krok 1.) i zapiszesz równanie na stosunek pól powierzchni typu \(\frac{P_{1}}{P_{2}}=\left(\frac{|BC|}{26}\right)^2\).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Obliczenie długości przeciwprostokątnej trójkąta \(T_{1}\).
Z treści zadania wynika, że trójkąt \(T_{1}\) ma przyprostokątne o długości \(5\) i \(12\), zatem korzystając z twierdzenia Pitagorasa możemy obliczyć długość przeciwprostokątnej:
$$5^2+12^2=c^2 \\
25+144=c^2 \\
c^2=169 \\
c=13 \quad\lor\quad c=-13$$
Ujemną wartość oczywiście odrzucamy, bo długość boku jest dodatnia, zatem zostaje nam \(c=13\).
Krok 2. Obliczenie skali podobieństwa.
Z treści zadania wynika, że drugi trójkąt \(T_{2}\) ma przeciwprostokątną o długości \(26\), czyli ma przeciwprostokątną dwa razy dłuższą od trójkąta \(T_{1}\).

To oznacza, że skala podobieństwa tych trójkątów wynosi \(k=2\).
Krok 3. Obliczenie pola powierzchni trójkąta \(T_{2}\).
Obliczmy najpierw pole trójkąta \(T_{1}\). Korzystając ze wzoru na pole trójkąta, możemy zapisać, że:
$$P=\frac{1}{2}\cdot12\cdot5 \\
P=30$$
Zgodnie z własnościami trójkątów podobnych, jeśli skala podobieństwa figur jest równa \(k\) to pole powierzchni figury podobnej będzie \(k^2\) razy większe. W naszym przypadku oznaczałoby to, że pole trójkąta \(T_{2}\) będzie \(4\) razy większe od pola trójkąta \(T_{1}\), zatem:
$$P=4\cdot30 \\
P=120$$
Zadanie 23. (1pkt) W kartezjańskim układzie współrzędnych \((x,y)\) dane są proste \(k\) oraz \(l\) o równaniach
$$k:\quad y=\frac{2}{3}x \\
l:\quad y=-\frac{3}{2}x+13$$
Proste \(k\) oraz \(l\):
i przecinają się w punkcie \(P\) o współrzędnych
Zadanie 24. (1pkt) W kartezjańskim układzie współrzędnych \((x,y)\) dana jest prosta \(k\) o równaniu \(y=-\frac{1}{3}x+2\).
Prosta o równaniu \(y=ax+b\) jest równoległa do prostej \(k\) i przechodzi przez punkt \(P=(3;5)\), gdy:
Zadanie 25. (1pkt) Dany jest graniastosłup prawidłowy czworokątny, w którym krawędź podstawy ma długość \(15\). Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem \(\alpha\) takim, że \(cos\alpha=\frac{\sqrt{2}}{3}\).
Długość przekątnej tego graniastosłupa jest równa:
Zadanie 26. (4pkt) Dany jest ostrosłup prawidłowy czworokątny. Wysokość ściany bocznej tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem \(30°\) i ma długość równą \(6\) (zobacz rysunek).
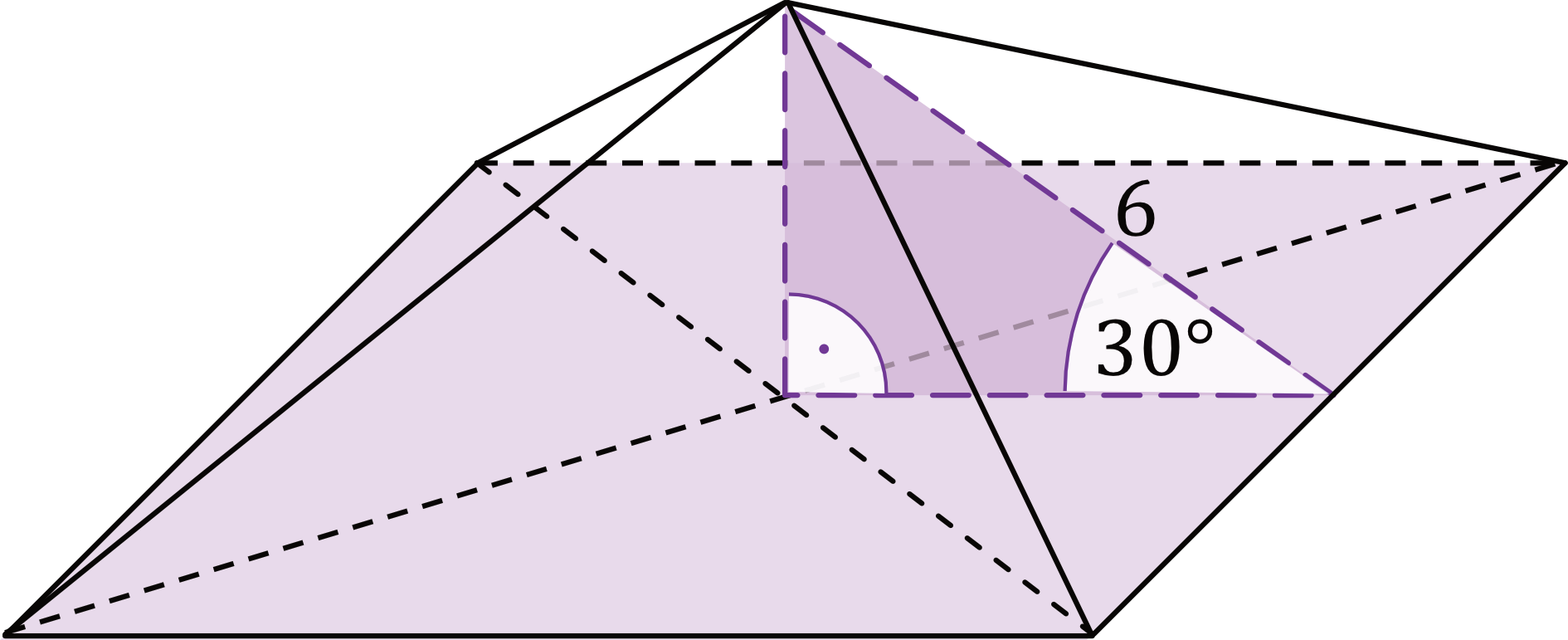
Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa. Zapisz obliczenia.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz wysokość ostrosłupa (patrz: Krok 1.).
ALBO
• Gdy obliczysz długość krawędzi podstawy (patrz: Krok 2.).
2 pkt
• Gdy obliczysz wysokość ostrosłupa (patrz: Krok 1.) oraz długość krawędzi podstawy (patrz: Krok 2.).
ALBO
• Gdy obliczysz tylko pole powierzchni całkowitej (patrz: Krok 5.).
3 pkt
• Gdy obliczysz tylko objętość ostrosłupa (patrz: Krok 4.).
ALBO
• Gdy obliczysz wysokość ostrosłupa (patrz: Krok 1.) oraz pole powierzchni całkowitej (patrz: Krok 5.).
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Obliczenie wysokości ostrosłupa.
Spójrzmy na trójkąt prostokątny, który został narysowany w treści zadania. Jest to klasyczny trójkąt o kątach \(30°, 60°, 90°\). Z własności tego trójkąta wynika, że krótsza przyprostokątna (którą w tym przypadku jest wysokość ostrosłupa) będzie dwa razy krótsza od przeciwprostokątnej. Tym samym możemy zapisać, że:
$$H=6:2 \\
H=3$$
Do tego samego wyniku dojdziemy korzystając z funkcji trygonometrycznej - w tej sytuacji sprawdzi się sinus:
$$sin30°=\frac{H}{6} \\
\frac{1}{2}=\frac{H}{6} \\
H=3$$
Krok 2. Obliczenie długości krawędzi podstawy.
Spójrzmy jeszcze raz na nasz trójkąt o kątach \(30°, 60°, 90°\). Z własności tego trójkąta wynika to, że jego dolna (dłuższa) przyprostokątna będzie \(\sqrt{3}\) razy dłuższa od krótszej przyprostokątnej, czyli moglibyśmy zapisać, że ta dolna przyprostokątna ma długość \(x=3\sqrt{3}\).
W podstawie ostrosłupa znajduje się kwadrat (wiemy to, ponieważ ostrosłup jest prawidłowy czworokątny). Ta dolna przyprostokątna naszego analizowanego przed chwilą trójkąta będzie więc połową długości boku kwadratu. To oznacza, że w takim razie:
$$a=2\cdot3\sqrt{3} \\
a=6\sqrt{3}$$
Krok 3. Obliczenie pola podstawy oraz pola powierzchni bocznej.
W podstawie naszej bryły mamy kwadrat o boku \(a=6\sqrt{3}\), zatem pole powierzchni podstawy będzie równe:
$$P_{p}=(6\sqrt{3})^2 \\
P_{p}=36\cdot3 \\
P_{p}=108$$
Ściany boczne naszej bryły to trójkąty o podstawie \(a=6\sqrt{3}\) oraz wysokości \(h=6\). Mamy cztery takie ściany, więc pole powierzchni bocznej będzie równe:
$$P_{b}=4\cdot\frac{1}{2}\cdot6\sqrt{3}\cdot6 \\
P_{b}=72\sqrt{3}$$
Krok 4. Obliczenie objętości ostrosłupa.
Znając pole podstawy oraz wysokość ostrosłupa, możemy zapisać, że:
$$V=\frac{1}{3}\cdot P_{p}\cdot H \\
V=\frac{1}{3}\cdot108\cdot3 \\
V=108$$
Krok 5. Obliczenie pola powierzchni całkowitej.
Znając pole podstawy oraz pole powierzchni bocznej, możemy zapisać, że:
$$P_{c}=P_{p}+P_{b} \\
P_{c}=108+72\sqrt{3}$$
Zadanie 27. (1pkt) W pewnym ostrosłupie prawidłowym stosunek liczby \(W\) wszystkich wierzchołków do liczby \(K\) wszystkich krawędzi jest równy \(\frac{W}{K}=\frac{3}{5}\). Podstawą tego ostrosłupa jest:
Zadanie 28. (1pkt) Wszystkich liczb naturalnych pięciocyfrowych, w których zapisie dziesiętnym występują tylko cyfry \(0,5,7\) (np. \(57075\), \(55555\)) jest:
Zadanie 29. (2pkt) Na diagramie poniżej przedstawiono ceny pomidorów w szesnastu wybranych sklepach.
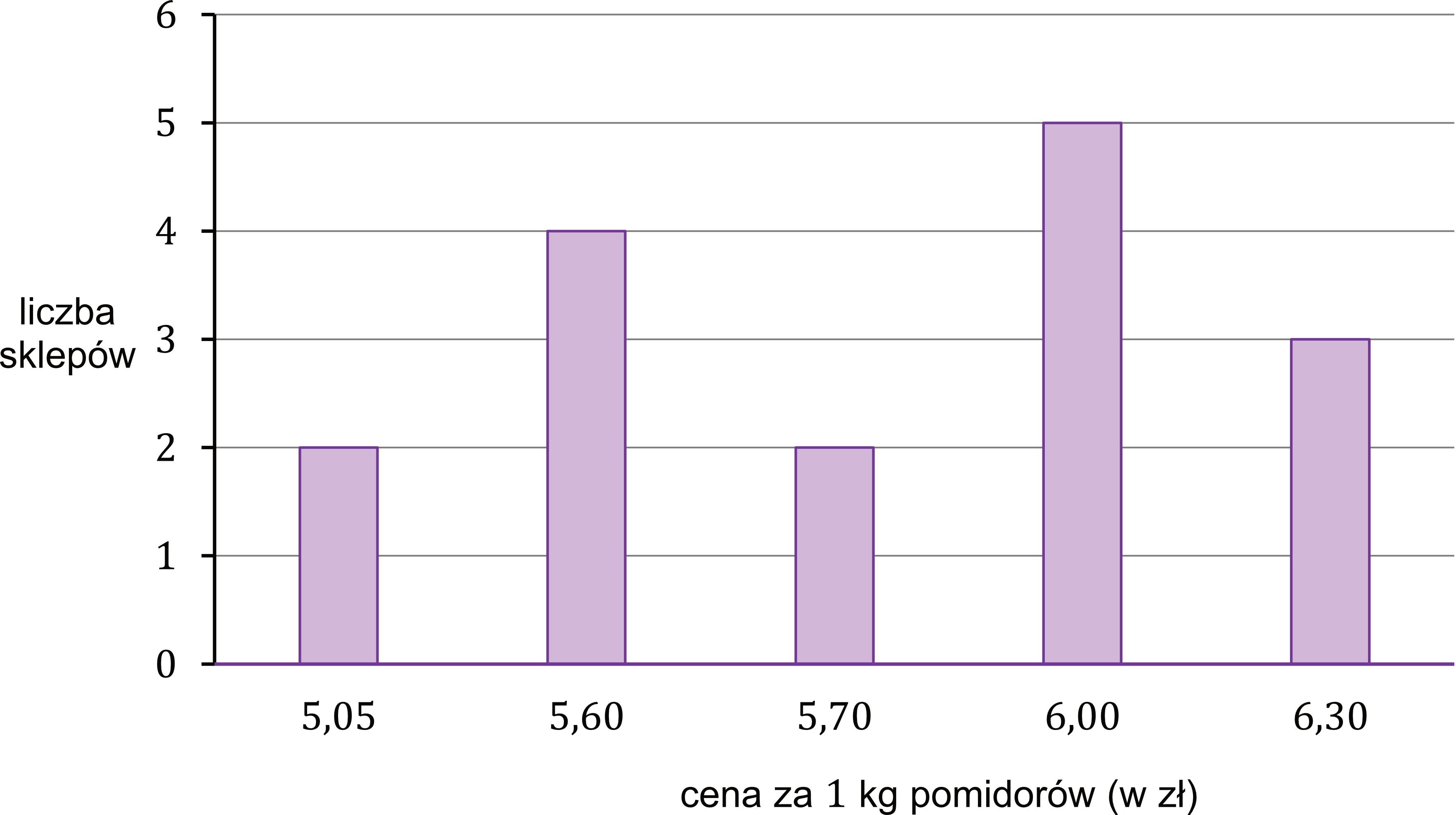
Uzupełnij tabelę. Wpisz w każdą pustą komórkę tabeli właściwą odpowiedź, wybraną spośród oznaczonych literami A–E.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie:
Krok 1. Obliczenie mediany ceny kilograma pomidorów.
Zebrano ceny pomidorów z \(16\) sklepów, czyli liczba wyników jest parzysta. To oznacza, że mediana będzie średnią arytmetyczną między środkowymi wyrazami - czyli w naszym przypadku będzie to średnia arytmetyczna ósmego i dziewiątego wyniku.
Wyliczając medianę musimy uporządkować liczby w porządku niemalejącym (czyli od najmniejszych do największych). Jeśli chcemy, to moglibyśmy wypisać te ceny jako ciąg:
$$5,05; \; 5,05; \; 5,60; \; 5,60...$$
Analizując wykres i pojawiające się tam ceny wynika, że ósmą w kolejności ceną byłoby \(5,70\), a dziewiątą byłoby już \(6,00\). To oznacza, że mediana będzie równa:
$$m=\frac{5,70+6,00}{2} \\
m=\frac{11,70}{2} \\
m=5,85$$
Krok 2. Obliczenie średniej ceny kilograma pomidorów.
Średnią cenę obliczymy w następujący sposób:
$$śr=\frac{2\cdot5,05+4\cdot5,60+2\cdot5,70+5\cdot6,00+3\cdot6,30}{16} \\
śr=\frac{10,10+22,40+11,40+30+18,90}{16} \\
śr=\frac{92,80}{16} \\
śr=5,80$$
Zadanie 30. (2pkt) Ze zbioru ośmiu liczb \({2,3,4,5,6,7,8,9}\) losujemy ze zwracaniem kolejno dwa razy po jednej liczbie.
Oblicz prawdopodobieństwo zdarzenia \(A\) polegającego na tym, że iloczyn wylosowanych liczb jest podzielny przez \(15\). Zapisz obliczenia.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz liczbę wszystkich zdarzeń elementarnych (patrz: Krok 1.).
ALBO
• Gdy obliczysz liczbę wszystkich zdarzeń sprzyjających (patrz: Krok 2.).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Obliczenie liczby wszystkich zdarzeń elementarnych.
Mamy \(8\), a losowanie odbywa się ze zwracaniem, czyli za pierwszym razem możemy wylosować jedną z ośmiu liczb i za drugim razem też możemy wylosować jedną z ośmiu liczb. To oznacza, że zgodnie z regułą mnożenia liczba zdarzeń elementarnych będzie równa \(|Ω|=8\cdot8=64\).
Krok 2. Obliczenie liczby zdarzeń sprzyjających.
Zdarzeniem sprzyjającym jest sytuacja w której wylosowane liczby pomnożone przez siebie dadzą wynik podzielny przez \(15\), czyli dadzą wynik równy \(15, 30, 45, 60, 75\) (większej liczby nie będziemy w stanie osiągnąć). Skoro tak, to pasującymi zdarzeniami będą:
$$(3,5); (5,3), (5,6); (6,5), (5,9); (9,5)$$
To oznacza, że \(|A|=6\).
Krok 3. Obliczenie prawdopodobieństwa.
$$P(A)=\frac{|A|}{|Ω|}=\frac{6}{64}=\frac{3}{32}$$
Zadanie 31. (3pkt) Właściciel pewnej apteki przeanalizował dane dotyczące liczby obsługiwanych klientów z \(30\) kolejnych dni. Przyjmijmy, że liczbę \(L\) obsługiwanych klientów \(n\)-tego dnia opisuje funkcja:
$$L(n)=-n^2+22n+279$$
gdzie \(n\) jest liczbą naturalną spełniającą warunki \(n\ge1\) i \(n\le30\).
Zadanie 31.1. Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F - jeśli jest fałszywe.
Łączna liczba klientów obsłużonych w czasie wszystkich analizowanych dni jest równa \(L(30)\).
W trzecim dniu analizowanego okresu obsłużono \(336\) klientów.
Zadanie 31.2. Którego dnia analizowanego okresu w aptece obsłużono największą liczbę klientów? Oblicz liczbę klientów obsłużonych tego dnia. Zapisz obliczenia.
Przyznaj sobie samodzielnie punkty, zgodnie z proponowaną punktacją
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz którego dnia było najwięcej klientów (patrz: Krok 1.).
ALBO
• Gdy obliczysz liczbę klientów (patrz: Krok 2.).
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Wyjaśnienie:
Krok 1. Wyznaczenie dnia, w którym było najwięcej klientów.
Liczba obsługiwanych klientów jest opisana funkcją kwadratową. Wiemy, że wykresem funkcji kwadratowej jest parabola, która w tym przypadku będzie miała ramiona skierowane do dołu, bo współczynnik \(a=-1\). To oznacza, że swoją największą wartość ta funkcja będzie przyjmowała w wierzchołku.
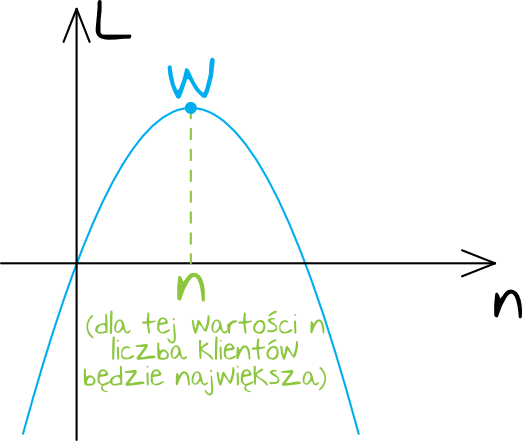
Chcąc się dowiedzieć, którego dnia było najwięcej klientów, wystarczy obliczyć tzw. pierwszą współrzędną wierzchołka (zwyczajowo opisywaną jako \(p\)). Skorzystamy ze wzoru:
$$p=\frac{-b}{2a}$$
Ze wzoru \(L(n)=-n^2+22n+279\) odczytujemy, że współczynniki \(a=-1\) oraz \(b=22\), zatem:
$$p=\frac{-b}{2a} \\
p=\frac{-22}{2\cdot(-1)} \\
p=\frac{-22}{-2} \\
p=11$$
Krok 2. Wyznaczenie liczby klientów jedenastego dnia.
Liczbę klientów jedenastego dnia możemy obliczyć wyznaczając \(q\) (chcąc tak postąpić wystarczy skorzystać ze wzoru \(q=\frac{-Δ}{4a}\) lub też obliczając po prostu \(L(11)\). Wybierzmy może ten drugi sposób. Podstawiając \(n=11\) do wzoru funkcji, otrzymamy:
$$L(11)=-(11)^2+22\cdot11+279 \\
L(11)=-121+242+279 \\
L(11)=400$$