Przed Tobą sprawdzian z matematyki, który sprawdzi Twoją wiedzę z działu: Funkcja wykładnicza. W teście znajduje się 10 zadań, a każde z nich jest warte 1 punkt. Całość powinna Ci zająć około 15 minut. Po zakończeniu sprawdzianu możesz przejrzeć swoje odpowiedzi wraz z pełnymi rozwiązaniami do zadań. Życzę powodzenia!
Zadanie 1. (1pkt) Funkcja \(f(x)=a^x\) przechodzi przez punkt \(P=(3;8)\) dla:
Zadanie 2. (1pkt) Wykres funkcji wykładniczej \(f(x)=a^x\):
Zadanie 3. (1pkt) 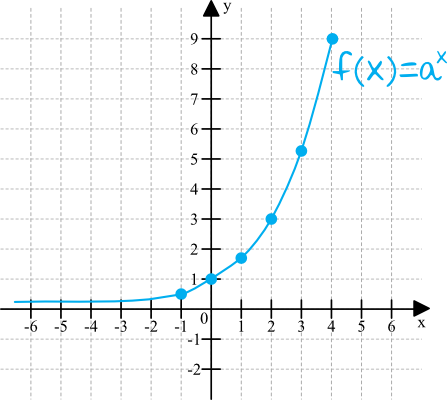
Wzorem powyższej funkcji wykładniczej \(f(x)=a^x\) jest:
Zadanie 4. (1pkt) Dana jest funkcja wykładnicza \(f(x)=a^x+2\). Dla każdego \(a\gt0\) funkcja ta będzie przechodzić przez punkt:
Zadanie 5. (1pkt) Rozwiązaniem równania \(5^x=\sqrt{0,2}\) jest:
Zadanie 6. (1pkt) Funkcja wykładnicza \(f(x)=\left(\frac{3}{2}\right)^x\) jest malejąca.
Zadanie 7. (1pkt) Dla ujemnych argumentów funkcja \(f(x)=\left(\frac{1}{2}\right)^x\) przyjmuje większą wartość niż funkcja \(g(x)=(\sqrt{2})^x\).
Zadanie 8. (1pkt) 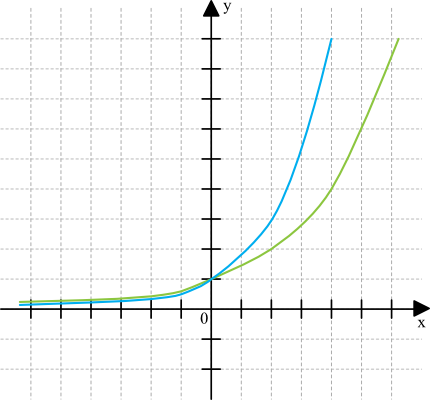
Dany jest następujący układ współrzędnych, bez podpisanych konkretnych wartości. Wiemy, że jedna z powyższych funkcji to \(f(x)=(\sqrt{2})^x\), a druga to \(g(x)=(\sqrt{3})^x\). Jaś twierdzi, że funkcja \(f(x)\) jest zaznaczona na niebiesko, a \(g(x)\) jest zaznaczona na zielono. Małgosia twierdzi inaczej - jej zdaniem funkcja \(f(x)\) jest zaznaczona na zielono, a \(g(x)\) na niebiesko. Kto ma rację?
Zadanie 9. (1pkt) Dla jakiego argumentu \(x\) funkcja wykładnicza \(f(x)=(0,25)^x\) przyjmuje wartość równą \(64\)?
Zadanie 10. (1pkt) Dana jest funkcja wykładnicza \(f(x)=4^x-m\). Dla jakiego parametru \(m\) funkcja ta ma miejsce zerowe równe \(2\)?