Przed Tobą sprawdzian z matematyki, który sprawdzi Twoją wiedzę z działu: Trygonometria w trójkącie prostokątnym. W teście znajduje się 10 zadań, a każde z nich jest warte 1 punkt. Całość powinna Ci zająć około 15 minut. Po zakończeniu sprawdzianu możesz przejrzeć swoje odpowiedzi wraz z pełnymi rozwiązaniami do zadań. Życzę powodzenia!
Zadanie 1. (1pkt)  Trójkąt 6-8-x
Trójkąt 6-8-x
Czy jesteśmy w stanie obliczyć sinus kąta \(α\)?
Zadanie 2. (1pkt) Która z tych wartości jest największa?
Zadanie 3. (1pkt) Tylko jedna z poniższych liczb może być wartością sinusa kąta ostrego. Która?
Zadanie 4. (1pkt) 
Jeżeli \(tgα=\frac{3}{4}\), to pole tego trójkąta jest równe:
Zadanie 5. (1pkt) W trójkącie prostokątnym jedna przyprostokątna jest \(3\) razy dłuższa od drugiej. Jeżeli kąt \(α\) jest kątem leżącym przy krótszej przyprostokątnej, to:
Zadanie 6. (1pkt) 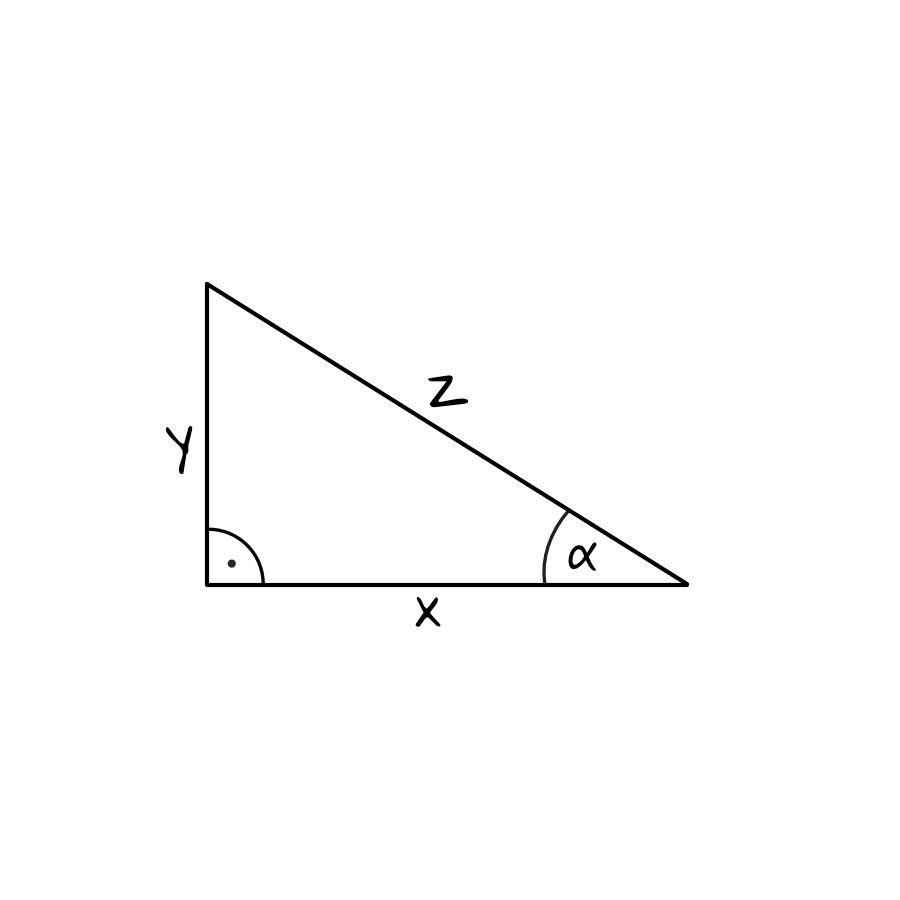
Wiemy, że \(sinα=\frac{5}{8}\). W związku z tym na pewno \(x=5\) oraz \(z=8\).
Zadanie 7. (1pkt) 
W tym trójkącie długość boku \(a\) jest równa nieco ponad \(4,5\).
Zadanie 8. (1pkt) Wiemy, że \(cosα=0,8\). Jaś po spojrzeniu w tablice trygonometryczne stwierdził, że w takim razie kąt \(α\) jest równy w przybliżeniu \(37°\), ale tak będąc bardziej precyzyjnym to według Jasia jest to kąt trochę większy niż \(37°\). Małgosia uważa, że faktycznie w przybliżeniu będzie to kąt \(37°\), ale jej zdaniem realnie ta wartość jest trochę mniejsza niż \(37°\). Kto ma rację?
Zadanie 9. (1pkt) W trójkącie prostokątnym jeden z kątów ostrych ma miarę \(α\). Przez ten kąt poprowadzono dwusieczną tego kąta, otrzymując w ten sposób dwa kąty \(β\). W tej sytuacji możemy powiedzieć, że na pewno:
Zadanie 10. (1pkt) W dwupoziomowym sklepie w galerii handlowej zamontowano ruchome schody. Odległość między podłogą na parterze i podłogą na pierwszym piętrze wynosi \(5\) metrów. Jaka jest długość schodów, jeżeli nachylone są one do podłogi pod kątem \(35°\)?