Przed Tobą sprawdzian z matematyki, który sprawdzi Twoją wiedzę z działu: Koła i okręgi. W teście znajduje się 10 zadań, a każde z nich jest warte 1 punkt. Całość powinna Ci zająć około 15 minut. Po zakończeniu sprawdzianu możesz przejrzeć swoje odpowiedzi wraz z pełnymi rozwiązaniami do zadań. Życzę powodzenia!
Zadanie 1. (1pkt) Koło o średnicy \(6\) ma pole powierzchni równe:
Zadanie 2. (1pkt) 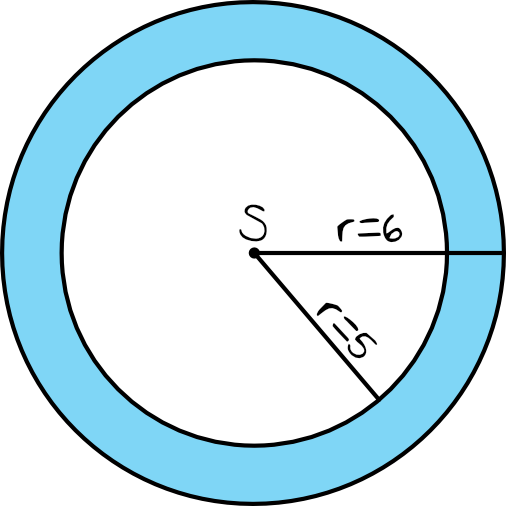
Pole powierzchni powyższego pierścienia jest równe:
Zadanie 3. (1pkt) Koła o polach \(4π\) oraz \(8π\) są styczne zewnętrznie. Odległość między środkami tych okręgów jest równa:
Zadanie 4. (1pkt) Okręgi o obwodach \(6π\) oraz \(10π\) są styczne wewnętrznie. Odległość między środkami tych okręgów jest równa:
Zadanie 5. (1pkt) Koło od roweru ma promień równy \(r=28cm\). Ile pełnych obrotów wykona to koło na trasie \(5km\)? Do obliczeń przyjmij przybliżenie \(π\approx3,14\).
Zadanie 6. (1pkt) 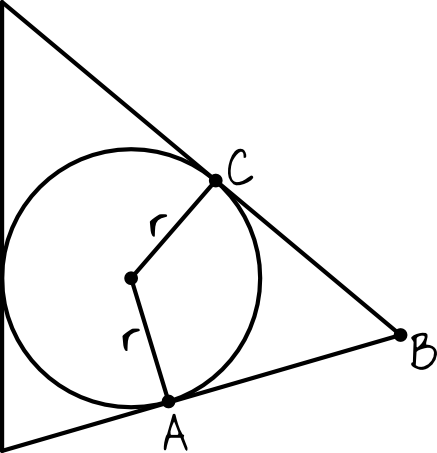
Na powyższym rysunku odcinek \(AB\) jest równy odcinkowi \(BC\).
Zadanie 7. (1pkt) 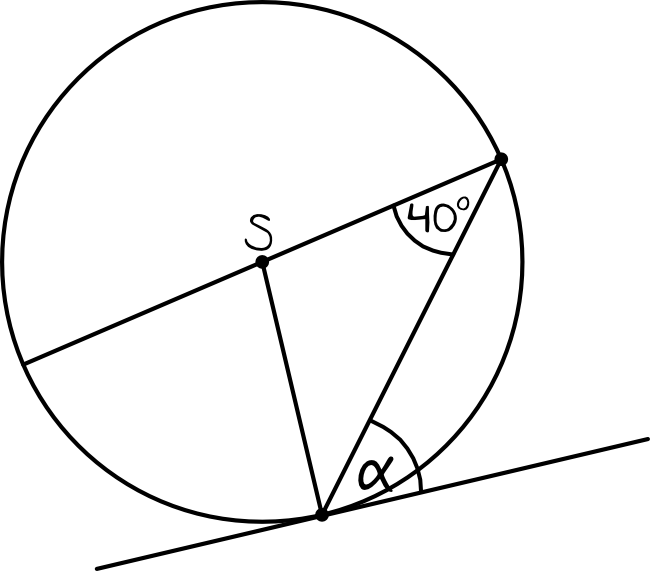
Kąt \(α\) zaznaczony na rysunku ma miarę 40°.
Zadanie 8. (1pkt) Dany jest okrąg o promieniu \(r=5\) i środku w punkcie \(S=(-3;4)\). Jaś twierdzi, że ten okrąg idealnie przechodzi przez początek układu współrzędnych. Małgosia uważa, że faktycznie rysując szkic tej sytuacji można odnieść takie wrażenie, ale w rzeczywistości brakuje ułamków milimetra by tak się stało i ten okrąg jednak nie będzie przechodził przez początek układu współrzędnych. Kto ma rację?
Zadanie 9. (1pkt) 
Pole powierzchni niebieskiego obszaru stanowi (do obliczeń przyjmij przybliżenie \(\pi=3,14\)):
Zadanie 10. (1pkt) 
Długość powyższego łuku jest równa: