Przed Tobą sprawdzian z matematyki, który sprawdzi Twoją wiedzę z działu: Ostrosłupy. W teście znajduje się 10 zadań, a każde z nich jest warte 1 punkt. Całość powinna Ci zająć około 15 minut. Po zakończeniu sprawdzianu możesz przejrzeć swoje odpowiedzi wraz z pełnymi rozwiązaniami do zadań. Życzę powodzenia!
Zadanie 1. (1pkt) 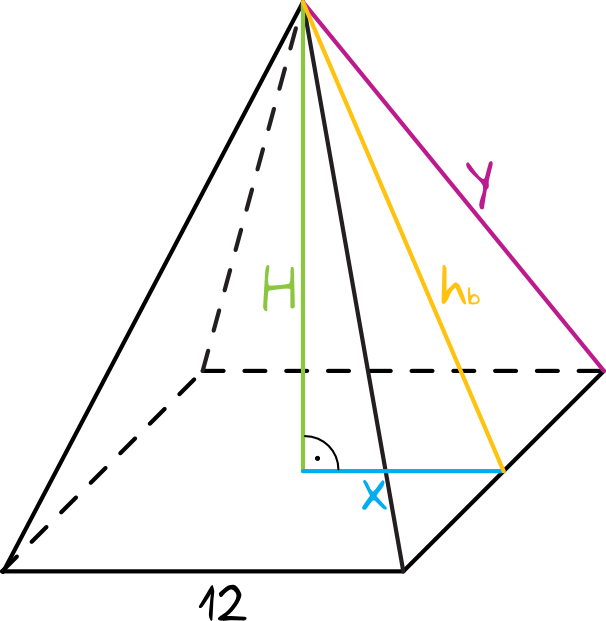
Jeżeli powyższy ostrosłup jest prawidłowy to na pewno:
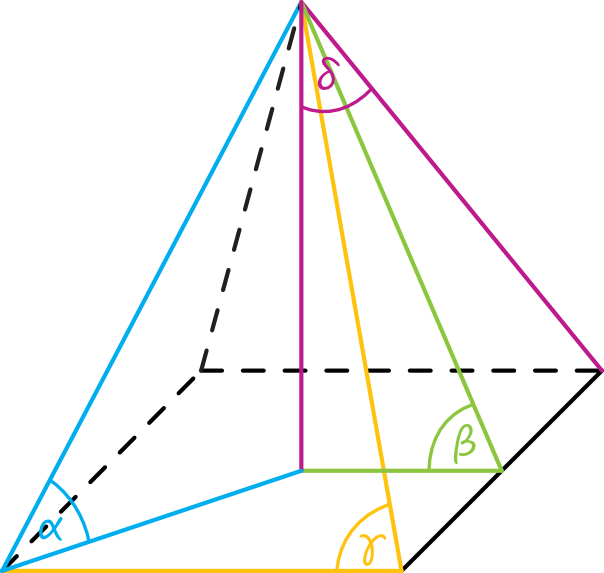
Zadanie 2. (1pkt) Kąt nachylenia ściany bocznej ostrosłupa do płaszczyzny podstawy to kąt:
Zadanie 3. (1pkt) Dany jest ostrosłup prawidłowy trójkątny w którym krawędź podstawy ma długość \(a=6\). Jeżeli objętość tej bryły jest równa \(36\sqrt{3}\), to wysokość ostrosłupa ma miarę:
Zadanie 4. (1pkt) W ostrosłupie prawidłowym czworokątnym krawędź boczna o długości \(6\) nachylona jest do płaszczyzny podstawy pod kątem \(30°\). Wysokość ostrosłupa jest równa:
Zadanie 5. (1pkt) Dany jest ostrosłup prawidłowy czworokątny w którym krawędzie podstawy mają długość \(4\), a krawędzie boczne mają długość \(6\). Kąt nachylenia krawędzi bocznej do podstawy ma miarę:
Zadanie 6. (1pkt) Dany jest ostrosłup prawidłowy trójkątny \(ABCD\) którego krawędzie podstawy mają długość \(a\).

Odcinek \(SC\) ma miarę \(\frac{1}{3}\cdot\frac{a\sqrt{3}}{2}\).
Zadanie 7. (1pkt) Ostrosłup może mieć \(99\) krawędzi.
Zadanie 8. (1pkt) Jaś twierdzi, że czworościan foremny to bryła, która ma w podstawie kwadrat, a w ścianach bocznych znajdują się trójkąty równoboczne. Małgosia uważa, że czworościan foremny to bryła w której wszystkie ściany są trójkątami równobocznymi. Kto ma rację?
Zadanie 9. (1pkt) Suma długości krawędzi ostrosłupa prawidłowego czworokątnego jest równa \(48\). Jeżeli krawędź boczna jest \(2\) razy dłuższa od krawędzi podstawy to wysokość ściany bocznej ma długość:
Zadanie 10. (1pkt) Gęstość złota wynosi \(19300kg/m^3\). Jeżeli poniższa piramidka wykonana jest w całości ze złota, to jej waga wynosi:


znowu pan mnie podszedł w ostatnim zadaniu
Staram się podpuszczać z tymi zadaniami jak tylko mogę :D
Test był bardzo dobrze skonstruowany, bardzo podobało mi się to, że z każdym zadaniem mogłem poczuć dreszczyk emocji związany z podnoszącym się poziomem trudności. Uświadczyło mnie to tylko w tym jaki beznadziejny jestem w dziedzinach matematycznych. Jednak, gdy w końcu się w tym utwierdziłem zaczynam nową przygodę z matematyką, bo pragnę poznać jej wszelkie tajniki, które pomogą zdać mi maturę na 101%. Bardzo dziękuję wszystkich zgromadzonym tutaj uczonym z zespołu Szalonych Liczb. Pozdrawiam cieplutko i uważajcie na drodze z racji na obecny teraz śnieg.