Funkcje trygonometryczne - zadania
Zadanie 7. (2pkt) Podstawy trapezu prostokątnego mają długości \(6\) i \(10\) oraz tangens kąta ostrego jest równy \(3\). Oblicz pole tego trapezu.
Wyjaśnienie:
Krok 1. Sporządzenie rysunku poglądowego.
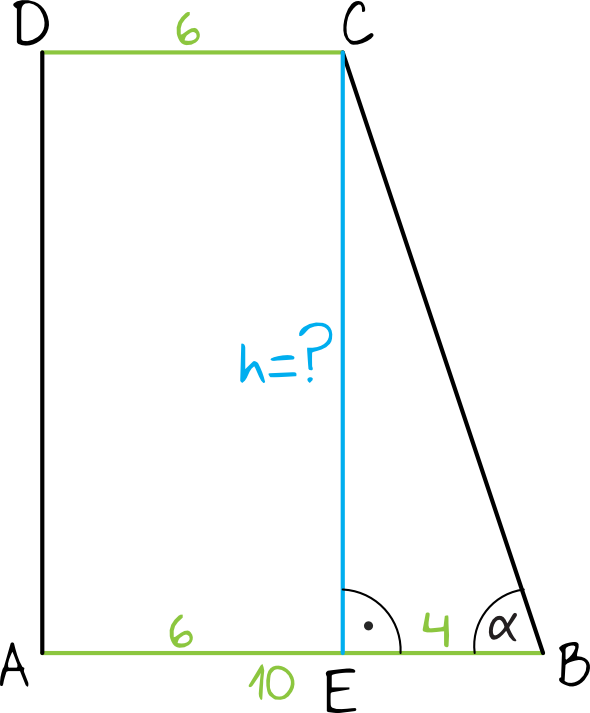
Krok 2. Obliczenie długości odcinków \(AE\) oraz \(EB\).
Długość odcinka \(AE\) jest identyczna co długość odcinka \(DC\), więc:
$$|AE|=|DC|=6$$
Długość odcinka \(EB\) jest różnicą między dłuższą i krótszą podstawą, więc:
$$|EB|=|AB|-|DC|=10-6=4$$
Krok 3. Obliczenie długości odcinka \(CE\).
Aby móc obliczyć pole trapezu potrzebna nam jest znajomość jego wysokości. Musimy więc poznać długość odcinka \(AD\) lub \(CE\). Długości odcinka \(AD\) nie mamy jak wyliczyć, natomiast \(CE\) jesteśmy w stanie wyznaczyć korzystając z tangensa kąta ostrego, który zgodnie z treścią zadania jest równy \(3\). Z definicji tangensa wiemy, że tangens to stosunek długości przyprostokątnej leżącej naprzeciw kąta \(α\) do długości przyprostokątnej leżącej przy tym kącie. Zatem:
$$tgα=\frac{|CE|}{|EB|} \\
3=\frac{|CE|}{4} \\
|CE|=12$$
To oznacza, że wysokość naszego trapezu jest równa \(12\).
Krok 4. Obliczenie pola trapezu.
$$P=\frac{1}{2}\cdot(a+b)\cdot h \\
P=\frac{1}{2}\cdot(6+10)\cdot12 \\
P=\frac{1}{2}\cdot16\cdot12 \\
P=8\cdot12 \\
P=96$$
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz wysokość trapezu, czyli \(h=12\) (patrz: Krok 3.).
ALBO
• Gdy błędnie obliczysz wysokość trapezu, ale konsekwentnie do popełnionego błędu obliczysz pole trapezu.
2 pkt
• Gdy otrzymasz oczekiwany wynik.
Powiem szczerze, że zadanka w tym dziale są tutaj bardzo łatwiutkie, a jak się na maturze trafi „Kąt α jest ostry i spełniona jest równość sinα+cosα=7–√2. Oblicz wartość wyrażenia (sinα−cosα)2” to człowiekowi aż szczęka opada :(
Ależ wszystkie zadania na tej podstronie pochodzą właśnie z matur! Tak więc jeśli są one dla Ciebie łatwiutkie to mam świetną wiadomość – prawdopodobnie jesteś świetnie przygotowana do matury :)
Tego typu zadania o których mówisz są w dziale „Zależności między funkcjami trygonometrycznymi”.
https://szaloneliczby.pl/zaleznosci-miedzy-funkcjami-trygonometrycznymi-zadania-maturalne/
Trzymam kciuki za jak najlepsze wyniki!
Błąd w zadaniu 7. Wynik -4/5. Odpowiedź B
Zadanie jest zrobione poprawnie ;) Wzór to tgalfa=y/x, czyli właśnie -5/4.
Tg kąta ostrego w trójkącie prostokątnym nazywamy stosunek przyprostokątnej lezącej naprzeciw tego kąta do drugiej przyprostokątnej x/y
Definicję podałeś dobrą, ale po pierwsze nie znasz długości poszczególnych boków, a po drugie to w ogóle nie jest trójkąt prostokątny, bo kąt jest rozwarty ;)
W tym zadaniu wykorzystujemy wzory związane z przechodzeniem jednego z ramion przez dany punkt w układzie współrzędnych.
Powiem szczerze,nie rozumiem dlaczego w zad.9 h należy wyliczyć z tg alfa. Przecież można to zrobić z twierdzenia Pitagorasa i h=5,tylko że wtedy wynik ogólny wyjdzie 45.
Ale zaraz zaraz… Jak to obliczasz z Twierdzenia Pitagorasa, skoro w trójkącie prostokątnym znasz miarę tylko jednego boku? ;)
Widzę że te zadania są z matur, a dla mnie one są jakieś takie proste. Co prawda zacząłem się matematyki na poważnie uczyć od niedawna bo przedtem to raczej tylko się uczyłem żeby zdać ale teraz zrozumiałem że jest bardzo potrzebna.
Mam pytanie, bo w zadaniu 7 jak narysuje inny trapez, gdzie podzielę dolną podstawę na 6 i 2 i 2
to wychodzi mi wysokość 6, a nie 12 – więc to daje mi inny wynik
Ale ale… Ty rysujesz prawdopodobnie trapez równoramienny, a ma być prostokątny! :)
Mam pytanie do zadania 6. Jest tam uzyty wzór y/x a słyszałem ze można tego wzoru używać tylko w przypadku gdy jeden z boków kąta jest na osi X a w tamtym przypadku tegeo nie ma?
Dobrze słyszałeś – jedno ramię musi być na osi OX, a wierzchołek musi być w początku układu współrzędnych :) I dokładnie tak jest na tym rysunku (zwróć uwagę, że jest to kąt rozwarty!).
To nasza ulubiona strona do powtórek do matury. Pozdrawiamy 3 B (To znowu my XIX LO z Gdańska) :)
super zadanka, naprawdę łatwe
Dzien dobry.
(bardzo przepraszam, ze nie uzywam polskich znakow, mam zablokowany, palec i nie wygodnie naciskac prawy ALT)
Chcialbym dopytac na temat zadania numer 5. Czyzby, tam nie byl wynik B? Poniewaz jezeli mamy wyliczyc ta alfe ktora podana, to jest mniejsza przyprostokatna podzielona na wieksza.
Wieksza jest 5, mniejsza -4.
Btw, bardzo dziwnie jest ukazany kat alfa, ale to pewnie przez brak miejsca on zostal ukazany podobnie do rozwartego kata.
Tutaj nie chodzi o przyprostokątne :) To jest przykład kąta w układzie współrzędnych, gdzie jedno ramię trójkąta pokrywa się z osią OX, a wierzchołek jest w początku układu współrzędnych. W takiej sytuacji wystarczy skorzystać ze wzoru z tablic (który podałem w rozwiązaniu) i podstawić współrzędne punktu, przez które przechodzi drugie ramię ;)
Mam nadzieję, że tego typu zadanka będą na maturce, to wynik w okolicy 80-100% wykręcę :)
Fajne zadanka pozdrawiam z rodzinką
super zadanka :) polecam
hej, czemu w zad 1 odp to 1/pierwiastek z dwóch? Czy w takim przypadku nie musimy usunąć niewymierności?
Usuwanie niewymierności to dobry zwyczaj, ale nie jest to obowiązek ;) No i w tym zadaniu okazało się to niepotrzebne, bo z wynikiem musimy też się dostosować do proponowanych odpowiedzi ;)