Rozwiązanie
Krok 1. Zapisanie nierówności w postaci ogólnej.
Zanim przystąpimy do wykonywania obliczeń, musimy zapisać tę nierówność w postaci ogólnej. Musimy zatem wymnożyć nawiasy znajdujące się po lewej stronie i całość zapisu przekształcić w taki sposób, by po prawej stronie zostało samo zero.
$$2(x+1)(x-3)\lt x^2-9 \\
2(x^2-3x+x-3)\lt x^2-9 \\
2x^2-6x+2x-6\lt x^2-9 \\
2x^2-4x-6\lt x^2-9 \\
x^2-4x+3\lt0$$
Krok 2. Obliczenie miejsc zerowych wielomianu.
Współczynniki: \(a=1,\;b=-4,\;c=3\)
$$Δ=b^2-4ac=(-4)^2-4\cdot1\cdot3=16-12=4 \\
\sqrt{Δ}=\sqrt{4}=2$$
$$x_{1}=\frac{-b-\sqrt{Δ}}{2a}=\frac{-(-4)-2}{2\cdot1}=\frac{4-2}{2}=\frac{2}{2}=1 \\
x_{2}=\frac{-b+\sqrt{Δ}}{2a}=\frac{-(-4)+2}{2\cdot1}=\frac{4+2}{2}=\frac{6}{2}=3$$
Krok 3. Szkicowanie wykresu paraboli.
Zaznaczamy na osi wyliczone przed chwilą miejsca zerowe (z pustymi kropkami, bo w nierówności wystąpił znak \(\lt\)). Współczynnik \(a\) jest dodatni, więc parabola będzie mieć ramiona skierowane do góry, czyli całość będzie wyglądać następująco:
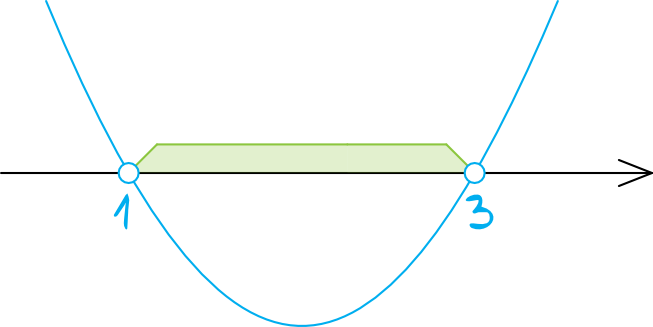
Krok 4. Odczytanie rozwiązania.
Szukamy argumentów dla których funkcja przyjmuje wartości mniejsze od zera, a więc rozwiązaniem nierówności będzie przedział:
$$x\in(1;3)$$