Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
W treści mamy sporo danych, więc spróbujmy je uporządkować na rysunku pomocniczym:
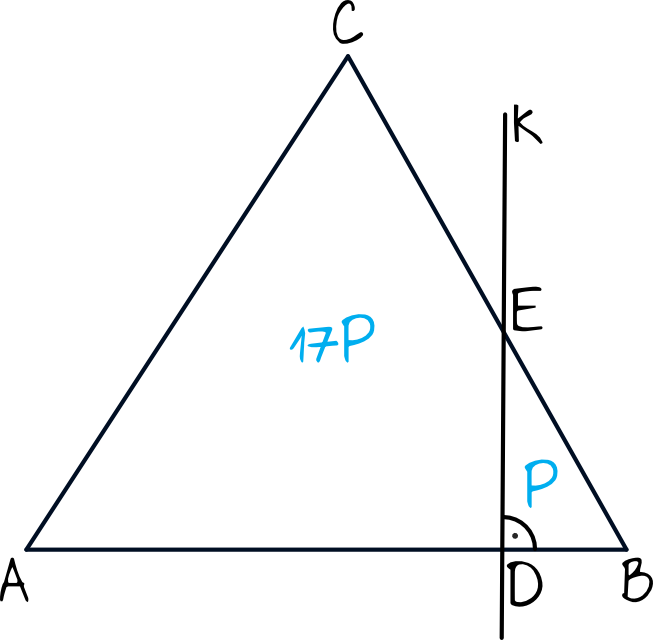
Z treści zadania wynika wprost, że nasz trójkąt jest równoramienny. W takim razie kluczem do sukcesu będą teraz dwie rzeczy - po pierwsze, musimy dostrzec, że cały trójkąt \(ABC\) ma pole powierzchni równe \(17P+P=18P\). Po drugie, jeżeli dorysujemy sobie wysokość z wierzchołka \(C\), to otrzymamy dwa trójkąty o polu \(9\) (bo wysokość w trójkącie równoramiennym dzieli nam trójkąty na dwie równe części).

Krok 2. Dostrzeżenie trójkątów podobnych i obliczenie skali podobieństwa.
Spójrzmy na trójkąty \(FBC\) oraz \(DBE\). Dzięki temu, że odcinki \(FC\) oraz \(DE\) są względem siebie równoległe (obydwa są prostopadłe do prostej \(AB\)) to możemy być pewni, że trójkąty \(FBC\) oraz \(DBE\) są trójkątami podobnymi (cecha kąt-kąt-kąt).
Spróbujmy zatem wyznaczyć skalę podobieństwa tych trójkątów. Widzimy, że pole trójkąta \(FBC\) wynosi \(9P\), a pole trójkąta \(DBE\) jest równe \(1P\). Z własności trójkątów podobnych wiemy, że gdy dany trójkąt jest podobny do drugiego w skali \(k\) to pole tego trójkąta będzie \(k^2\) razy większe. W naszym przypadku trójkąt \(FBC\) ma pole \(9\) razy większe od pola trójkąta \(DBE\), zatem:
$$k^2=9 \\
k=3 \quad\lor\quad k=-3$$
Ujemny wynik oczywiście odrzucamy, zatem zostaje nam \(k=3\).
Krok 3. Obliczenie długości odcinka \(CE\).
Wiemy już, że skala podobieństwa trójkątów \(FBC\) oraz \(DBE\) jest równa \(k=3\). To oznacza, że jeżeli bok \(BE\) ma długość \(x\), to odcinek \(BC\) będzie trzykrotnie większy, czyli jego długość będziemy mogli oznaczyć jako \(3x\).
Interesujący nas odcinek \(CE\) jest różnicą między długością odcinka \(BC\) oraz \(BE\), zatem:
$$|CE|=|BC|-|BE| \\
|CE|=3x-x \\
|CE|=2x$$
Krok 4. Obliczenie zależności \(\frac{|CE|}{|EB|}\).
Na sam koniec musimy obliczyć wartość \(\frac{|CE|}{|EB|}\). Znamy już długości obydwu odcinków, zatem możemy zapisać, że:
$$\frac{|CE|}{|EB|}=\frac{2x}{x}=2$$