Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Skoro wyjściowy prostokąt ma wymiary \(12\times6\) to możemy wprowadzić następujące oznaczenia:
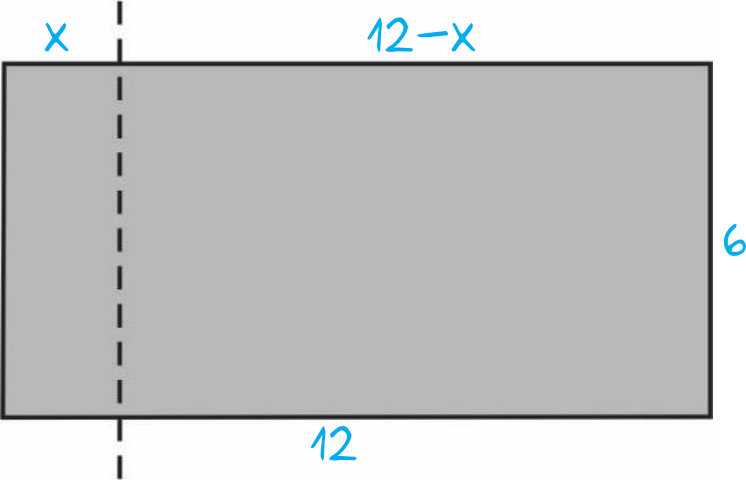
Krok 2. Obliczenie obwodów mniejszego i większego prostokąta.
Mniejszy prostokąt ma obwód równy:
$$Obw_{M}=2\cdot x+2\cdot6=2x+12$$
Większy prostokąt ma obwód równy:
$$Obw_{D}=2\cdot(12-x)+2\cdot6 \\
Obw_{D}=24-2x+12 \\
Obw_{D}=36-2x$$
Krok 3. Ułożenie i rozwiązanie równania.
Z treści zadania wiemy, że obwód dużego prostokąta jest dwukrotnie większy, zatem powstaje nam równanie:
$$Obw_{D}=2\cdot Obw_{M} \\
36-2x=2\cdot(2x+12) \\
36-2x=4x+24 \\
12=6x \\
x=2$$
Krok 4. Wyznaczenie wymiarów mniejszego prostokąta.
Patrząc się na rysunek pomocniczy widzimy, że nasz mniejszy prostokąt ma wymiary \(6\) i \(x\), czyli \(6\) i \(2\).