Prostokąt ABCD podzielono na 6 kwadratów: jeden duży, dwa średnie i trzy małe, jak na rysunku

Krok 1. Sporządzenie rysunku pomocniczego.
Oznaczmy sobie długość boku małego kwadratu jako \(x\). To będzie oznaczać, że duży kwadrat będzie mieć długość \(3x\), a średni kwadrat będzie mieć bok długości \(1,5x\):


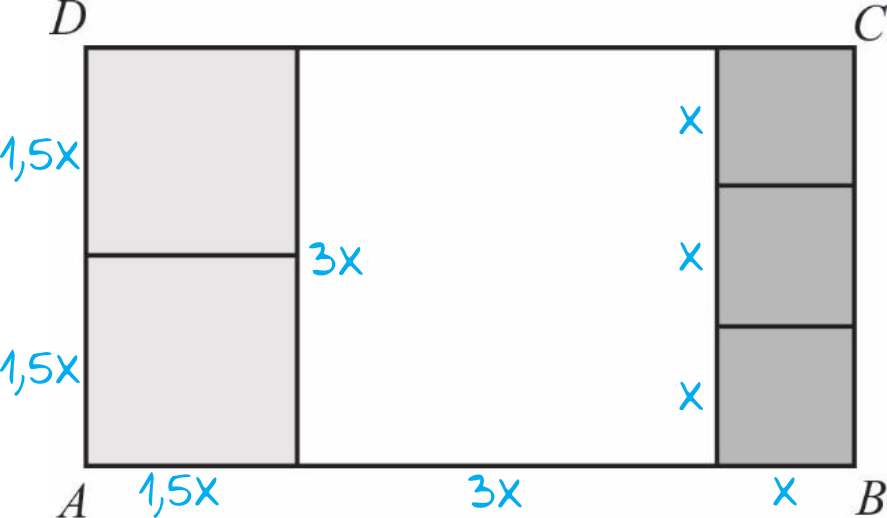
Krok 2. Obliczenie pola prostokąta \(ABCD\).
Zgodnie z rysunkiem możemy powiedzieć, że nasz prostokąt ma boki długości \(5,5x\) oraz \(3x\), zatem jego pole powierzchni będzie równe:
$$P=5,5x\cdot3x \\
P=16,5x^2$$

Krok 3. Obliczenie pola dużego kwadratu.
Duży kwadrat ma bok długości \(3x\), zatem jego pole powierzchni będzie równe:
$$P=3x\cdot3x \\
P=9x^2$$

Krok 4. Zakończenie dowodzenia.
Duży kwadrat ma pole równe \(9x^2\).
Połowa pola prostokąta \(ABCD\) wynosi \(16,5x^2:2=8,25x^2\).
To oznacza, że pole dużego kwadratu jest rzeczywiście większe niż połowa prostokąta \(ABCD\).