Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Deska sama w sobie ma dość nietypowy kształt, zatem jej powierzchni nie obliczymy ot tak podstawiając coś do wzoru na powierzchnię. Możemy jednak dostrzec, że dałoby się podzielić tę deskę na dwie różne figury, których pola będą możliwe do policzenia - kwadrat oraz połowa koła.
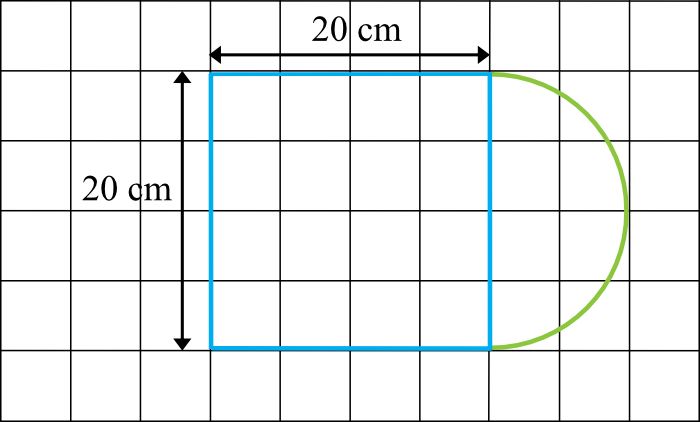
Krok 2. Obliczenie pola kwadratu.
Pierwszą figurą jest kwadrat o boku \(20cm\), zatem jego pole powierzchni będzie równe:
$$P=20cm\cdot20cm=400cm^2$$
Krok 3. Obliczenie pola połowy koła.
Drugą częścią naszej deski jest połowa koła. Jednak najpierw policzymy pole całego koła, a dopiero potem podzielimy sobie otrzymany wynik przez dwa. Wzór na pole koła jest następujący:
$$P=πr^2$$
Do obliczenia pola koła potrzebujemy znać długość promienia okręgu. Z rysunku widać, że każda kratka ma długość \(5cm\), zatem skoro promień okręgu ma długość dwóch kratek, to \(r=10cm\). To oznacza, że pole okręgu jest równe:
$$P=π\cdot(10cm)^2 \\
P=100πcm^2$$
Zgodnie z naszą analizą potrzebujemy połowy pola naszego koła. Zatem interesująca nas część będzie miała pole
$$P=100πcm^2:2=50πcm^2$$
Krok 4. Obliczenie pola powierzchni deski.
Pole deski jest sumą pola kwadratu oraz połówki koła, zatem:
$$P=400cm^2+50πcm^2$$