Na tej lekcji omówimy równanie okręgu. Pokażemy sobie jaką postać przyjmuje takie równanie, jakie informacje możemy z niego odczytać i przyjrzymy się przykładowym zadaniom z tego zagadnienia.
Okrąg o środku w punkcie \(S=(a,b)\) oraz promieniu \(r\) możemy opisać następującym równaniem:
$$(x-a)^2+(y-b)^2=r^2$$
Jeśli więc mamy okrąg, którego środek znajduje się w punkcie \(S=(3;-2)\), a promień ma długość \(r=5\), to taki okrąg moglibyśmy opisać równaniem:
$$(x-3)^2+(y-(-2))^2=5^2 \\
(x-3)^2+(y+2)^2=25$$
Pokażmy sobie teraz kilka przykładowych zadań, w których wykorzystamy równanie okręgu.
Rozwiązanie:
Bardzo ważne jest to, aby nie pogubić się w znakach. Równanie okręgu przyjmuje postać \((x-a)^2+(y-b)^2=r^2\) i zwróć uwagę, że wewnątrz nawiasów mamy tutaj minusy. W przypadku naszego równania \((x-5)^2+(y+3)^2=36\), wewnątrz drugiego nawiasu pojawił się plus, co musimy teraz uwzględnić podczas odczytywania współrzędnych środka okręgu. Aby lepiej to sobie zobrazować, nie stoi na przeszkodzie, by \(+3\) zamienić na \(-(-3)\), dzięki czemu nasze równanie przyjmie postać:
$$(x-5)^2+(y-(-3))^2=36$$
I teraz bardzo dobrze widać, że \(a=5\) oraz \(b=-3\), czyli środkiem okręgu będzie punkt \(S=(5,-3)\).
Musimy jeszcze obliczyć długość promienia. Zerkamy więc na prawą stronę równania. Liczba \(36\) musi odpowiadać wartości \(r^2\), czyli:
$$r^2=36 \\
r=6 \quad\lor\quad r=-6$$
Ujemną wartość odrzucamy, bo długość promienia musi być dodatnia. Stąd też zostaje nam \(r=6\).
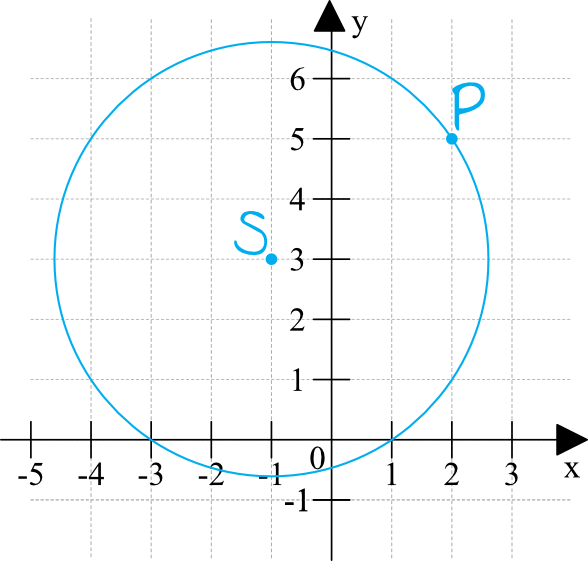
Rozwiązanie:
Do zapisania równania potrzebujemy współrzędnych środka okręgu i długości promienia. Współrzędne środka możemy wprost odczytać z rysunku i widzimy, że to będzie \(S=(-1;3)\). Brakuje nam jeszcze długości promienia. Możemy ją poznać na dwa sposoby.
I sposób – z wykorzystaniem wzoru na długość odcinka.
Odległość punktu \(S\) od punktu \(P\) to nic innego jak właśnie promień okręgu. Znamy współrzędne obydwu tych pól, więc możemy skorzystać ze wzoru na długość odcinka w układzie współrzędnych:
$$|SP|=\sqrt{(x_{P}-x_{S})^2+(y_{P}-y_{S})^2}$$
Podstawiając teraz współrzędne punktów \(S=(-1,3)\) oraz \(P=(2;5)\), otrzymamy:
$$|SP|=\sqrt{(2-(-1))^2+(5-3)^2} \\
|SP|=\sqrt{(2+1)^2+2^2} \\
|SP|=\sqrt{3^2+2^2} \\
|SP|=\sqrt{9+4} \\
|SP|=\sqrt{13}$$
To oznacza, że równanie okręgu przyjmie postać:
$$(x-(-1))^2+(y-3)^2=(\sqrt{13})^2 \\
(x+1)^2+(y-3)^2=13$$
II sposób – z wykorzystaniem twierdzenia Pitagorasa.
Na rysunku możemy naszkicować taki oto trójkąt prostokątny:
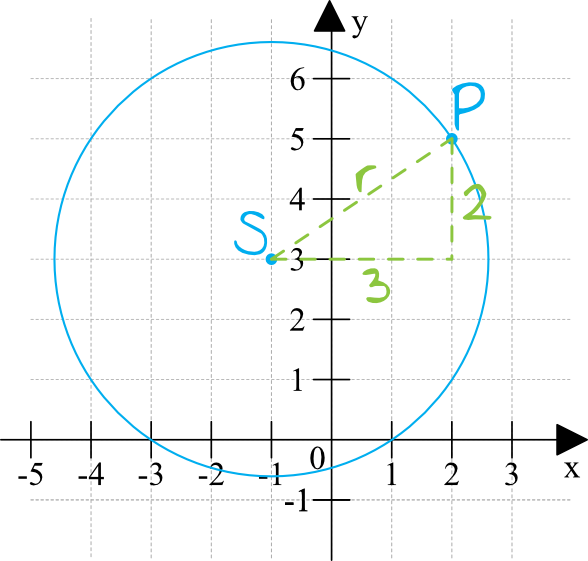
Długości przyprostokątnych odczytujemy po kratkach i widzimy, że będą to odpowiednio boki o długości \(3\) oraz \(2\). Długość promienia jest przeciwprostokątną tego trójkąta prostokątnego, zatem z pomocą przyjdzie nam twierdzenie Pitagorasa:
$$3^2+2^2=r^2 \\
9+4=r^2 \\
r^2=13$$
I tu mała podpowiedź – owszem, możemy obliczyć, że \(r=\sqrt{13}\), ale my do równania okręgu i tak podstawiamy \(r^2\). Jeśli więc celem zadania jest zapisanie równania okręgu, to możemy zostać przy równaniu \(r^2=13\). Zapisalibyśmy więc, że równanie okręgu to:
$$(x-(-1))^2+(y-3)^2=13 \\
(x+1)^2+(y-3)^2=13$$
Rozwiązanie:
Jeżeli jakiś punkt leży na okręgu, to współrzędne tego punktu powinny spełniać podane równanie. Mówiąc wprost – jeśli podstawiając współrzędne danego punktu do równania okręgu, to lewa i prawa strona równania powinny być sobie równe. Sprawdźmy zatem po kolei każdy z podanych punktów.
Zaczynamy od \(A=(3;2)\). Podstawiamy zatem \(x=3\) oraz \(y=2\) do równania \((x-5)^2+(y-3)^2=4\), otrzymując:
$$(3-5)^2+(2-3)^2=4 \\
(-2)^2+(-1)^2=4 \\
4+1=4 \\
5=4 \\
L\neq P$$
Otrzymany wynik oznacza, że punkt \(A\) nie leży na podanym okręgu.
Teraz analogicznie podstawiamy współrzędne punktu \(B=(5;1)\), czyli \(x=5\) oraz \(y=1\), zatem:
$$(5-5)^2+(1-3)^2=4 \\
0^2+(-2)^2=4 \\
0+4=4 \\
4=4 \\
L=P$$
Otrzymany wynik oznacza, że punkt \(B\) leży na naszym okręgu.
Zobacz także:
