Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Oznaczmy sobie wysokość trapezu jako \(h\). Aby powstały nam dwa trójkąty prostokątne równoramienne, to sytuacja z treści zadania musi wyglądać następująco:
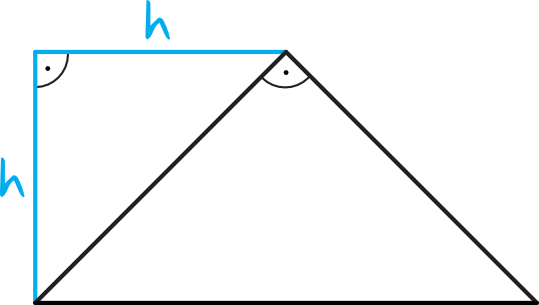
Krok 2. Ocena prawdziwości pierwszego zdania.
Z rysunku jasno wynika, że aby powstały nam dwa trójkąty prostokątne równoramienne, to faktycznie wysokość trapezu i krótsza podstawa muszą mieć tą samą długość. Zdanie jest więc prawdą.
Krok 3. Ocena prawdziwości drugiego zdania.
To zdanie będzie prawdą. Jak to udowodnić? Spójrzmy na trójkąt \(ACD\). Jest to trójkąt prostokątny o kątach \(45°, 45°, 90°\), zatem długość przekątnej trapezu będzie mieć długość \(h\sqrt{2}\). Ta sama długość musi być też długością ramienia \(BC\) (bo ma powstać nam trójkąt prostokątny równoramienny). W takim razie podstawa \(AB\) jest przeciwprostokątna trójkąta prostokątnego \(ABC\), który także jest trójkątem o kątach \(45°, 45°, 90°\). Jego długość będzie więc \(\sqrt{2}\) razy większa od długości przyprostokątnych, zatem:
$$|AB|=h\sqrt{2}\cdot\sqrt{2} \\
|AB|=2h$$
Na rysunku wyglądałoby to następująco:
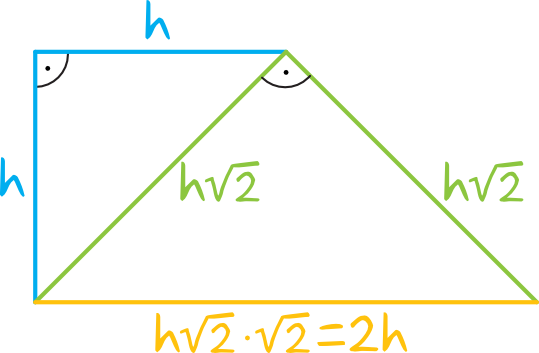
W ten oto sposób widzimy, że wysokość trapezu stanowi połowę dłuższej podstawy trapezu, stąd zdanie jest prawdą.