Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Zanim zaczniemy liczyć, to narysujmy sobie szkic tej całej sytuacji, zaznaczając przy okazji kluczowy kąt \(120°\):
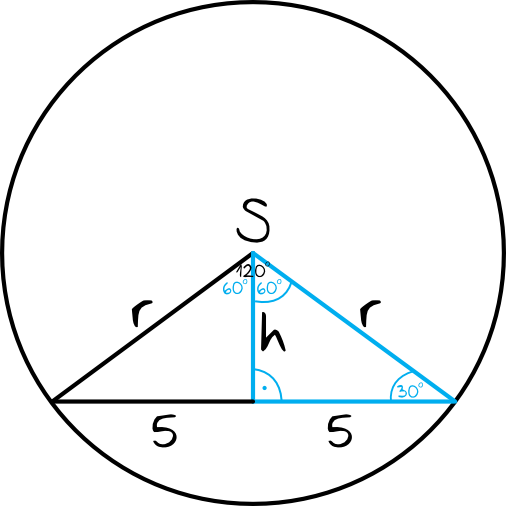
Zwróćmy uwagę na to, że powstał nam trójkąt prostokątny o kątach \(30°,60°,90°\). To właśnie on będzie kluczem do rozwiązania tego zadania. Musimy też zauważyć, że dolna przyprostokątna ma długość \(5\), bowiem w trójkątach równoramiennych wysokość dzieli nam podstawę na dwie równe części, a podstawa była równa \(10\).
Krok 2. Obliczenie promienia koła.
Korzystając z własności trójkątów o kątach \(30°,60°,90°\) wiemy, że jeżeli przyprostokątna leżąca przy kącie \(60°\) ma długość \(a\), to druga przyprostokątna ma długość \(a\sqrt{3}\), a przeciwprostokątna ma długość \(2a\).
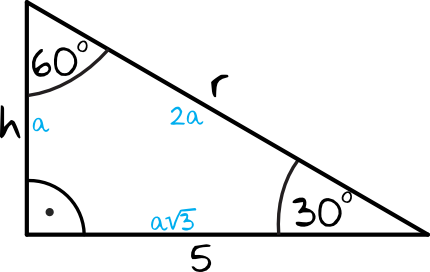
Zgodnie z naszymi oznaczeniami widzimy, że dolna przyprostokątna ma długość \(5\), zatem:
$$a\sqrt{3}=5 \\
a=\frac{5}{\sqrt{3}}$$
Nas interesuje długość przeciwprostokątnej, czyli długość \(2a\). W związku z tym:
$$r=2a=2\cdot\frac{5}{\sqrt{3}}=\frac{10}{\sqrt{3}}$$
Otrzymana odpowiedź jest już poprawna, ale powinniśmy jeszcze usunąć niewymierność z mianownika, a zrobimy to mnożąc licznik i mianownik przez \(\sqrt{3}\), zatem:
$$r=\frac{10\cdot\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}}=\frac{10\sqrt{3}}{3}$$