Rozwiązanie
Zadanie jest podchwytliwe, bo bardzo łatwo jest obliczyć niektóre klocki podwójnie (zwłaszcza te będące wierzchołkami bryły), dlatego warto sobie przeanalizować wszystko krok po kroku.
Krok 1. Sporządzenie rysunku pomocniczego.
Szkielet naszego prostopadłościanu będzie wyglądał mniej więcej w ten sposób:
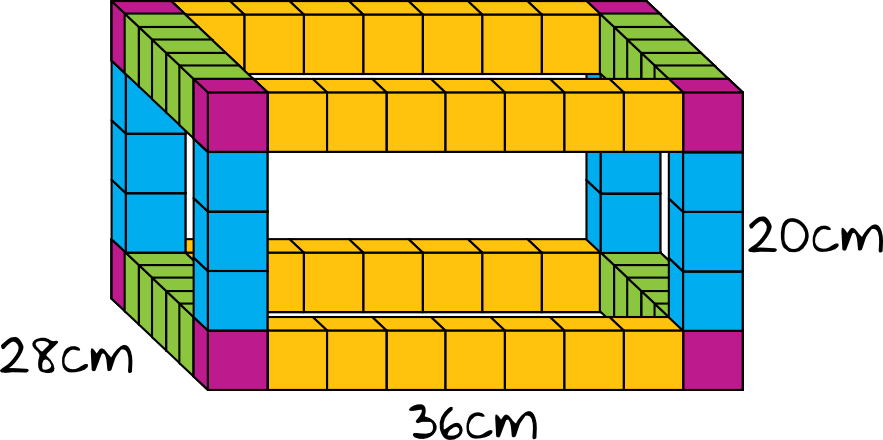
Krok 2. Obliczenie liczby pomarańczowych klocków.
Pomarańczowych klocków przy każdej krawędzi o długości \(36cm\) mamy dokładnie \(7\). Takich krawędzi mamy \(4\), zatem pomarańczowych klocków jest:
$$4\cdot7=28$$
Krok 3. Obliczenie liczby zielonych klocków.
Przy każdej krawędzi o długości \(28cm\) mieści się \(5\) klocków. Takich krawędzi mamy \(4\), zatem zielonych klocków jest:
$$4\cdot5=20$$
Krok 4. Obliczenie liczby niebieskich klocków.
Przy każdej krawędzi o długości \(20cm\) mieszczą się \(3\) klocki. Takich krawędzi mamy oczywiście \(4\), zatem niebieskich klocków jest:
$$4\cdot3=12$$
Krok 5. Obliczenie liczby fioletowych klocków.
Fioletowe klocki to te klocki znajdujące się w wierzchołkach graniastosłupa. Jest ich łącznie \(8\) sztuk.
Krok 6. Obliczenie łącznej liczby wszystkich klocków.
Wszystkich klocków mamy zatem:
$$28+20+12+8=68$$