Kąt środkowy i wpisany

Kąty środkowe i wpisane posiadają bardzo charakterystyczne własności, które są wykorzystywane w wielu zadaniach związanych z okręgami. Omówmy zatem te kąty i sprawdźmy, gdzie będziemy wykorzystywać zależności między nimi.

Co to jest kąt środkowy i kąt wpisany?
Zanim powiemy o własnościach kątów środkowych i wpisanych, pokażmy sobie może jak one wyglądają i czym się charakteryzują:

Bazując na rysunku możemy stwierdzić, że:
· kąt środkowy to kąt, którego wierzchołek znajduje się w środku okręgu,
· kąt wpisany to kąt, którego wierzchołek znajduje się na okręgu.

Łuk, na którym oparty jest kąt
Bardzo ważnym pojęciem jest łuk, na którym oparty jest dany kąt. To właśnie z łukami związane będą własności kątów środkowych i wpisanych. Łuki, na których opierają się nasze przykładowe kąty zostały zaznaczone na niebiesko:

Przy okazji warto dodać, że na jednym łuku może opierać się nieskończenie wiele kątów wpisanych i tylko jeden kąt środkowy:

Wydaje się to bardzo proste, ale są i takie kąty, które potrafią wprowadzić uczniów w zakłopotanie. Spójrzmy na taką sytuację:

Na powyższym rysunku kąt \(\alpha\) jest oparty na niebieskim łuku, natomiast kąt \(\beta\) oparty jest na łuku zielonym. Warto o tym pamiętać, ponieważ w bardziej złożonych zadaniach, złe określenie łuku jest źródłem wielu błędów.

Zależność między kątem środkowym i wpisanym
Okazuje się, że istnieje kluczowa zależność między kątem środkowym i wpisanym, które są oparte na tym samym łuku:

Twierdzenie o kącie środkowym i wpisanym opartych na tym samym łuku
Jeżeli kąt środkowy i wpisany są oparte na tym samym łuku, to miara kąta środkowego jest dwa razy większa od miary kąta wpisanego.

Dodatkowo kąty wpisane oparte na tym samym łuku mają jednakowe miary.

I od razu spójrzmy na przykładowe zadanie, w którym wykorzystamy omawiane twierdzenie:

Przykład 1. Oblicz miarę kąta \(\alpha\).

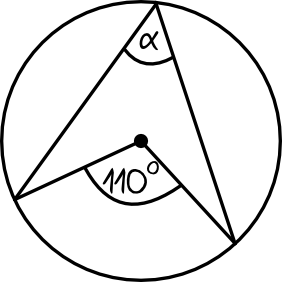
Rozwiązanie:
Widzimy wyraźnie, że kąt wpisany \(\alpha\) jest oparty na tym samym łuku co kąt środkowy \(110°\). To prowadzi nas do wniosku, że kąt \(\alpha\) będzie dwa razy mniejszy od kąta \(110°\), zatem:
$$\alpha=110°:2=55°$$

Przykład 2. Oblicz miarę kąta \(\alpha\) oraz \(\beta\).

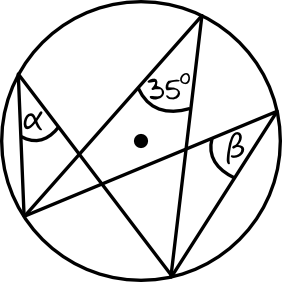
Rozwiązanie:
Tym razem mamy kąty wpisane, które oparte są na tym samym łuku. To oznacza, że miara każdego z tych kątów będzie jednakowa, co prowadzi nas do wniosku, że \(\alpha=35°\) oraz \(\beta=35°\).

To były bardzo proste przykłady, które pokazują ideę zadań z kątami środkowymi i wpisanymi. Pokażmy sobie teraz zadanie, które cały czas będzie bazować na tych samych własnościach, ale które będzie nieco trudniejsze.

Przykład 3. Oblicz miarę kąta \(\alpha\).

Rozwiązanie:
Na początku ustalmy, czy kąt środkowy o mierze \(200°\) jest oparty na tym samym łuku co poszukiwany przez nas kąt \(\alpha\). Jeśli tak, to zadanie będzie proste, bo w takim przypadku \(\alpha\) byłaby kątem dwa razy mniejszym. Niestety, te kąty nie są oparte na tych samych łukach (kąt o mierze \(200°\) jest oparty na zupełnie przeciwnym łuku niż kąt \(\alpha\)). To jest właśnie jedna z kluczowych pułapek w tego typu zadaniach.

Jak więc możemy podejść do tego zadania? Tu powinniśmy zauważyć, że kątem opartym na tym samym łuku co \(\alpha\) będzie ten oto kąt \(\beta\):

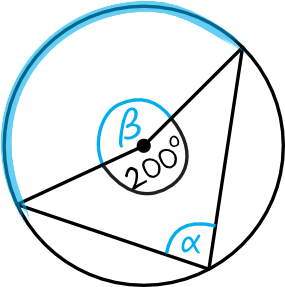
Miara tego kąta \(\beta\) będzie równa tyle co kąt pełny \(360°\) odjąć właśnie nasz kąt o mierze \(200°\), zatem:
$$\beta=360°-200°=160°$$

I dopiero teraz możemy skorzystać z własności kątów opartych na tym samym łuku. Miara kąta wpisanego \(\alpha\) musi być dwa razy mniejsza od kąta środkowego \(\beta\), zatem:
$$\alpha=160°:2=80°$$

Przy okazji tego tematu warto wspomnieć o dość specyficznej sytuacji, gdy kąt wpisany oparty jest na średnicy okręgu:

Kąt wpisany oparty na średnicy okręgu jest kątem prostym.

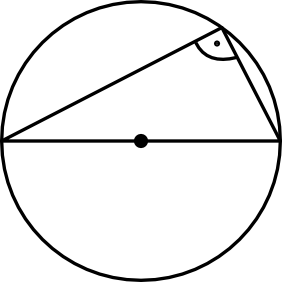
Powyższą zależność możemy kojarzyć z tematu okręgów opisanych na trójkątach. Mówiąc bardzo obrazowo, jeżeli mamy sytuację, w której bok trójkąta pokrywa się ze średnicą okręgu, to możemy być pewni, że jest to trójkąt prostokątny, a średnica okręgu jest wtedy jednocześnie przeciwprostokątną trójkąta. Ta własność wynika właśnie wprost z kątów wpisanych i środkowych. W omawianej powyżej sytuacji kąt środkowy ma miarę \(180°\) i dlatego też kąt wpisany ma miarę \(180°:2=90°\).

Przykład 4. Wyznacz wszystkie miary trójkąta \(ABC\).

Rozwiązanie:
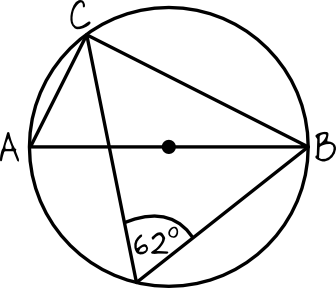
Powinniśmy zauważyć, że omawiany trójkąt jest prostokątny, ponieważ jeden z jego boków opiera się na średnicy okręgu. To oznacza, że \(|\sphericalangle ACB|=90°\). Miarę drugiego kąta wyznaczymy korzystając z własności kątów wpisanych. Kąt \(CAB\) jest kątem wpisanym, który jest oparty na tym samym łuku co kąt o znanej mierze \(62°\). Skoro tak, to \(|\sphericalangle CAB|=62°\). Znamy więc już miary dwóch kątów w tym trójkącie, a skoro suma kątów w każdym trójkącie jest równa \(180°\), to:
$$|\sphericalangle ABC|=180°-90°-62°=28°$$

To oznacza, że nasz trójkąt \(ABC\) ma kąty o mierze \(28°, 62°, 90°\).

Zobacz także: