Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Dobry rysunek jest tutaj kluczem do rozwiązania zadania. Narysujmy więc wskazany okręg, tak aby był on styczny do osi igreków i prostej o równaniu \(y=2\):
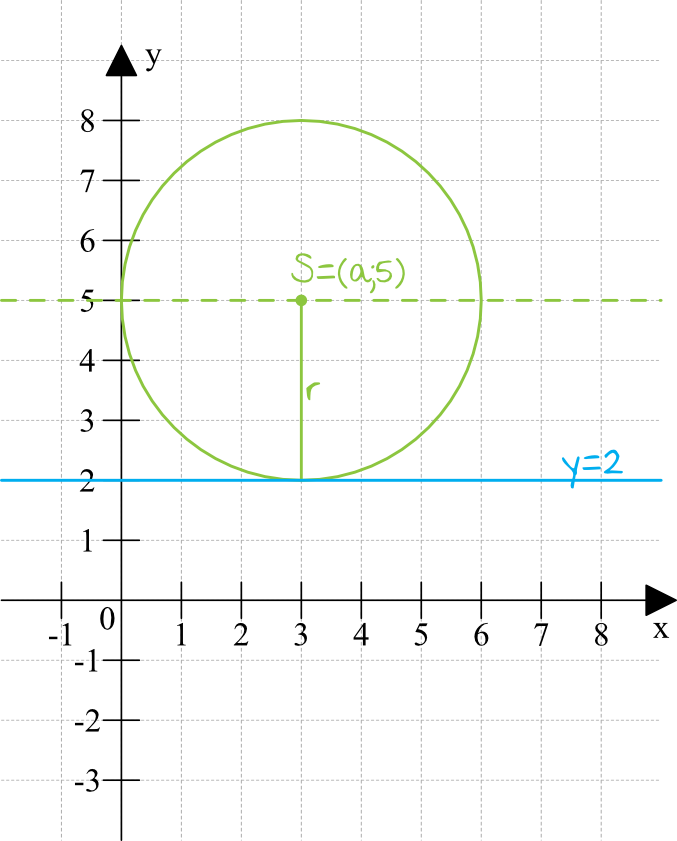
Krok 2. Obliczenie długości promienia.
Z rysunku widać wyraźnie, że promień naszego okręgu to będzie odcinek od środka okręgu do prostej \(y=2\). Odcinek ten ma długość trzech jednostek (bo \(5-2=3\)), zatem \(r=3\).