Rozwiązanie
Krok 1. Obliczenie odległości \(P\) od punktu \(B\).
Zaczniemy od prostszej części tego zadania, czyli od drugiego pytania. Musimy sobie odpowiedzieć na pytanie jaka jest odległość punktu \(P\) od \(B\), czyli tak naprawdę jaka jest długość odcinka \(PB\). Z treści zadania wiemy, że długość tego odcinka jest równa \(\frac{1}{5}\) długości odcinka \(BC\), zatem:
$$\frac{1}{5}\cdot65m=13m$$
To oznacza, że \(PB=13m\).
Krok 2. Obliczenie odległości punktu \(P\) od prostej \(AB\).
Odległość punktu od prostej mierzymy zawsze po najkrótszej linii (czyli będzie to zawsze się odbywać pod kątem prostym). Poszukiwana odległość jest już zaznaczona na rysunku, więc można powiedzieć że tym razem musimy obliczyć długość odcinka \(FP\). Jak to zrobić? Zróbmy sobie prosty rysunek szkicowy:
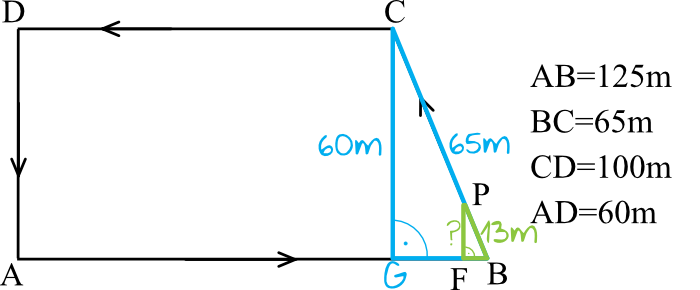
Na powyższym rysunku dorysowaliśmy sobie odcinek \(CG\), który ma dokładnie tą samą długość co odcinek \(AD\) i który pada pod kątem prostym na prostą \(AB\). Użyjemy tego odcinka do obliczenia długości odcinka \(FP\). W tym celu skorzystamy z własności trójkątów podobnych \(CGB\) oraz \(PFB\). Skąd wiadomo, że te dwa trójkąty są podobne? Mają one wspólny kąt \(GBC\), mają też jeden kąt prosty, więc skoro miary dwóch kątów są jednakowe w tych trójkątach to i ten trzeci kąt ma jednakową miarę. W ten sposób udowodniliśmy podobieństwo trójkątów zgodnie z cechą kąt-kąt-kąt.
Skoro udowodniliśmy podobieństwo trójkątów to możemy zapisać że:
$$\frac{CB}{CG}=\frac{PB}{PF} \\
65\cdot PF=60\cdot13
65\cdot PF=780
PF=12[m]$$