Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Aby rozpocząć rozwiązywanie zadania spróbujmy sobie naszkicować nasz trapez, tak aby dostrzec wszelkie zależności z których potem będziemy mogli skorzystać:
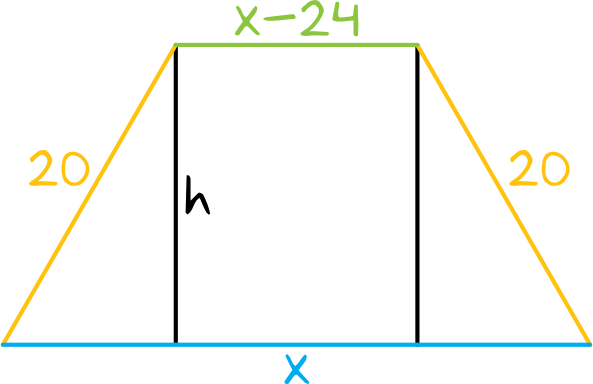
Krok 2. Obliczenie długości podstawy dolnej i górnej.
Skoro obwód naszego trapezu jest równy \(72cm\), a ramiona mają długość po \(20cm\) każde, to na obydwie podstawy zostaje nam:
$$72cm-20cm-20cm=32cm$$
Zapiszmy teraz to co wiemy o naszych podstawach w formie wyrażeń algebraicznych:
\(x\) - długość dłuższej podstawy (dolnej)
\(x-24\) - długość krótszej podstawy (górnej)
Skoro suma tych dwóch podstaw ma mieć długość \(32cm\), to prawdziwym będzie równanie:
$$x+(x-24)=32 \\
2x-24=32 \\
2x=56 \\
x=28[cm]$$
To oznacza, że dłuższa podstawa ma \(28cm\), a krótsza ma \(28cm-24cm=4cm\).
Krok 3. Obliczenie długości odcinka \(AE\).
Z własności trapezów równoramiennych wiemy, że \(|AE|=|FB|\). Możemy też wywnioskować, że suma tych dwóch odcinków jest równa dokładnie \(24cm\), czyli tyle ile wynosi różnica między podstawami trapezu. Skoro tak, to odcinek \(AE\) ma długość równą połowie tej różnicy, czyli \(24cm:2=12cm\).
Krok 4. Obliczenie wysokości trapezu.
Skorzystamy tutaj z trójkąta \(AED\) i Twierdzenia Pitagorasa. Szukamy wysokości \(DE\), a znamy już miary \(AE\) oraz \(AD\), zatem:
$$12^2+h^2=20^2 \\
144+h^2=400 \\
h^2=256 \\
h=16[cm]$$
Krok 5. Obliczenie pola trapezu.
Znamy już wszystkie potrzebne miary, zatem możemy przystąpić do obliczenia pola trapezu:
$$P=\frac{1}{2}(a+b)\cdot h \\
P=\frac{1}{2}(28+4)\cdot16 \\
P=\frac{1}{2}\cdot32\cdot16 \\
P=16\cdot16 \\
P=256[cm^2]$$