Rozwiązanie
Krok 1. Ocena prawdziwości pierwszego zdania.
Jeżeli kąty ostre rombu mają miarę \(60°\), to kąty rozwarte w tym rombie będą mieć \(120°\), bo kąty przy jednym boku rombu mają łącznie \(180°\).
Krótsza przekątna rombu będzie dwusieczną naszego kąta rozwartego (patrz poniższy rysunek), zatem faktycznie powstaną nam trójkąty o kątach \(60°, 60°, 60°\), czyli powstaną nam trójkąty równoboczne. Zdanie jest więc prawdą.
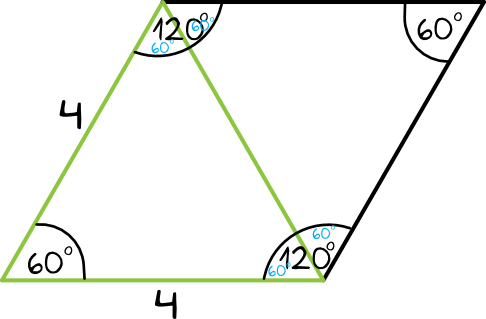
Krok 2. Ocena prawdziwości drugiego zdania.
Pole rombu będzie równe polu powierzchni dwóch trójkątów równobocznych o boku \(a=4\). Pole pojedynczego takiego trójkąta możemy obliczyć ze wzoru:
$$P=\frac{a^2\sqrt{3}}{4}$$
Skoro pole rombu składa się z dwóch takich trójkątów, to otrzymamy:
$$P_{r}=2\cdot\frac{a^2\sqrt{3}}{4} \\
P_{r}=\frac{a^2\sqrt{3}}{2} \\
P_{r}=\frac{16\sqrt{3}}{2} \\
P_{r}=8\sqrt{3}$$
Zdanie jest więc prawdą.