Dane są wierzchołki trójkąta ABC: A=(2,2), B=(9,5) i C=(3,9). Z wierzchołka C

Dane są wierzchołki trójkąta \(ABC\): \(A=(2,2)\), \(B=(9,5)\) i \(C=(3,9)\). Z wierzchołka \(C\) poprowadzono wysokość tego trójkąta, która przecina bok \(AB\) w punkcie \(D\). Wyznacz równanie prostej przechodzącej przez punkt \(D\) i równoległej do boku \(BC\).

Spróbujmy zobrazować tą sytuację, zaznaczając poszczególne punkty w układzie współrzędnych.

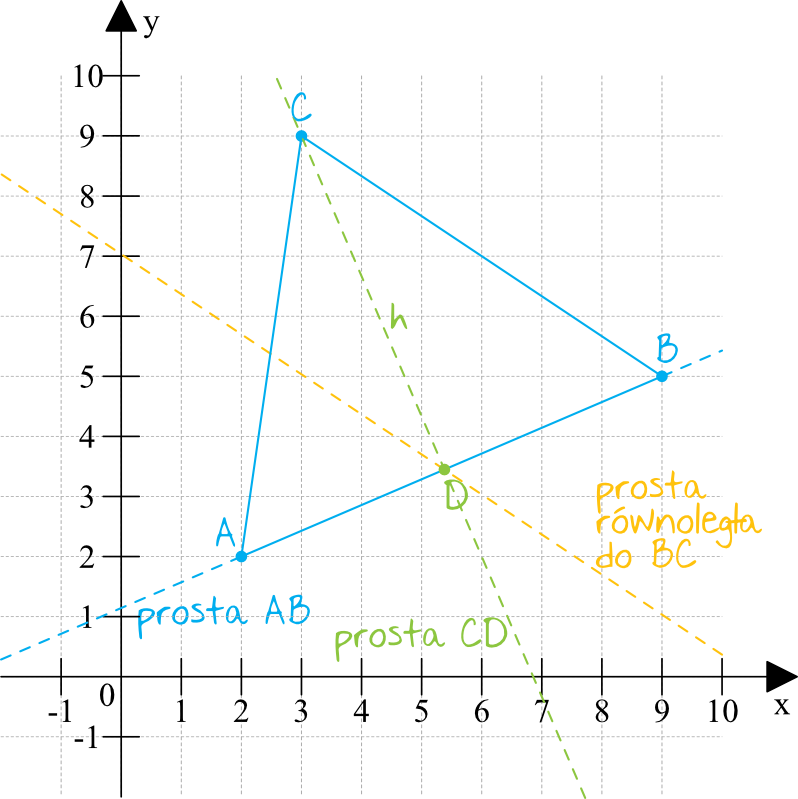
Ustalmy teraz co musimy obliczyć. Chcemy przede wszystkim wyznaczyć współrzędne punktu \(D\). Jednak żeby to zrobić, to musimy najpierw wyznaczyć równanie prostej przechodzącej przez punkty \(AB\), a następnie musimy znaleźć prostą prostopadłą do tej prostej, która przechodzi przez punkt \(C\). Punkt \(D\) będzie miejscem przecięcia się tych dwóch prostych. Na sam koniec musimy jeszcze wyznaczyć prostą równoległą do boku \(BC\), która przejdzie przez punkt \(D\). No to po kolei:

Możemy albo skorzystać ze wzoru na prostą przechodzącą przez punkty \(AB\), albo ułożyć i rozwiązać układ równań w którym do wzoru ogólnego \(y=ax+b\) podstawimy raz współrzędne punktu \(A\), a drugi raz współrzędne punktu \(B\).
\begin{cases}
2=2a+b \\
5=9a+b
\end{cases}

Odejmując to równanie stronami otrzymamy:
$$-3=-7a \\
a=\frac{3}{7}$$

Znając współczynnik \(a\) możemy z dowolnego równania wyznaczyć także współczynnik \(b\):
$$2=2\cdot\frac{3}{7}+b \\
2=\frac{6}{7}+b \\
b=\frac{8}{7}$$

To oznacza, że prosta \(AB\) jest opisana równaniem \(y=\frac{3}{7}x+\frac{8}{7}\).

Skoro prosta \(CD\) jest ma być prostopadła do prostej \(AB\), a to znaczy że iloczyn ich współczynników kierunkowych musi być równy \(-1\). Skoro prosta \(AB\) ma współczynnik \(a=\frac{3}{7}\), to prosta \(CD\) ma współczynnik \(a\) równy:
$$a\cdot\frac{3}{7}=-1 \\
a=-\frac{7}{3}$$

Wiemy już, że nasza prosta musi się wyrażać wzorem \(y=-\frac{7}{3}x+b\). Brakuje nam jeszcze współczynnika \(b\), ale skoro prosta przechodzi przez punkt \(C\) o znanych nam współrzędnych, to podstawiając te współrzędne do wzoru bez problemu obliczymy brakujący współczynnik:
$$y=-\frac{7}{3}x+b \\
9=-\frac{7}{3}\cdot3+b \\
9=-7+b \\
b=16$$

To oznacza, że prosta \(CD\) jest opisana równaniem \(y=-\frac{7}{3}x+16\).

Zgodnie z geometryczną interpretacją układu równań, rozwiązanie układu równań dwóch prostych da wynik będący miejscem przecięcia się tych prostych, czyli w naszym przypadku otrzymamy współrzędne punktu \(D\).
\begin{cases}
y=\frac{3}{7}x+\frac{8}{7} \\
y=-\frac{7}{3}x+16
\end{cases}

Podstawiając wartość \(y\) z pierwszej funkcji do drugiej otrzymamy:
$$\frac{3}{7}x+\frac{8}{7}=-\frac{7}{3}x+16 \quad\bigg/\cdot21 \\
9x+24=-49x+336 \\
58x=312 \\
x=\frac{312}{58}=\frac{156}{29}$$

Podstawiajac wartość \(x=\frac{156}{29}\) do dowolnego z równań zapisanego wcześniej układu (do drugiego będzie chyba łatwiej, bo tam mamy tylko jeden ułamek) wyznaczymy współrzędną \(y\):
$$y=-\frac{7}{3}\cdot\frac{156}{29}+16 \\
y=-\frac{1092}{87}+16 \\
y=-\frac{364}{29}+16 \\
y=-\frac{364}{29}+\frac{464}{29} \\
y=\frac{100}{29}$$

Zatem \(D=\left(\frac{156}{29};\frac{100}{29}\right)\).

Zanim wyznaczymy prostą równoległą do prostej \(BC\), to musimy poznać równanie tej prostej \(BC\). Wyznaczymy je dokładnie w ten sam sposób co równanie prostej \(AB\) z kroku drugiego.
\begin{cases}
5=9a+b \\
9=3a+b
\end{cases}

Odejmujemy równanie stronami i otrzymujemy:
$$-4=6a \\
a=-\frac{4}{6}=-\frac{2}{3}$$

I w zasadzie tyle nam wystarczy, nie potrzebujemy już obliczać współczynnika \(b\). Wystarczy nam sam współczynnik \(a\) bo to właśnie on jest potrzebny do wyznaczenia prostej równoległej.

I to jest już ostatnia rzecz którą musimy zrobić – czyli wyznaczyć wzór prostej równoległej do \(BC\), która przechodzi przez punkt \(D\). Aby dwie proste były względem siebie równoległe to muszą mieć jednakowy współczynnik \(a\). My w poprzednim punkcie ten współczynnik sobie wyznaczyliśmy, zatem wiemy już, że ta poszukiwana prosta równoległa będzie opisana wzorem:
$$y=-\frac{2}{3}x+b$$

Brakuje nam współczynnika \(b\), ale bez problemu go wyznaczymy podstawiając do tej prostej współrzędne punktu \(D\), które wyliczyliśmy w czwartym kroku, zatem:
$$\frac{100}{29}=-\frac{2}{3}\cdot\frac{156}{29}+b \\
\frac{100}{29}=-\frac{312}{87}+b \\
\frac{100}{29}=-\frac{104}{29}+b \\
b=\frac{204}{29}$$

Szukana prosta równoległa ma więc równanie: \(y=-\frac{2}{3}x+\frac{204}{29}\).

\(y=-\frac{2}{3}x+\frac{204}{29}\)