Cztery jednakowe prostopadłościenne klocki, każdy o wymiarach 2cm x 1cm x 1cm

Cztery jednakowe prostopadłościenne klocki, każdy o wymiarach $2cm\times1cm\times1cm$, ułożono tak, jak przedstawiono na rysunku.

Następnie do tej budowli dołożono sześcienne klocki o krawędzi długości $1$ cm tak, a by powstał prostopadłościan najmniejszy z możliwych. Uzupełnij zdania.

Liczba sześciennych klocków o krawędzi długości $1$ cm, które należy dołożyć do budowli, jest równa ____.

Najmniejszy z możliwych prostopadłościanów, który w ten sposób otrzymano, ma wymiary _ $cm \times$ _ $cm \times$ _ $cm$.

Rozwiązanie

Krok 1. Ustalenie wymiarów prostopadłościanu.
Na początku spróbujmy ustalić jakie to wymiary będzie mieć nasz nowo powstały prostopadłościan. Najlepiej będzie to widać na rysunku pomocniczym:
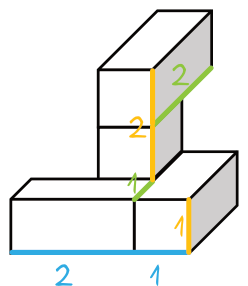
egzamin ósmoklasisty

Po zsumowaniu odpowiednich długości widzimy wyraźnie, że nasz prostopadłościan będzie mieć wymiary $3cm\times3cm\times3cm$.

Krok 2. Ustalenie ile klocków sześciennych trzeba dołożyć.
Nasz prostopadłościan będzie mieć wymiary $3cm\times3cm\times3cm$, czyli jego objętość będzie równa:
$$V=3cm\cdot3cm\cdot3cm \\
V=27cm^3$$

W tym prostopadłościanie znajdują się już cztery klocki o wymiarach $2cm\times1cm\times1cm$, czyli ich łączna objętość jest równa:
$$V=4\cdot2cm\cdot1cm\cdot1cm \\
V=4\cdot2cm^3 \\
V=8cm^3$$

To oznacza, że do zapełnienia kostkami sześciennymi zostaje nam przestrzeń równa $27cm^3-8cm^3=19cm^3$.

Sześcienne kostki, które mamy dołożyć, mają długość krawędzi równą $1cm$. W związku z tym objętość każdego takiego klocka jest równa:
$$V=1cm\cdot1cm\cdot1cm \\
V=1cm^3$$

W związku z tym liczba klocków sześciennych, które musimy dołożyć będzie równa:
$$19cm^3:1cm^3=19$$

Odpowiedź

$19$ klocków oraz $3cm\times3cm\times3cm$

Podaj swój nick lub imię*

E-mail

8 komentarzy

Inline Feedbacks

View all comments

kaizo

A nie powinien być prostopadłościan a nie sześcian?

Odpowiedz

SzaloneLiczby

Autor

Reply to kaizo

Dokładane kostki są sześcianami o krawędzi 1cm :)

Anix

Skąd się wzięło to ostatnie 3 w 3x3x3?

Reply to Anix

To są wymiary najmniejszego z możliwych prostopadłościanów (patrz rysunek) :)

Mariusz

Nie rozumiem dlaczego tworzymy sześcian jak w pytaniu proszą nas o utworzenie prostopadłościanu.

Reply to Mariusz

Sześcian jest także prostopadłościanem :) No i tak się złożyło (przypadkowo), że to akurat sześcian będzie tym najmniejszym z możliwych prostopadłościanów.

grzyb

Nie rozumiem dlaczego na rysunku pomocniczym jest napisane że 2cm, dlaczego akurat 2?

Reply to grzyb

Krawędź sześcianu ma długość 1, więc tam gdzie są dwie krawędzie obok siebie, tam mamy 2 :)