Rozwiązanie
Krok 1. Analiza rysunku.
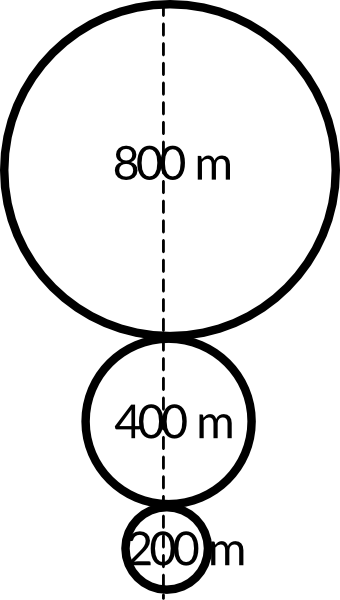
Zauważmy, że ślad na śniegu składa się tak naprawdę z trzech części, z których każda jest połową obwodu jakiegoś okręgu. Pierwszy łuk jest połową okręgu o średnicy \(800m\), drugi łuk jest połową okręgu o średnicy \(400m\), a trzeci łuk jest połową okręgu o średnicy \(200m\).
Krok 2. Obliczenie połówek obwodu każdego z trzech okręgów.
Wiemy już, że jak poznamy długości trzech obwodów okręgów (a w zasadzie ich połówek) to w prosty sposób dojdziemy do rozwiązania zadania. Wzór na obwód okręgu jest następujący:
$$Obw=2πr$$
Skoro potrzebujemy długości połowy okręgu, to możemy nawet zapisać, że wzór na pojedynczy łuk to:
$$Łuk=\frac{1}{2}\cdot2πr=πr$$
I tu uwaga, bo ukryła się tutaj największa pułapka. We wzorze musimy skorzystać z promienia okręgu, natomiast my na rysunku mamy zaznaczone średnice! Promień jest dwa razy mniejszy od średnicy, zatem:
I łuk: \(r=400m\)
II łuk: \(r=200m\)
III łuk: \(r=100m\)
Teraz możemy przystąpić do obliczeń:
I łuk: \(πr=400π\;m\)
II łuk: \(πr=200π\;m\)
III łuk: \(πr=100π\;m\)
Krok 3. Obliczenie długości trasy.
Suma trzech łuków jest poszukiwaną przez nas długością trasy, zatem:
$$400π\;m+200π\;m+100π\;m=700π\;m$$