Rozwiązanie
Krok 1. Wyznaczenie miejsc zerowych funkcji.
Wyznaczenie miejsc zerowych funkcji pomoże nam wyznaczyć współrzędną \(p\) wierzchołka paraboli \(W=(p;q)\), przez którą będzie przechodzić poszukiwana oś symetrii.
Funkcja kwadratowa jest zapisana w postaci iloczynowej, co bardzo ułatwia nam obliczenia. Szukamy miejsc zerowych, czyli musimy tak naprawdę rozwiązać równanie kwadratowe:
$$\frac{1}{7}(x-5)(x+9)=0$$
Aby wartość równania była równa \(0\), to któraś z wartości znajdujących się w nawiasach musi być równa \(0\), zatem:
$$x-5=0 \quad\lor\quad x+9=0 \\
x=5 \quad\lor\quad x=-9$$
Wyszło nam więc, że nasza funkcja ma dwa miejsca zerowe: \(x=-9\) oraz \(x=5\).
Krok 2. Wyznaczenie współrzędnej \(p\) wierzchołka paraboli.
Współrzędną wierzchołka \(p\) możemy wyliczyć na różne sposoby. Teoretycznie moglibyśmy nawet przekształcić wzór funkcji do postaci ogólnej i wtedy moglibyśmy skorzystać ze wzoru \(p=\frac{-b}{2a}\). My skorzystamy tutaj z szybszej metody, bowiem współrzędna \(p\) wierzchołka paraboli jest zawsze dokładnie pośrodku między miejscami zerowymi. Możemy zatem zapisać, że:
$$p=\frac{-9+5}{2} \\
p=\frac{-4}{2} \\
p=-2$$
Krok 3. Wyznaczenie równania osi symetrii.
Oś symetrii to prosta, która przechodzi przechodzi przez współrzędną \(p\) i która wygląda w ten sposób:
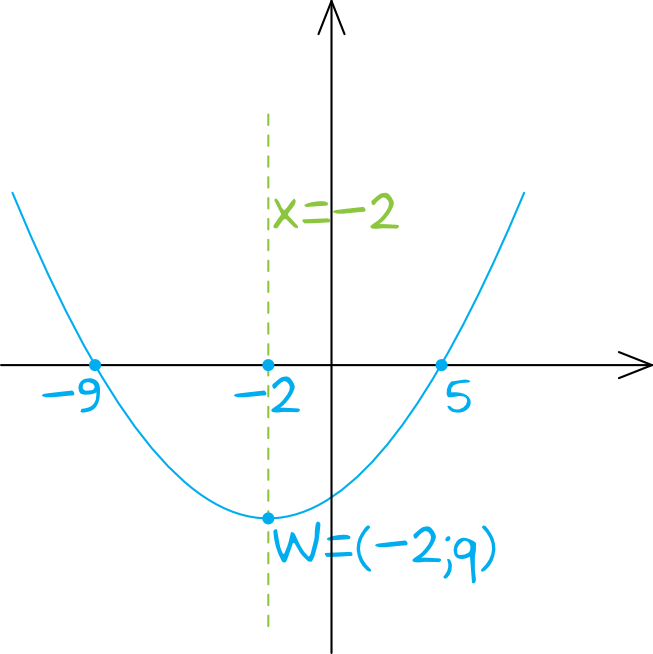
To oznacza, że osią symetrii będzie prosta o równaniu \(x=-2\).