Przekrojem osiowym stożka jest trójkąt równoboczny o boku długości \(6\). Objętość tego stożka jest równa:
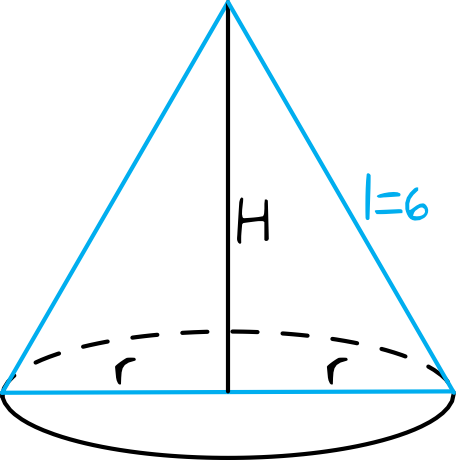
Spójrzmy na rysunek szkicowy. Do obliczenia objętości będziemy potrzebować długości promienia oraz wysokości bryły. Skoro przekrój jest trójkątem równobocznym, to na pewno wysokość dzieli podstawę na dwie równe części, a to z kolei oznacza że \(r=6:2=3\).
Wysokość \(h\) także nie stanowi problemu, bo mamy w tablicach wzór na wysokość trójkąta równobocznego:
$$h=\frac{a\sqrt{3}}{2}=\frac{6\sqrt{3}}{2}=3\sqrt{3}$$
Gdybyśmy nie pamiętali o tym wzorze, to wysokość można byłoby obliczyć z Twierdzenia Pitagorasa.
Znamy długość promienia, znamy wysokość, więc podstawiając dane do wzoru obliczymy objętość stożka:
$$V=\frac{1}{3}πr^2h \\
V=\frac{1}{3}π\cdot3^2\cdot3\sqrt{3} \\
V=\frac{1}{3}π\cdot9\cdot3\sqrt{3} \\
V=3\cdot3\sqrt{3}π \\
V=9\sqrt{3}π$$
B. \(9π\sqrt{3}\)

