Rozwiązanie
Krok 1. Ocena prawdziwości pierwszego zdania.
Obwód pierwszej figury będzie równy:
$$Obw_{I}=b+b+b+a+a+a+a+b+b+b \\
Obw_{I}=4a+6b$$
Obwód drugiej figury będzie równy:
$$Obw_{II}=a+b+b+b+a+b+b+b \\
Obw_{II}=2a+6b$$
To oznacza, że pierwsze zdanie jest fałszem, bo obwód I figury jest większy o \(2a\), a nie o \(2b\).
Krok 2. Ocena prawdziwości drugiego zdania.
Powinniśmy dostrzec, że każdy element układanki ma pole powierzchni równe \(3a^2\).
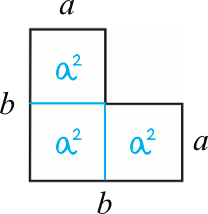
Druga figura składa się z czterech elementów, zatem jej pole będzie równe:
$$P=4\cdot3a^2 \\
P=12a^2$$
Zdanie jest więc prawdą.