W temacie wielokątów podobnych mówiliśmy sobie, że poszczególne figury uznajemy za podobne wtedy, gdy mają one jednakowe miary kątów i gdy poszczególne boki jednej figury są tyle samo razy większe lub mniejsze co drugiej figury. Te reguły dotyczą wszystkich wielokątów, także trójkątów. Okazuje się jednak, że w przypadku trójkątów, znając pewne charakterystyczne cechy, możemy znacznie szybciej określić czy dane figury są podobne i właśnie tym zajmiemy się w poniższym temacie.
Jeśli chcesz sobie przypomnieć podstawową wiedzę o wielokątach podobnych, to warto zajrzeć do poniższej lekcji:
Aby zrozumieć istotę problemu, przeanalizujmy następujący dylemat. Mamy jakiś czworokąt, którego boki mają długość \(4, 5, 6\) oraz \(7\). Obok niego mamy drugi czworokąt, w którym wszystkie boki są dwa razy dłuższe, czyli mają miarę \(8, 10, 12\) oraz \(14\). Pytanie brzmi – czy te czworokąty są podobne? No właśnie, nie możemy tego jednoznacznie określić, bo choć stosunek długości boków jest ten sam (wszystkie boki drugiej figury są dwa razy większe od pierwszej), to jednak nic nie wiemy na temat kątów, a te mogą być zupełnie różne w jednej i drugiej figurze. Bardzo dobrze widać to na przykładzie kwadratu oraz rombu. Kwadrat o boku \(10\) nie będzie figurą podobną do rombu o boku \(5\), bo figury te będą mieć zupełnie inne kąty (o ile oczywiście romb nie jest kwadratem).
Gdyby jednak ten dylemat przenieść do środowiska trójkątów, to okaże się, że tutaj ten problem nie wystąpi. Jeżeli mamy trójkąt o bokach \(4, 5\) oraz \(6\), a obok niego znajdzie się trójkąt o bokach dwa razy większych, czyli \(8, 10\) oraz \(12\), to jesteśmy w stanie stwierdzić, że te figury są jak najbardziej podobne, nawet bez informacji na temat kątów. Wynika to wprost z jednej z trzech cech podobieństwa trójkątów, które teraz sobie omówimy.
Cechy podobieństwa trójkątów
Wyróżniamy trzy kluczowe cechy podobieństwa trójkątów. Omówmy osobno każdą z nich:
· cecha kąt-kąt-kąt (kkk)
Jeśli miary wszystkich kątów jednego trójkąta są takie same jak miary kątów drugiego trójkąta, to te trójkąty są podobne. Na poniższym rysunku mamy dwa trójkąty o kątach \(\alpha, \beta, \gamma\) i na tej podstawie możemy stwierdzić, że będą to trójkąty podobne:
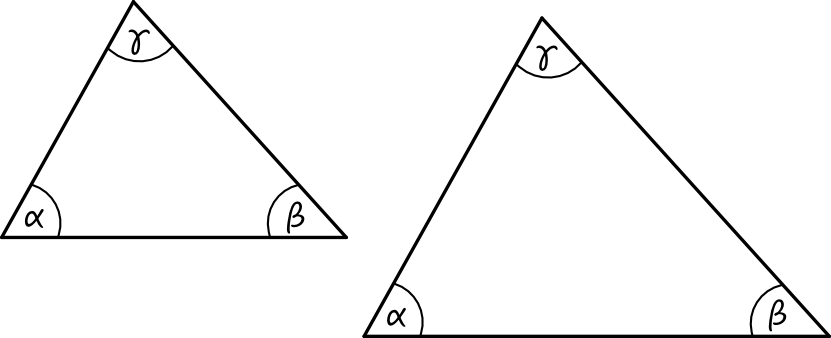
Z praktycznego punktu widzenia, moglibyśmy nawet ulepszyć tę regułę i dodać, że wystarczy aby w jednym i drugim trójkącie pokrywały się miary jedynie dwóch kątów. Dlaczego? Jeśli pokrywają nam się miary dwóch kątów, to i trzeci kąt będzie jednakowy, bo suma wszystkich kątów w trójkącie jest zawsze stała i wynosi \(180°\). Przykładowo, jeśli wiemy, że jeden i drugi trójkąt mają kąty o mierze \(50°\) oraz \(60°\), to i trzeci kąt w tych trójkątach będzie miał tą samą miarę, równą w tym przypadku \(180°-50°-60°=70°\). Z tego też względu ta cecha kąt-kąt-kąt jest często nazywana jako kąt-kąt.
· cecha bok-kąt-bok (bkb)
Jeśli długości dwóch boków jednego trójkąta są proporcjonalne do długości odpowiadających boków drugiego trójkąta, a kąt między tymi bokami jest w obydwu trójkątach jednakowy, to te trójkąty są podobne. Przykładem zastosowania tej cechy będzie taka oto sytuacja:
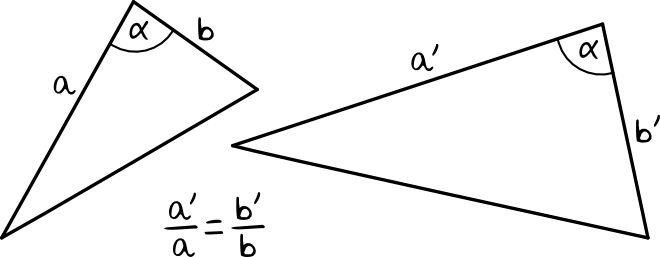
Mówiąc obrazowo – jeśli ustalimy, że dwa dowolne boki drugiego trójkąta są tyle samo razy większe lub mniejsze od pierwszego trójkąta, a kąt między tymi bokami będzie jednakowej miary, to trójkąty na pewno będą podobne.
· cecha bok-bok-bok (bbb)
Jeśli długości wszystkich boków jednego trójkąta są proporcjonalne do długości boków drugiego trójkąta, to trójkąty są podobne.
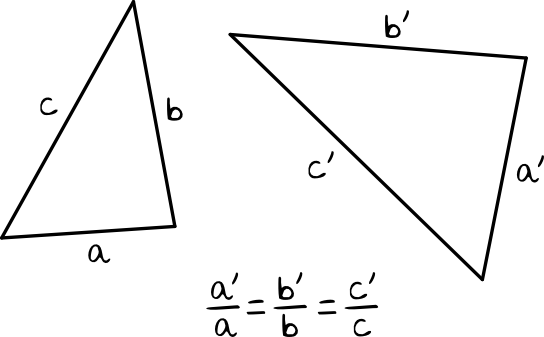
To właśnie z tej cechy korzystaliśmy pokazując sobie przykładowy dylemat we wstępie do tej lekcji. Jeśli wszystkie boki drugiego trójkąta są tyle samo razy większe lub mniejsze co trójkąta pierwszego, to trójkąty te są podobne.
Sprawdźmy teraz na przykładowych zadaniach, jak będzie wyglądać wykorzystanie tej wiedzy w praktyce.
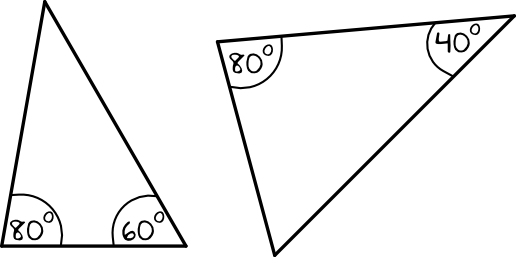
Rozwiązanie:
Na pierwszy rzut oka wydaje się, że kąty w tych trójkątach są różne, co mogłoby sugerować, że te trójkąty na pewno nie są podobne. Jak się za chwilę okaże, będzie to dość mylny trop. Zanim wykluczymy podobieństwo trójkątów, obliczmy miarę trzeciego kąta w pierwszym trójkącie. Suma kątów w trójkącie jest równa zawsze \(180°\), zatem trzeci kąt pierwszego trójkąta ma miarę:
$$180°-80°-60°=40°$$
Miary trzeciego kąta w drugim trójkącie już obliczać nie musimy, widzimy wyraźnie, że w jednym i drugim trójkącie są dwie jednakowe miary kątów, więc możemy od razu stwierdzić, że jeden i drugi trójkąt to będą trójkąty o miarach kątów \(40°, 60°\) oraz \(80°\). Możemy więc stwierdzić, że te trójkąty są podobne na podstawie cechy kąt-kąt-kąt.
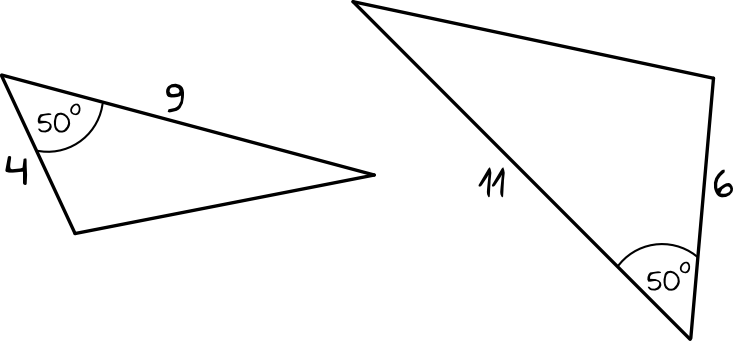
Rozwiązanie:
Tu powinniśmy dostrzec, że kluczowa dla nas będzie cecha bok-kąt-bok, ponieważ mamy jednakowy kąt w obydwu trójkątach i znamy miarę boków, które ten kąt tworzą. W pierwszym trójkącie krótszy z boków ma długość \(4\), a w drugim \(6\), czyli ten drugi trójkąt ma długość odpowiadającego boku \(1,5\) razy większą. Precyzyjnie rzecz ujmując moglibyśmy nawet stwierdzić, że skala podobieństwa figur to \(k=1,5\). W przypadku dłuższego boku pierwszy trójkąt ma miarę \(9\), a drugi \(11\), czyli nie jest to miara \(1,5\) razy większa. To oznacza, że te trójkąty nie są podobne.
Umiejętność określania podobieństwa figur pozwoli nam rozwiązywać nieco bardziej rozbudowane zadania z geometrii. Co ciekawe, mogą to być także zadania związane z innymi figurami niż trójkąty.
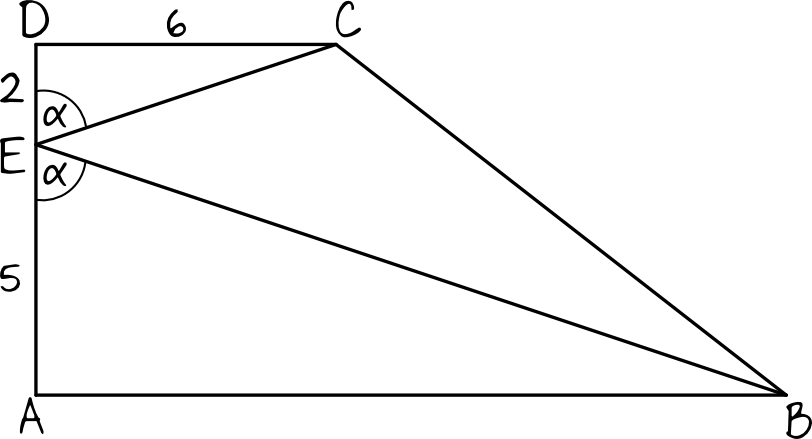
Rozwiązanie:
Pole trapezu obliczamy ze wzoru \(P=\frac{1}{2}(a+b)\cdot h\). Spoglądając na dane z rysunku widzimy, że tak naprawdę brakuje nam tylko znajomości długości dolnej podstawy \(AB\).
Kluczem do sukcesu będzie dostrzeżenie, że trójkąty \(ABE\) oraz \(ECD\) są podobne. Skąd to wiemy? Skoro jest to trapez prostokątny, to obydwa te trójkąty są prostokątne (kąt prosty przy wierzchołku \(A\) oraz \(D\)). Wiemy też, że obydwa te trójkąty mają jednakowy kąt o mierze \(\alpha\). To prowadzi nas do wniosku, że w jednym i drugim trójkącie mamy kąty o tej samej mierze, czyli na podstawie cechy kąt-kąt-kąt możemy stwierdzić że są to trójkąty podobne.
To obliczmy teraz skalę podobieństwa tych trójkątów. Aby się nie pogubić, możemy przyjąć, że trójkąt \(ECD\) jest podstawowym, a trójkąt \(ABE\) podobnym. Bokami odpowiadającymi o znanej mierze będą boki \(AE\) oraz \(DE\), zatem moglibyśmy zapisać, że:
$$k=\frac{|AE|}{|DE|} \\
k=\frac{5}{2}=2,5$$
Wyszło nam więc, że wszystkie boki trójkąta \(ABE\) są \(2,5\) razy większe od boków trójkąta \(ECD\), a to z kolei prowadzi nas do wniosku, że tym samym podstawa \(AB\) będzie \(2,5\) razy większa od boku \(DC\). Zapisalibyśmy więc, że:
$$|AB|=k\cdot|DC| \\
|AB|=2,5\cdot6 \\
|AB|=15$$
Skoro tak, to pole naszego trapezu wyniesie:
$$P=\frac{1}{2}\cdot(15+6)\cdot 7 \\
P=\frac{1}{2}\cdot21\cdot7 \\
P=73,5$$
Tak na marginesie, długość podstawy \(AB\) można byłoby wyznaczyć w jeszcze inny sposób. Skoro są to trójkąty podobne i skoro dłuższa przyprostokątna trójkąta \(ECD\) ma miarę \(3\) razy większą od krótszej przyprostokątnej, to tak samo będzie też w trójkącie \(ABE\), co doprowadzi nas do wniosku, że \(|AB|=3\cdot5=15\). To podejście też jest jak najbardziej poprawne.
Zobacz także:
