Rozwiązanie
Wprowadźmy sobie kilka oznaczeń i zaznaczmy odpowiednie kąty:
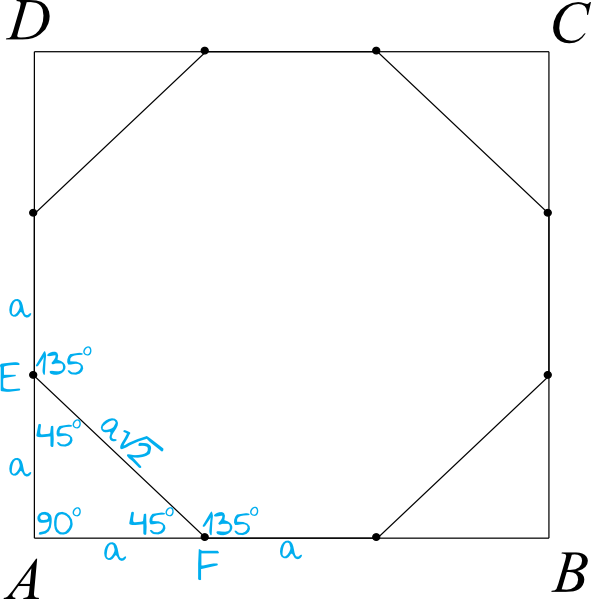
Trójkąt \(AEF\) (oraz pozostałe trójkąty w rogach) są na pewno trójkątami równoramiennymi prostokątnymi, stąd też wiemy że kąty ostre w tych trójkątach mają miarę \(45°\).
Idąc dalej, możemy zauważyć że powstały nam pary kątów przyległych. Skoro suma kątów przyległych ma być równa \(180°\), to kąty przyległe do kątów o mierze \(45°\) muszą mieć \(180°-45°=135°\), co zostało oznaczone na rysunku.
To oznacza, że prawidłowa będzie trzecia odpowiedź, czyli że każdy kąt wewnętrzny ośmiokąta ma miarę \(135°\).
Przy okazji warto wyjaśnić sobie skąd wiemy, że pozostałe odpowiedzi są błędne. Jeżeli oznaczymy sobie odcinki \(AE\) oraz \(AF\) jako \(a\), to z własności trójkątów \(90°, 45°, 45°\) wynika, że odcinek \(EF\) ma długość \(a\sqrt{2}\). Wyraźnie więc widzimy, że w ośmiokącie są różne długości boków. To wyklucza więc odpowiedzi A (bo ośmiokąt foremny musi mieć jednakowe długości boków), wyklucza to też odpowiedź B i wyklucza to odpowiedź D, bowiem \(a\sqrt{2}\lt a+a\).