Rozwiązanie
Krok 1. Obliczenie długości boku rombu.
Z własności rombów wiemy, że przekątne rombu przecinają się pod kątem prostym w połowie swojej długości. To oznacza, że otrzymamy następującą sytuację:
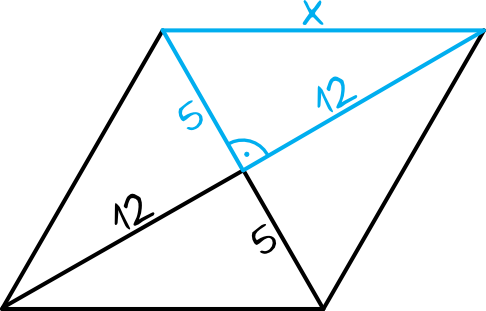
Powstały nam na rysunku trójkąty prostokątne z których możemy obliczyć długość boku rombu. Korzystając z Twierdzenia Pitagorasa możemy zapisać, że:
$$5^2+12^2=x^2 \\
25+144=x^2 \\
x^2=169 \\
x=13 \quad\lor\quad x=-13$$
Bok rombu jest na pewno liczbą dodatnią, zatem zostaje nam \(x=13\).
Krok 2. Obliczenie wysokości ostrosłupa.
Z treści zadania wynika, że ostrosłup ma wysokość dwa razy dłuższą od boku rombu. Skoro więc bok rombu miał długość \(13cm\), to wysokość będzie równa:
$$H=2\cdot13cm \\
H=26cm$$
Krok 3. Obliczenie pola podstawy ostrosłupa.
Znamy długości przekątnych rombu, zatem możemy bez przeszkód obliczyć jego pole powierzchni, które jednocześnie będzie polem podstawy ostrosłupa:
$$P_{p}=\frac{1}{2}ef \\
P_{p}=\frac{1}{2}\cdot10\cdot24 \\
P_{p}=5\cdot24 \\
P_{p}=120[cm^2]$$
Krok 4. Obliczenie objętości ostrosłupa.
Wiemy już, że \(P_{p}=120cm^2\) oraz że \(H=26cm\), zatem objętość ostrosłupa będzie równa:
$$V=\frac{1}{3}P_{p}\cdot H \\
V=\frac{1}{3}\cdot120cm^2\cdot26cm \\
V=40cm^2\cdot26cm \\
V=1040cm^3$$