Rozwiązanie
Krok 1. Obliczenie długości krawędzi pojedynczej kostki.
Skoro sześcian o krawędzi długości \(30cm\) podzielono dokładnie tak jak przedstawia to rysunek, to każda mała kostka ma wymiary \(10cm\times10cm\times10cm\).
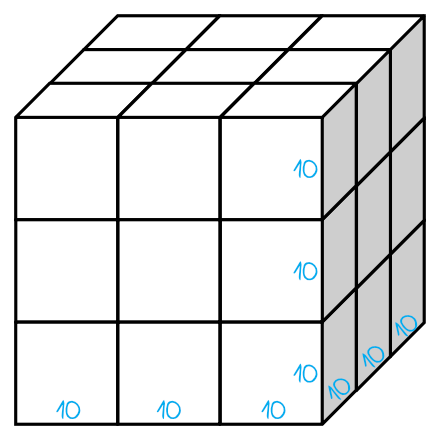
Krok 2. Ocena prawdziwości pierwszego zdania.
Z ośmiu kostek możemy złożyć następujący sześcian:
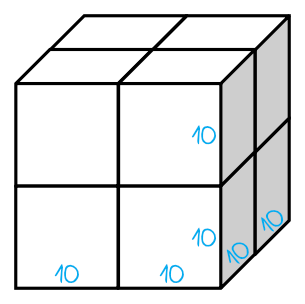
Widzimy więc, że jest to sześcian o boku \(20cm\). To oznacza, że jego pole powierzchni będzie równe:
$$P_{c}=6a^2 \\
P_{c}=6\cdot20^2 \\
P_{c}=6\cdot400 \\
P_{c}=2400[cm^2]$$
Pierwsze zdanie jest więc nieprawdą.
Krok 3. Ocena prawdziwości drugiego zdania.
Korzystamy z tego samego sześcianu co w kroku drugim. Jego objętość będzie równa:
$$V=a^3 \\
V=20^3 \\
V=8000[cm^3]$$
Drugie zdanie jest więc prawdą.