Rozwiązanie
Krok 1. Sporządzenie rysunku pomocniczego.
Spróbujmy rozpisać długości krawędzi ostrosłupa \(EFGB\). Z własności kwadratów wiemy, że kwadrat o boku \(a\) ma przekątną o długości \(a\sqrt{2}\). Skoro tak, to krawędzie \(BE\), \(BG\) oraz \(EG\) będą miały właśnie długość \(a\sqrt{2}\).
Oprócz tego musimy dostrzec, że krawędzie \(BF\), \(EF\) oraz \(FG\) mają długość \(a\). Sytuacja będzie więc wyglądać następująco:
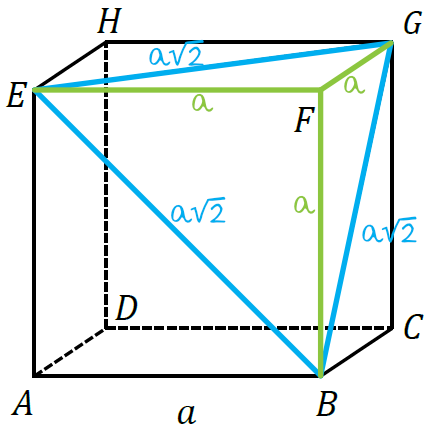
To prowadzi nas do wniosku, że na pole powierzchni całkowitej składać się będzie podstawa, która jest trójkątem równobocznym o boku \(a\sqrt{2}\) oraz trzy ściany boczne, które są trójkątami prostokątnymi o przyprostokątnych długości \(a\).
Krok 2. Obliczenie pola powierzchni podstawy.
Pole trójkąta równobocznego znajdującego się w podstawie zapiszemy jako
$$P_{p}=\frac{(a\sqrt{2})^2\sqrt{3}}{4} \\
P_{p}=\frac{a^2\cdot2\cdot\sqrt{3}}{4} \\
P_{p}=\frac{a^2\sqrt{3}}{2}$$
Krok 3. Obliczenie pola powierzchni bocznej.
Pole powierzchni bocznej tworzą trzy trójkąty prostokątne o przyprostokątnych \(a\). Możemy więc zapisać, że:
$$P_{b}=3\cdot\frac{1}{2}ah \\
P_{b}=3\cdot\frac{1}{2}\cdot a\cdot a \\
P_{b}=\frac{3}{2}\cdot a^2$$
Krok 4. Obliczenie pola powierzchni całkowitej.
Mając obliczone \(P_{p}\) oraz \(P_{b}\) możemy zapisać, że:
$$P_{c}=\frac{a^2\sqrt{3}}{2}+\frac{3}{2}\cdot a^2 \\
P_{c}=\frac{\sqrt{3}}{2}\cdot a^2+\frac{3}{2}\cdot a^2 \\
P_{c}=\frac{\sqrt{3}+3}{2}\cdot a^2 \\
P_{c}=\frac{3+\sqrt{3}}{2}\cdot a^2$$