Funkcje

Funkcje to jeden z największych działów na matematyce, a dobre zrozumienie tego zagadnienia pomaga w opanowaniu kolejnych działów. Powiedzmy sobie zatem czym są funkcje, o co w nich chodzi i jak je możemy opisywać?

Co to jest funkcja?
Funkcją matematyczną nazywamy przyporządkowanie każdemu elementowi zbioru \(x\) dokładnie jednego elementu zbioru \(y\). Fachowo na matematyce zbiór iksów nazywać będzie argumentami funkcji, natomiast zbiór igreków wartościami funkcji. Ta definicja brzmi skomplikowania, dlatego aby lepiej zrozumieć istotę funkcji to pokażmy to sobie na konkretnych przykładach:
• Jeżeli każdemu dziecku przyporządkujemy liczbę mówiącą o tym ile centymetrów ma wzrostu, to będzie to funkcja – bo jednemu dziecku przyporządkujemy jedną liczbę np. Jaś-170, Małgosia-160 itd.
• Jeżeli każdemu dziecku przyporządkujemy liczbę mówiącą o tym ile ma rodzeństwa, to będzie to funkcja – bo jednemu dziecku przyporządkujemy jedną liczbę np. Jaś-3, Małgosia-0.
• Jeżeli każdemu dziecku przyporządkujemy liczbę mówiącą o tym jaką ma na świadectwie ocenę z matematyki, to będzie to funkcja – bo jednemu dziecku przyporządkowujemy jedną liczbę np. Jaś-5, Małgosia-5 (zwróć uwagę, że możemy dwóm różnym uczniom (argumentom) możemy przyporządkować te same oceny (wartości)).

A co nie będzie funkcją?
• Jeżeli do poszczególnych pomiarów wzrostu przyporządkujemy imiona dzieci, to nie będzie to funkcja – bo pomiar np. 160cm może mieć kilku uczniów.
• Jeżeli do liczby rodzeństwa przyporządkujemy imiona dzieci, to nie będzie to funkcja – bo np. dwójkę rodzeństwa może mieć kilka osób.
• Jeżeli każdemu dziecku przyporządkujemy zdobyte oceny ze wszystkich przedmiotów, to nie będzie to funkcja – bo jedno dziecko będzie miało więcej niż jedną ocenę np. Jaś-5-4-3-4-2, Małgosia-3-4-6-6-5.

Z tego płyną dla nas dwa główne wnioski:
1. Jeden argument \(x\) ma jedną odpowiadająca mu wartość \(y\).
2. Argumenty \(x\) są niepowtarzalne, wartości \(y\) mogą się powtórzyć.

Nas na matematyce oczywiście będą interesować przede wszystkim te funkcje, które da się opisać liczbami, a najlepiej kiedy da się opisać je jakimiś zależnościami, które zapiszemy później w formie wzoru.

Różne formy prezentacji funkcji
Funkcje możemy zobrazować na cztery sposoby:
a) graf – nie jest to może zbyt popularna forma prezentacji funkcji, ale świetnie obrazuje to czym są funkcje. Każdemu elementowi z lewego zbioru przyporządkowana jest jakaś wartość ze zbioru drugiego. Przykładowy graf wyglądałby następująco:

Zwróć uwagę na to, że każdej liczbie ze zbioru argumentów \(x\) przyporządkowana jest jakaś wartość \(y\) i może się zdarzyć, że dla dwóch rożnych argumentów przyporządkowana będzie ta sama wartość.

b) tabelka – często jest wykorzystywana do rysowania wykresów funkcji. Na górze tabelki wypisujemy argumenty funkcji (czyli iksy), a na dole odpowiadające tym argumentom wartości (czyli igreki).

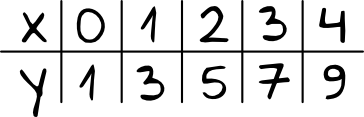
c) wykres – jest to prezentacja graficzna funkcji w układzie współrzędnych. Do narysowania wykresów takich funkcji często będziemy wyznaczać współrzędne charakterystycznych punktów, które do tej funkcji należą.

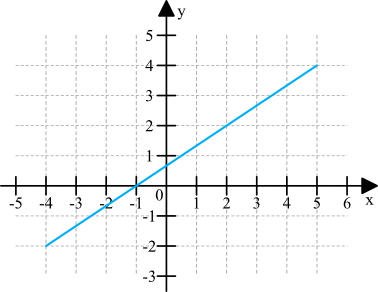
d) wzór – zdecydowanie najlepszy i najbardziej popularny sposób prezentacji funkcji. Przewagą wzoru nad innymi postaciami jest to, że dzięki wzorom możemy w prosty sposób poznać dowolne wartości funkcji dla dowolnych argumentów. Bardzo często też ze wzoru będziemy odczytywać lub obliczać kluczowe informacje na temat funkcji (np. czy jest rosnąca, gdzie ma miejsca zerowe, gdzie przecina się z osią igreków itd.). Wzory funkcji zapisujemy w postaci np.:
$$f(x)=x+5 \\
\text{lub } y=x+5$$

Więcej informacji na temat funkcji znajdziesz w poniższych tematach:

O funkcjach liniowych przeczytasz tutaj:

Informacje na temat funkcji kwadratowej znajdziesz tutaj: