Ostrosłupy - zadania (egzamin ósmoklasisty)
Zadanie 3. (1pkt) Siatka ostrosłupa składa się z kwadratu i trójkątów równobocznych zbudowanych na bokach tego kwadratu.
Oceń prawdziwość podanych zdań.
Wszystkie krawędzie tego ostrosłupa mają taką samą długość.
Wysokość tego ostrosłupa jest mniejsza niż wysokość jego ściany bocznej.
Odpowiedź
1) PRAWDA
2) PRAWDA
Wyjaśnienie:
Krok 1. Ocena prawdziwości pierwszego zdania.
Pierwsze zdanie jest prawdą. Skoro wszystkie trójkąty są równoboczne, to wszystkie krawędzie ostrosłupa będą mieć taką samą długość.
Krok 2. Ocena prawdziwości drugiego zdania.
Drugie zdanie jest prawdą. Wszystko wyjaśni poniższy rysunek:
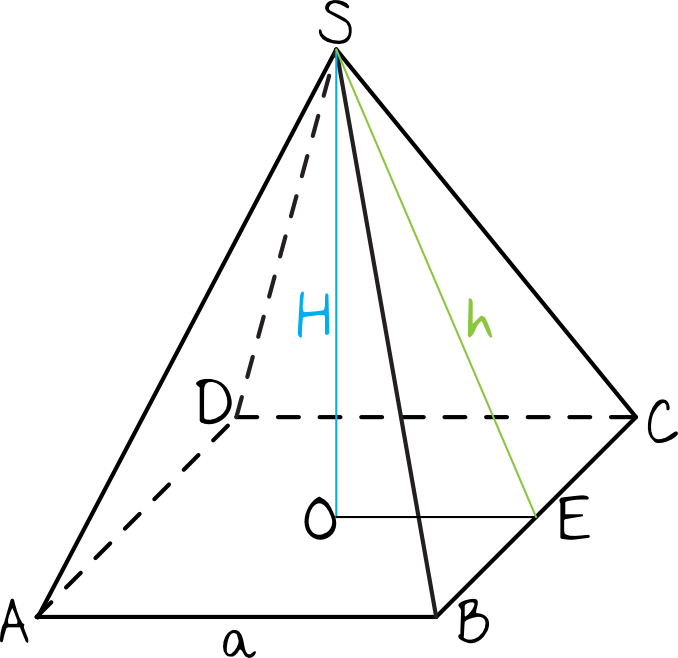
Z rysunku wynika, że możemy wyodrębnić trójkąt prostokątny w którym przyprostokątną jest wysokość graniastosłupa, a przeciwprostokątną jest wysokość ściany bocznej. Z racji tego iż w trójkątach prostokątnych przyprostokątne są zawsze krótsze od przeciwprostokątnej, to faktycznie wysokość ostrosłupa będzie mniejsza niż wysokość jego ściany bocznej.
Zadanie 4. (1pkt) Maciek rysuje siatkę ostrosłupa prawidłowego, którego podstawą jest kwadrat o środku w punkcie \(O\) i boku długości \(8\).
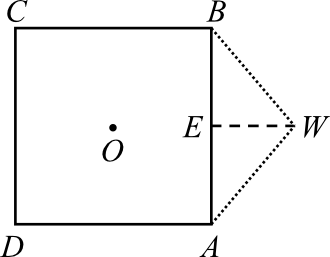
Czy trójkąt \(ABW\) o bokach długości odpowiednio: \(8, 5, 5\) może być ścianą boczną takiego ostrosłupa?
trójkąt \(ABW\) jest równoramienny
odległość \(OE\) jest mniejsza niż wysokość \(EW\) trójkąta \(ABW\)
odległość \(OE\) jest większa niż wysokość \(EW\) trójkąta \(ABW\)
Wyjaśnienie:
Krok 1. Obliczenie długości \(EW\).
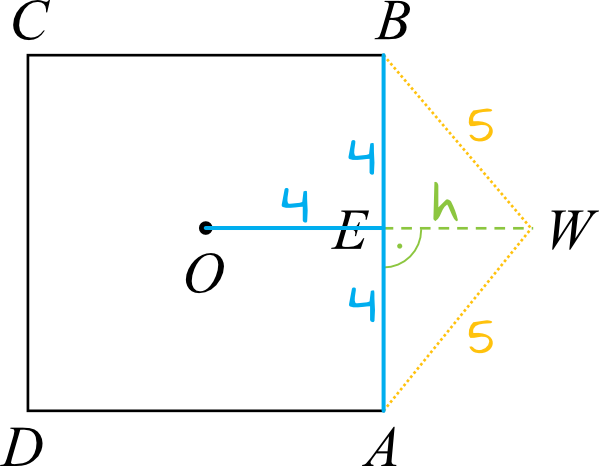
Aby obliczyć długość odcinka \(EW\) musimy posłużyć się Twierdzeniem Pitagorasa:
$$4^2+|EW|^2=5^2 \\
16+|EW|^2=25 \\
|EW|^2=9 \\
|EW|=3$$
Krok 2. Obliczenie długości odcinka \(OE\).
Odcinek \(OE\) ma długość równą połowie boku kwadratu, czyli \(OE=4\).
Krok 3. Interpretacja otrzymanego wyniku.
Gdyby kawałek naszej siatki pokazać na rysunku ostrosłupa, to otrzymalibyśmy mniej więcej coś takiego:
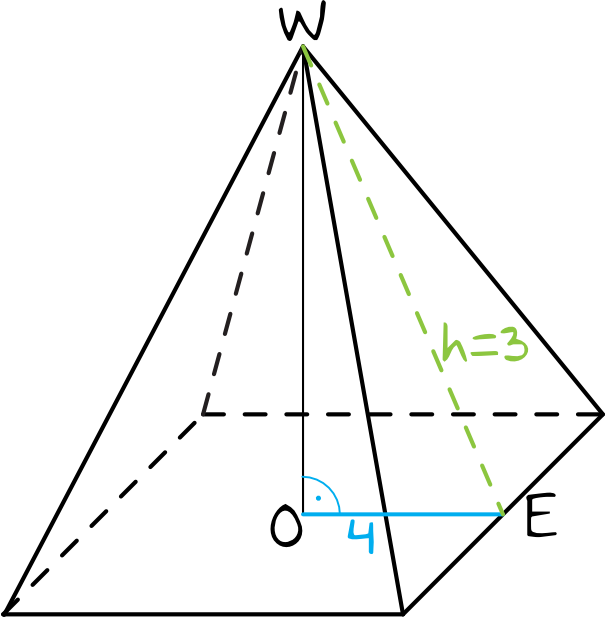
Spójrzmy na trójkąt prostokątny \(OEW\). W trójkątach prostokątnych najdłuższym bokiem jest zawsze przeciwprostokątna. W tym przypadku, po złożeniu siatki tak się nie stało, bo przeciwprostokątną jest odcinek \(EW=3\), a dolna przyprostokątna ma długość \(OE=4\), co stoi w sprzeczności z zasadami budowy trójkątów prostokątnych. To właśnie ta informacja oznacza, że taki ostrosłup jest po prostu niemożliwy do stworzenia.
Zadanie 6. (4pkt) Pole powierzchni bocznej ostrosłupa prawidłowego czworokątnego jest równe \(80cm^2\), a pole jego powierzchni całkowitej wynosi \(144cm^2\). Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa.
Odpowiedź
Długość krawędzi podstawy jest równa \(8cm\), natomiast długość krawędzi bocznej ma miarę \(\sqrt{41}cm\).
Wyjaśnienie:
Krok 1. Sporządzenie rysunku pomocniczego.
Narysujmy sobie ten ostrosłup i zaznaczmy w nim najistotniejsze długości które potem przydadzą nam się do obliczenia pożądanych wartości.
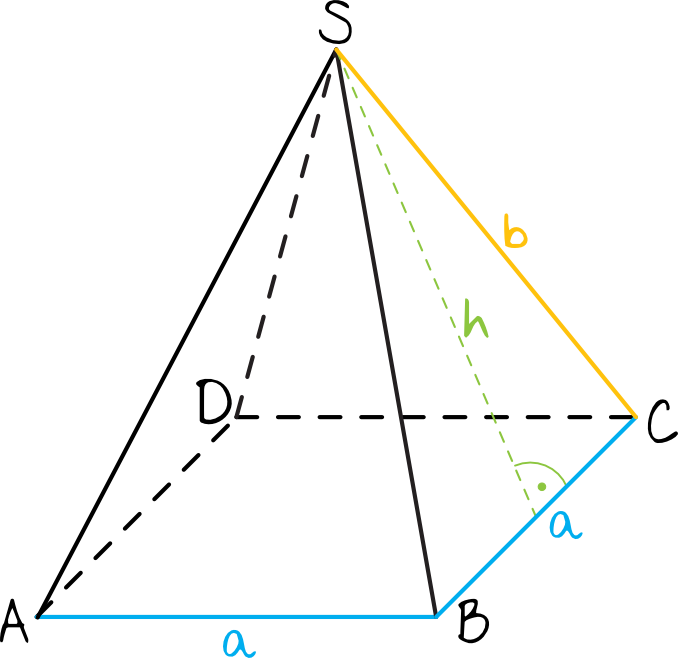
Krok 2. Obliczenie pola podstawy.
Skoro pole powierzchni całkowitej wynosi \(144cm^2\) z czego pole powierzchni bocznej jest równe \(80cm^2\), to znaczy że pole podstawy jest równe:
$$144cm^2-80cm^2=64cm^2$$
Krok 3. Obliczenie krawędzi podstawy.
Z treści zadania wiemy, że jest to ostrosłup prawidłowy czworokątny, a skoro tak, to w jego podstawie znajduje się kwadrat. My o tym kwadracie wiemy już to, że jego pole powierzchni jest równe \(64cm^2\), zatem krawędź tego kwadratu ma długość:
$$P=a^2 \\
64cm^2=a^2 \\
a=8cm$$
Krok 4. Obliczenie wysokości ściany bocznej.
Spróbujmy teraz obliczyć wysokość trójkąta znajdującego się w ścianie bocznej ostrosłupa. Wiemy, że pole powierzchni bocznej jest równe \(80cm^2\), a skoro powierzchnię boczną tworzą cztery jednakowe trójkąty, to każdy z nich ma pole powierzchni równe:
$$80cm^2:4=20cm^2$$
Wiemy więc, że trójkąt będący ścianą boczną ma długość podstawy \(a=8cm\), wiemy też że jego pole powierzchni jest równe \(20cm^2\), więc bez przeszkód obliczymy wysokość tego trójkąta.
$$P=\frac{1}{2}ah \\
20cm^2=\frac{1}{2}\cdot8cm\cdot h \\
20cm^2=4cm\cdot h \\
h=5cm$$
Krok 5. Obliczenie długości krawędzi bocznej ostrosłupa.
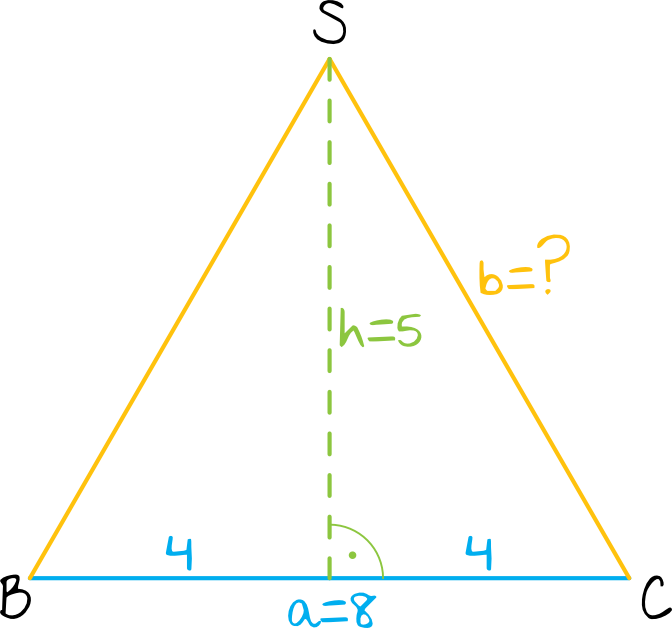
W ścianach bocznych naszego ostrosłupa znajdują się trójkąty równoramienne, więc wysokość podzieliła nam podstawę na dwie równe części. To pozwala nam na obliczenie długości krawędzi bocznej (czyli długości \(b\)) za pomocą Twierdzenia Pitagorasa:
$$4^2+5^2=b^2 \\
16+25=b^2 \\
b^2=41 \\
b=\sqrt{41}[cm]$$
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz długość krawędzi ostrosłupa (Krok 3.).
ALBO
• Gdy obliczysz pole powierzchni pojedynczej ściany bocznej ostrosłupa (Krok 4.).
2 pkt
• Gdy obliczysz wysokość ściany bocznej ostrosłupa (Krok 4.).
3 pkt
• Gdy obliczysz wszystkie elementy zadania, ale otrzymasz błędny wynik ze względu na błąd rachunkowy.
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Zadanie 7. (5pkt) Na sąsiednich działkach wybudowano domy różniące się kształtem dachów (patrz rysunki). Który dach ma większą powierzchnię?
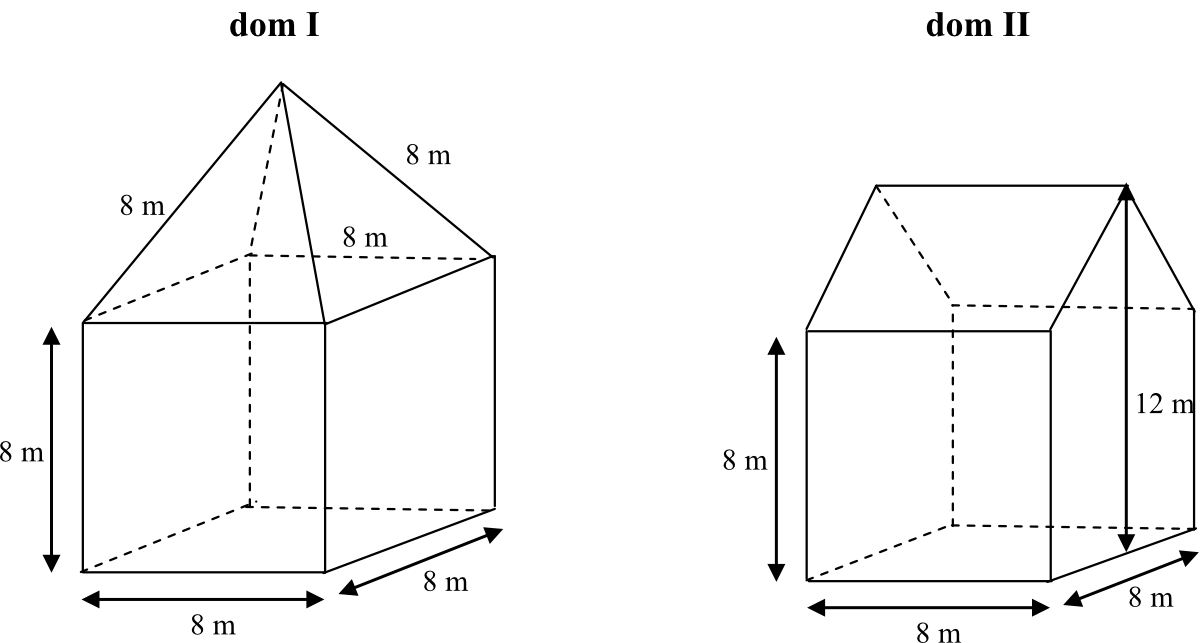
Odpowiedź
Większe pole powierzchni ma pierwszy dach.
Wyjaśnienie:
Krok 1. Obliczenie pola powierzchni pierwszego dachu.
Zacznijmy od obliczenia pola powierzchni pierwszego dachu. Dach składa się z czterech trójkątów równobocznych o boku długości \(8cm\). Musimy więc wyznaczyć pole każdego takiego trójkąta i pomnożyć to przez \(4\). Wyznaczyć pole tego trójkąta można tak naprawdę na dwa sposoby:
I sposób - korzystając ze wzoru na pole trójkąta równobocznego.
Wzór na pole trójkąta równobocznego jest następujący:
$$P=\frac{a^2\sqrt{3}}{4} \\
P=\frac{8^2\sqrt{3}}{4} \\
P=\frac{64\sqrt{3}}{4} \\
P=16\sqrt{3}$$
Skoro mamy cztery takie trójkąty, to pole powierzchni dachu będzie równe:
$$P_{1}=4\cdot16\sqrt{3}=64\sqrt{3}$$
II sposób - wyznaczając wysokość trójkąta równobocznego.
Tym razem możemy skorzystać ze wzoru na wysokość trójkąta równobocznego:
$$h=\frac{a\sqrt{3}}{2} \\
h=\frac{8\sqrt{3}}{2} \\
h=4\sqrt{3}$$
Jeśli tego wzoru nie pamiętamy, to ostatecznie możemy wyznaczyć wysokość z Twierdzenia Pitagorasa, wiedząc że wysokość trójkąta równobocznego dzieli podstawę na dwie równe części:
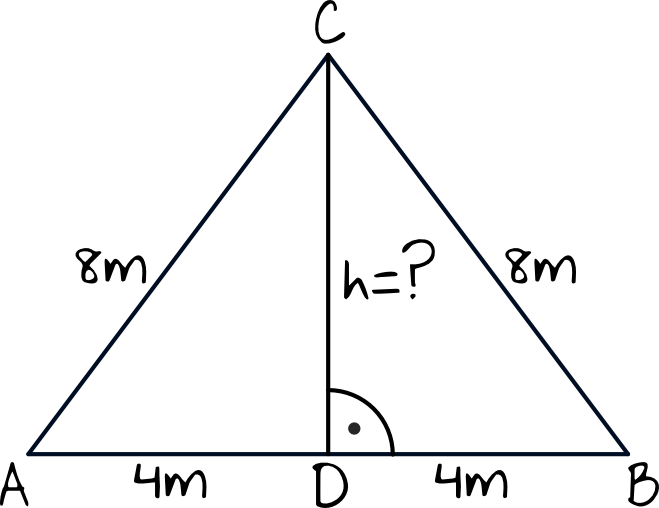
$$4^2+h^2=8^2 \\
16+h^2=64 \\
h^2=48 \\
h=\sqrt{48}=4\sqrt{3}$$
Znając wysokość trójkąta równobocznego możemy obliczyć już bez przeszkód jego pole standardowym wzorem na pole trójkąta:
$$P=\frac{1}{2}ah \\
P=\frac{1}{2}\cdot8\cdot4\sqrt{3} \\
P=4\cdot4\sqrt{3} \\
P=16\sqrt{3}$$
Skoro mamy cztery takie trójkąty, to pole powierzchni dachu będzie równe:
$$P_{1}=4\cdot16\sqrt{3}=64\sqrt{3}$$
Krok 2. Obliczenie pola powierzchni drugiego dachu.
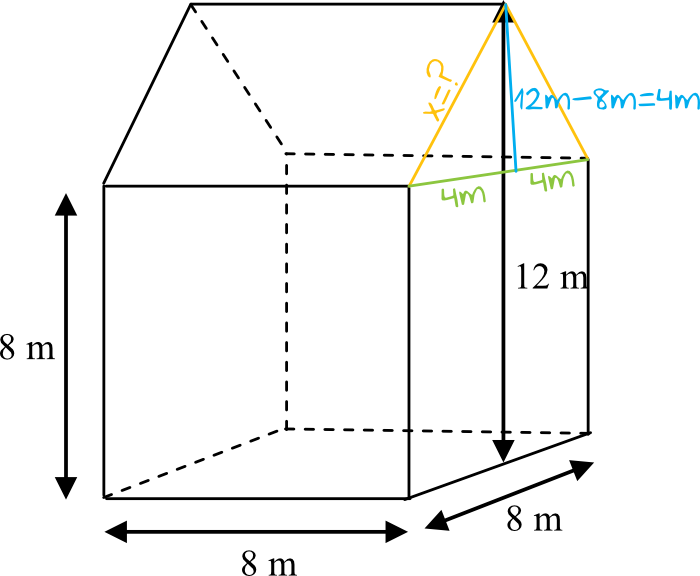
Do obliczenia pola powierzchni drugiego dachu (składającego się z dwóch prostokątów) potrzebujemy znać długość krótszego boku prostokąta. Obliczymy go z Twierdzenia Pitagorasa i trójkąta zaznaczonego na powyższym rysunku:
$$4^2+4^2=x^2 \\
16+16=x^2 \\
x^2=32 \\
x=\sqrt{32}=4\sqrt{2}$$
W związku z tym pojedynczy kawałek dachu jest prostokątem o wymiarach \(8\times4\sqrt{2}\), zatem jego pole powierzchni będzie równe:
$$P=8\cdot4\sqrt{2} \\
P=32\sqrt{2}$$
Nasz drugi dach składa się z dwóch takich prostokątów, zatem jego pole powierzchni będzie równe:
$$P_{2}=2\cdot32\sqrt{2} \\
P_{2}=64\sqrt{2}$$
Krok 3. Określenie który dach ma większą powierzchnię.
Pierwszy dach ma powierzchnię \(64\sqrt{3}\), drugi dach ma powierzchnię \(64\sqrt{2}\), zatem to pierwszy dach ma tę powierzchnię większą:
$$64\sqrt{3}\gt64\sqrt{2} \\
P_{1}\gt P_{2}$$
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz wysokość trójkąta będącego częścią pierwszego dachu \(h=4\sqrt{3}\) (Krok 1. II sposób).
ALBO
• Gdy obliczysz długość krótszego boku prostokąta będącego częścią drugiego dachu \(x=\sqrt{32}=4\sqrt{2}\) (Krok 2.).
2 pkt
• Gdy obliczysz pole powierzchni pierwszego dachu (Krok 1.).
ALBO
• Gdy obliczysz pole powierzchni drugiego dachu (Krok 2.).
3 pkt
• Gdy obliczysz pole powierzchni jednego z dwóch dachów oraz obliczysz kluczowy wymiar następnego dachu, czyli \(h=4\sqrt{3}\) dla pierwszego dachu lub \(x=\sqrt{32}=4\sqrt{2}\) dla drugiego dachu (Krok 1. i 2.).
4 pkt
• Gdy obliczysz pole powierzchni obydwu dachów (Krok 1. i 2.) i na tym zakończysz rozwiązywanie lub też źle określisz który dach ma większą powierzchnię.
5 pkt
• Gdy otrzymasz oczekiwany wynik.
Zadanie 9. (1pkt) Na rysunkach przedstawiono ostrosłup prawidłowy i graniastosłup prawidłowy. Wszystkie krawędzie obu brył są jednakowej długości.

Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe.
Suma długości wszystkich krawędzi ostrosłupa jest większa niż suma długości wszystkich krawędzi graniastosłupa.
Całkowite pole powierzchni ostrosłupa jest większe niż całkowite pole powierzchni graniastosłupa.
Odpowiedź
1) FAŁSZ
2) FAŁSZ
Wyjaśnienie:
Krok 1. Ocena prawdziwości pierwszego zdania.
Ostrosłup ma \(8\) krawędzi, natomiast graniastosłup ma \(9\) krawędzi. Skoro każda z krawędzi ma jednakową długość, to suma wszystkich krawędzi ostrosłupa jest na pewno mniejsza niż suma suma długości wszystkich krawędzi graniastosłupa. Zdanie jest więc fałszem.
Krok 2. Ocena prawdziwości drugiego zdania.
Skoro wszystkie krawędzie mają jednakową długość, to znaczy że ścianami tych brył są trójkąty równoboczne oraz kwadraty. W związku z tym musimy skorzystać ze wzorów na pole trójkąta równobocznego oraz kwadratu.
$$P_{tr}=\frac{a^2\sqrt{3}}{4} \\
P_{kw}=a^2$$
W ostrosłupie mamy cztery ściany trójkątne i jedną ścianę kwadratową, zatem pole powierzchni całkowitej ostrosłupa będzie równe:
$$P_{o}=4\cdot P_{tr}+P_{kw} \\
P_{o}=4\cdot\frac{a^2\sqrt{3}}{4}+a^2 \\
P_{o}=a^2\sqrt{3}+a^2$$
W graniastosłupie mamy dwie ściany trójkątne oraz trzy kwadratowe, zatem pole powierzchni całkowitej graniastosłupa będzie równe:
$$P_{g}=2\cdot P_{tr}+3\cdot P_{kw} \\
P_{g}=2\cdot\frac{a^2\sqrt{3}}{4}+3a^2 \\
P_{g}=\frac{a^2\sqrt{3}}{2}+3a^2$$
Teraz powinniśmy porównać do siebie pola powierzchni całkowitej ostrosłupa i graniastosłupa, ale tak na pierwszy rzut oka nie jesteśmy w stanie stwierdzić, które pole jest większe. Dlatego też w jednym i drugim polu powierzchni musimy jeszcze wyłączyć wspólny czynnik przed nawias:
$$P_{o}=a^2\sqrt{3}+a^2=a^2(\sqrt{3}+1) \\
P_{g}=3a^2+\frac{a^2\sqrt{3}}{2}=a^2\left(3+\frac{\sqrt{3}}{2}\right)$$
W tym momencie porównanie pól powierzchni robi się już znacznie łatwiejsze, bowiem przyjmując przybliżenie \(\sqrt{3}\approx1,73\) wyjdzie nam, że:
$$P_{o}\approx a^2\cdot(1,73+1)\approx 2,73a^2 \\
P_{g}\approx a^2\cdot\left(3+\frac{1,73}{2}\right)\approx3,865a^2$$
To oznacza, że pole ostrosłupa jest mniejsze niż pole graniastosłupa, zatem zdanie jest fałszem.
Zadanie 10. (1pkt) Na rysunku przedstawiono ostrosłup prawidłowy czworokątny i sześcian. Bryły mają jednakowe podstawy i równe wysokości, a suma objętości tych brył jest równa \(36cm^3\).
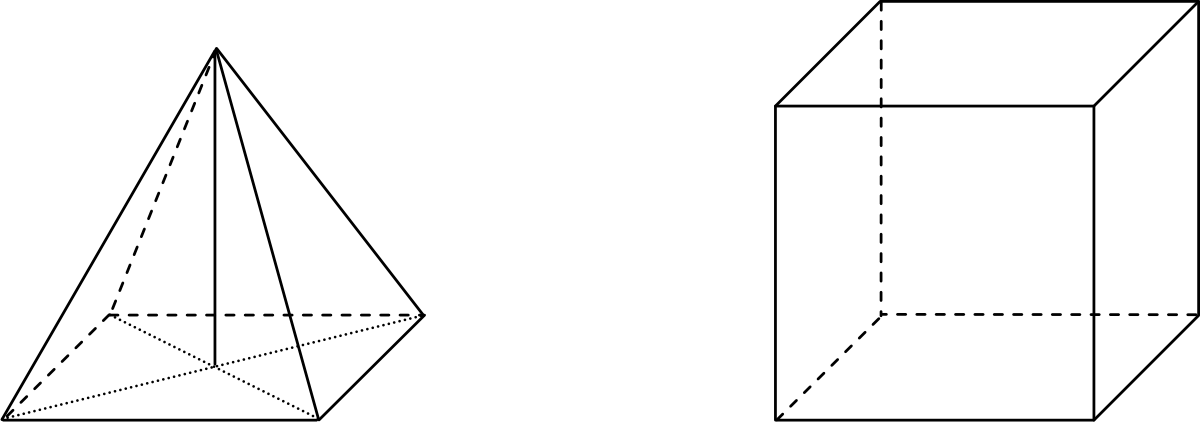
Oceń prawdziwość podanych zdań.
Objętość sześcianu jest trzy razy większa od objętości ostrosłupa.
Krawędź sześcianu ma długość \(3cm\).
Odpowiedź
1) PRAWDA
2) PRAWDA
Wyjaśnienie:
Krok 1. Ocena prawdziwości pierwszego zdania.
Zapiszmy sobie wzory na objętość ostrosłupa oraz sześcianu.
$$V_{ostrosłupa}=\frac{1}{3}P_{p}\cdot H \\
V_{sześcianu}=P_{p}\cdot H$$
Z treści zadania wiemy, że pola podstaw oraz wysokości są takie same w obydwu bryłach. Skoro tak, to faktycznie objętość sześcianu będzie trzykrotnie większa od objętości ostrosłupa, a wynika to wprost ze wzorów na objętość tych brył. To oznacza, że pierwsze zdanie jest prawdą.
Krok 2. Ocena prawdziwości drugiego zdania.
Suma objętości tych dwóch brył jest równa \(36cm^3\). W poprzednim kroku udowodniliśmy sobie, że objętość sześcianu będzie \(3\) razy większa od objętości ostrosłupa. Jeżeli więc objętość ostrosłupa oznaczymy jako \(x\), to objętość sześcianu wyniesie \(3x\). Możemy zatem zapisać, że:
$$x+3x=36cm^3 \\
4x=36cm^3 \\
x=9cm^3$$
To oznacza, że nasz sześcian ma objętość:
$$3x=3\cdot9cm^3=27cm^3$$
Objętość sześcianu obliczamy ze wzoru \(V=a^3\), a skoro ta objętość wynosi \(27cm^3\), to otrzymamy równanie:
$$V=a^3 \\
27cm^3=a^3 \\
a=3cm$$
To oznacza, że drugie zdanie jest prawdą.
Zadanie 11. (4pkt) Trójkąt przedstawiony na rysunku jest ścianą boczną ostrosłupa prawidłowego trójkątnego.
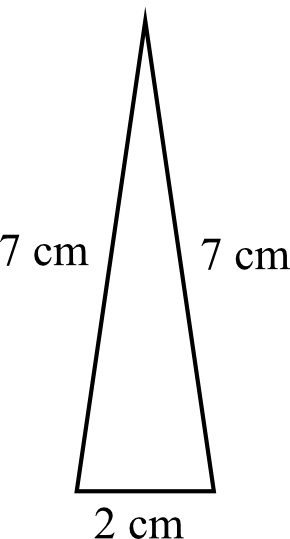
Oblicz pole powierzchni całkowitej tego ostrosłupa.
Odpowiedź
Pole powierzchni całkowitej tego ostrosłupa jest równe \(13\sqrt{3}cm^2\).
Wyjaśnienie:
Krok 1. Obliczenie pola podstawy.
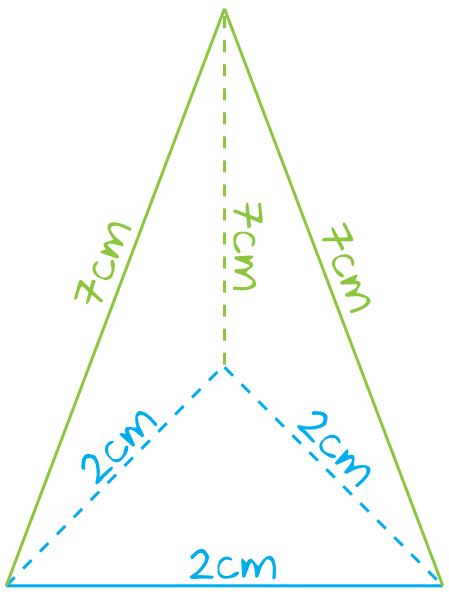
Wiemy, że ostrosłup jest ostrosłupem prawidłowym trójkątnym. To oznacza, że w podstawie musi znaleźć się trójkąt równoboczny. Z rysunku możemy od razu odczytać, że długość boku tego trójkąta znajdującego się w podstawie jest równa \(2cm\) (patrz rysunek), a skoro tak, to pole podstawy będzie równe:
$$P_{p}=\frac{a^2\sqrt{3}}{4} \\
P_{p}=\frac{2^2\sqrt{3}}{4} \\
P_{p}=\frac{4\sqrt{3}}{4} \\
P_{p}=\sqrt{3}[cm^2]$$
Krok 2. Obliczenie wysokości ściany bocznej.
Do obliczenia pola powierzchni całkowitej potrzebujemy znać jeszcze pola ściany bocznej. Aby ją obliczyć musimy poznać wysokość trójkąta i tu skorzystamy z Twierdzenia Pitagorasa oraz z własności trójkątów równoramiennych, która mówi nam że wysokość takiego trójkąta dzieli podstawę na dwie równe części.
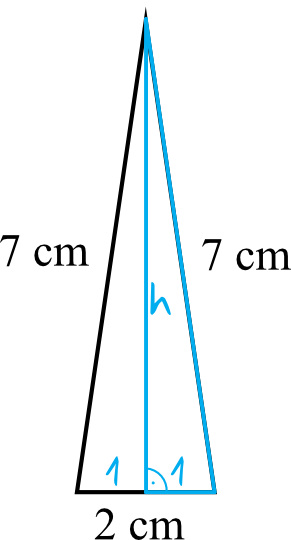
Z Twierdzenia Pitagorasa otrzymamy:
$$1^2+h^2=7^2 \\
1+h^2=49 \\
h^2=48 \\
h=\sqrt{48}=\sqrt{16\cdot3}=4\sqrt{3}[cm]$$
Krok 3. Obliczenie pola powierzchni pojedynczej ściany bocznej.
Wiemy już, że w ścianie bocznej znajduje się trójkąt o podstawie \(2cm\) oraz wysokości \(4\sqrt{3}cm\), zatem jego pole powierzchni będzie równe:
$$P_{b}=\frac{1}{2}\cdot2\cdot4\sqrt{3} \\
P_{b}=1\cdot4\sqrt{3} \\
P_{b}=4\sqrt{3}[cm^2]$$
Krok 4. Obliczenie pola powierzchni całkowitej.
Na pole powierzchni całkowitej składają się jedna podstawa oraz trzy ściany boczne, zatem:
$$P_{c}=P_{p}+3P_{b} \\
P_{c}=\sqrt{3}+3\cdot4\sqrt{3} \\
P_{c}=\sqrt{3}+12\sqrt{3} \\
P_{c}=13\sqrt{3}[cm^2]$$
Wyjaśnienie punktacji:
Przyznaj sobie:
0 pkt
• Gdy brakuje jakiegokolwiek postępu prowadzącego do rozwiązania zadania.
1 pkt
• Gdy obliczysz wysokość ściany bocznej (Krok 2.).
LUB
• Gdy obliczysz wysokość trójkąta znajdującego się w podstawie (\(h=\sqrt{3}\)).
2 pkt
• Gdy obliczysz pole podstawy (Krok 1.).
LUB
• Gdy obliczysz pole ściany bocznej (Krok 3.).
3 pkt
• Gdy obliczysz pole podstawy (Krok 1.) oraz pole ściany bocznej (Krok 3.)
4 pkt
• Gdy otrzymasz oczekiwany wynik.
Zadanie 12. (3pkt) Podstawą ostrosłupa o wysokości \(H\) jest kwadrat. Na rysunku przedstawiono siatkę i podano długości niektórych krawędzi tego ostrosłupa.
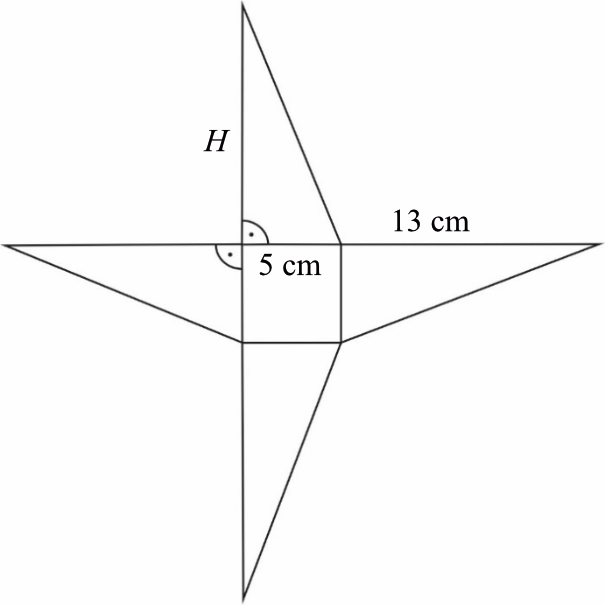
Oblicz objętość tego ostrosłupa.
Wyjaśnienie:
Krok 1. Sporządzenie rysunku pomocniczego.
Zadanie już na samym początku skrywa sporą pułapkę. Wbrew pozorom wysokość górnego trójkąta naszej siatki (czyli jednocześnie wysokość całej bryły) nie będzie mieć długości równej \(13cm\). Długość równą \(13cm\) będzie mieć przeciwprostokątna tego górnego trójkąta prostokątnego, bo tylko wtedy siatka da się złożyć w ostrosłup:
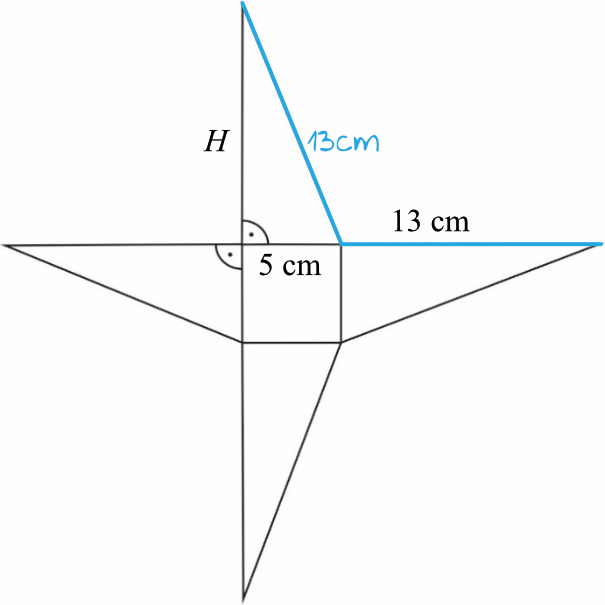
Krok 2. Obliczenie wysokości ostrosłupa.
Spójrzmy na górny trójkąt prostokątny w naszej siatce. Korzystając z Twierdzenia Pitagorasa możemy zapisać, że:
$$5^2+H^2=13^2 \\
25+h^2=169 \\
H^2=144 \\
H=12 \quad\lor\quad H=-12$$
Ujemny wynik oczywiście odrzucamy, bo wysokość ostrosłupa musi mieć dodatnią długość, zatem zostaje nam \(H=12cm\).
Krok 3. Obliczenie pola powierzchni podstawy.
W podstawie mamy kwadrat o boku \(5cm\), zatem pole powierzchni podstawy będzie równe:
$$P_{p}=a^2 \\
P_{p}=5^2 \\
P_{p}=25[cm^2]$$
Krok 4. Obliczenie objętości ostrosłupa.
Znamy już pole podstawy \(P_{p}=25cm^2\), wiemy też że wysokość bryły wynosi \(H=12cm\), zatem objętość będzie równa:
$$V=\frac{1}{3}P_{p}\cdot H \\
V=\frac{1}{3}\cdot25\cdot12 \\
V=100[cm^3]$$
Wspaniała strona można się wiele nauczyć. Pozdrawiam szkołę w Majdanie Nepryskim.
Super zadanie, wiele się nauczyłam
W zad.6 podstawową może być też romb, bo ma wszystkie boki równe, czyli jest czworokątem foremnym.
Romb nie jest czworokątem foremnym, bo nie ma kątów o jednakowej mierze ;) Jedynym czworokątem foremnym jest kwadrat.
Dlaczego w zadaniu siódmym nie oblicza się dołu dachu?
Hmmm, bo powierzchnia dachu to tylko powierzchnia ścian bocznych tego ostrosłupa ;) Jak układamy dachówkę na dachu, to też nie układamy jej „na dole” :)
W zadaniu 7 w wyjaśnieniu w kroku drugim jest napisane, że jest prostokąt. Ale wszystkie boki mają 8m więc jakim cudem uważasz, że jest gdzieś na drugim domie prostokąt?
Ale tam przecież wyliczam dach, a nie ścianę ;) Płaszczyzna dachu jest prostokątem o bokach 8 oraz x (i ten x musimy teraz wyznaczyć)
Super strona do nauki matematyki. Szkoła w Majdanie Nepryskim jest super :D
fajne fajne dzięki coś wiem
fajne stronka polecam
Świetna strona do nauki.
ciekawe zadania i fajnie że są wyjaśnienia
Super zadania pomogły mi zrozumieć
Dużo się nauczyłem lecz lekko trudne, to jest już większy poziom