Tangens to stosunek długości przyprostokątnej leżącej naprzeciw kąta \(α\) do długości przyprostokątnej leżącej przy kącie \(α\).
$$tgα=\frac{\text{dł. przyprostokątnej naprzeciw kąta α}}{\text{dł. przyprostokątnej przy kącie α}}$$
Dodatkowo możemy zapisać, że:
$$tgα=\frac{sinα}{cosα}$$
Zbiorem wartości tangensa jest zbiór liczb rzeczywistych. Warto też pamiętać, że dla kątów ostrych tangens przyjmuje wartości dodatnie.
Wykres funkcji tangens wygląda następująco:
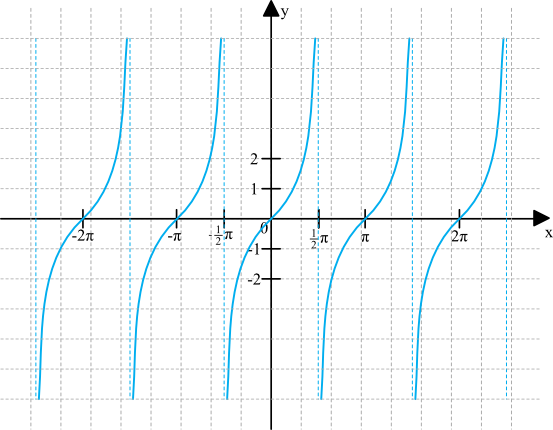
Dziedzina: \(x\in\mathbb{R}\backslash\{\frac{π}{2}+kπ\}\), gdzie \(k\in\mathbb{C}\)
Zbiór wartości: \(y\in\mathbb{R}\)
Miejsce zerowe: \(x_{0}=kπ\), gdzie \(k\in\mathbb{C}\)
Monotoniczność:
Funkcja rośnie w przedziałach \((-\frac{π}{2}+kπ; \frac{π}{2}+kπ)\), gdzie \(k\in\mathbb{C}\)
Okresowość: funkcja jest okresowa, okres podstawowy \(T=π\)
Parzystość: funkcja nieparzysta
Różnowartościowość: funkcja nie jest różnowartościowa
