W trójkącie równoramiennym \(ABC\) dane jest \(|AC|=|BC|=7\) oraz \(|AB|=12\). Wysokość opuszczona z wierzchołka \(C\) jest równa:
\(\sqrt{13}\)
\(\sqrt{5}\)
\(1\)
\(5\)
Rozwiązanie:
Krok 1. Sporządzenie rysunku poglądowego.
Z własności trójkąta równoramiennego wiemy, że jego wysokość dzieli podstawę na dwie równe części. Stąd też powstaną nam odcinki \(|AD|=|DB|=6\) (patrz rysunek)
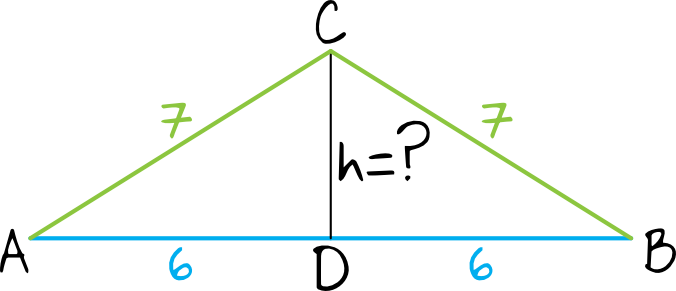
Krok 2. Obliczenie wysokości trójkąta.
Skorzystamy z Twierdzenia Pitagorasa.
$$|DB|^2+|CD|^2=|BC|^2 \\
6^2+|CD|^2=7^2 \\
36+|CD|^2=49 \\
|CD|^2=13 \\
|CD|=\sqrt{13}$$
Odpowiedź:
A. \(\sqrt{13}\)

