Styczna do okręgu to prosta, która ma z okręgiem tylko jeden wspólny punkt. Na tej lekcji dowiemy się jakie są podstawowe własności takich stycznych i z jakimi zadaniami możemy się spotkać w tym temacie.
Prosta i okrąg
Jeśli narysujemy okrąg i jakąś dowolną prostą, to możemy spotkać się z trzema różnymi sytuacjami:
· prosta może przechodzić przez okrąg, wtedy prosta i okrąg mają dwa punkty wspólne,
· prosta może przechodzić obok okręgu, wtedy prosta i okrąg nie mają punktów wspólnych,
· prosta może stykać się z okręgiem, wtedy prosta i okrąg mają jeden punkt wspólny.
Na rysunku wyglądałoby to w ten sposób:

Nas na tej lekcji interesuje ten ostatni przypadek. Jeśli prosta „styka się” z okręgiem w jednym punkcie to mówimy, że jest to styczna do okręgu. Punkt w którym „stykają się” prosta z okręgiem nazywamy punktem styczności. Oczywiście do okręgu możemy przyporządkować nieskończenie wiele różnych stycznych – będą miały one po prostu różne punkty styczności.
Styczna do okręgu i promień okręgu
Jeżeli od środka okręgu do punktu styczności poprowadzimy promień okręgu, to okazuje się, że ten promień będzie zawsze prostopadły względem stycznej do okręgu:
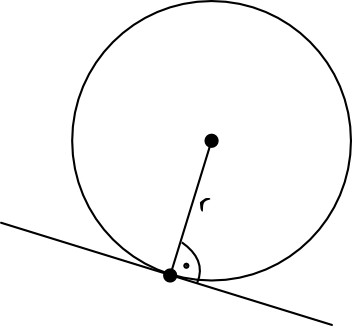
Jest to bardzo ważna własność, którą często będziemy wykorzystywać w tym temacie.
Przecięcie się dwóch stycznych
Jeżeli do danego okręgu poprowadzimy dwie styczne, które przetną się w jednym punkcie \(P\), to okazuje się, że odcinki łączące punkty styczności z punktem \(P\) będą miały tą samą długość.
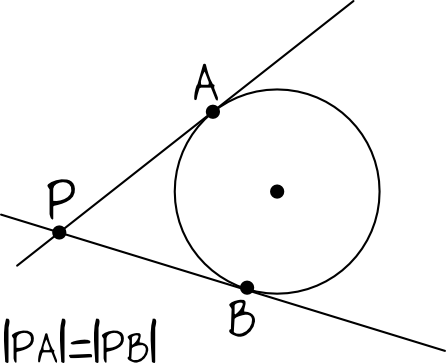
Sprawdźmy zatem jak wiedza na temat stycznych może być wykorzystywana w przykładowych zadaniach.
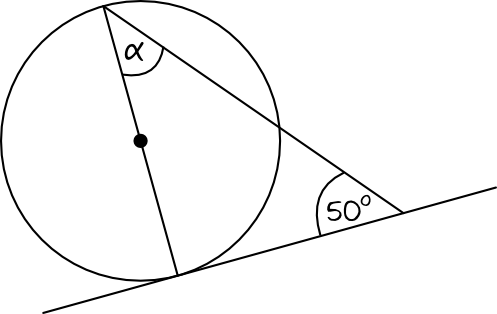
Rozwiązanie:
Skorzystamy tutaj z kluczowej własności stycznych do okręgu. Promień łączący środek okręgu wraz z punktem styczności jest zawsze prostopadły do stycznej. Tym samym jeden z boków (który pokrywa się ze średnicą okręgu), będzie prostopadły do naszej stycznej. To prowadzi nas do wniosku, że powstały na rysunku trójkąt jest prostokątny. Skoro tak, to znamy już miary dwóch kątów w tym trójkącie, czyli \(90°\) oraz \(50°\). To oznacza, że trzeci kąt oznaczony jako \(\alpha\), będzie miał miarę:
$$\alpha=180°-90°-50°=40°$$
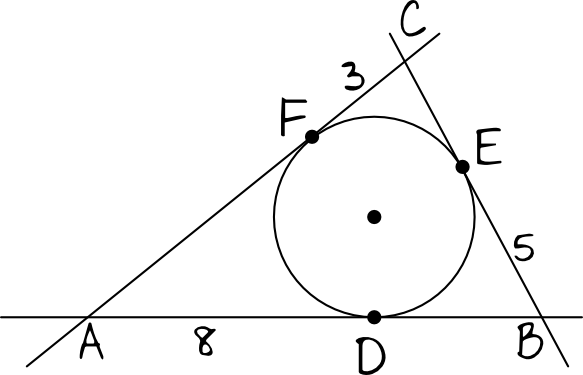
Rozwiązanie:
Zwróć uwagę, że boki trójkąta opisanego na okręgu są tak naprawdę stycznymi do okręgu, które się wzajemnie przecinają. Ta obserwacja pozwoli nam na skorzystanie z własności związanych z przecięciem się stycznych. Wiemy, że odcinki łączące punkty styczności z miejscami przecięcia się stycznych (które w naszym przypadku są wierzchołkami trójkąta) będą mieć jednakowe długości. Skoro tak, to powstanie nam taka oto sytuacja:

To oznacza, że obwód tego trójkąta jest równy:
$$Obw=8+5+5+3+3+8=32$$
Twierdzenie o kącie między styczną a cięciwą
W szkole średniej będziemy mówić o jeszcze jednej własności stycznych, którą nazywamy twierdzeniem o kącie między styczną a cięciwą. Więcej informacji o tym twierdzeniu znajdziesz tutaj:
Zobacz także:
