Styczna do okręgu ma kilka ciekawych własności, które wykorzystujemy w zadaniach z okręgami, a jedną z nich jest twierdzenie o kącie między styczną a cięciwą. Omówmy zatem to twierdzenie i pokażmy sobie jak jest ono wykorzystywane w praktyce.
Twierdzenie o kącie między styczną a cięciwą
Jeżeli od punktu styczności prostej z okręgiem poprowadzimy cięciwę okręgu, to kąt ostry między cięciwą okręgu a styczną okręgu jest równy kątowi wpisanemu w okrąg, który jest oparty na tej cięciwie.
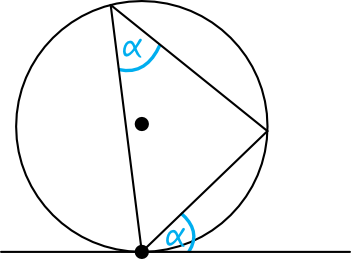
Spójrzmy na taki oto przykład:
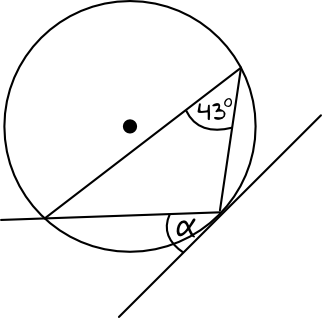
Rozwiązanie:
Kąt o mierze \(43°\) jest oparty na cięciwie, która to cięciwa tworzy ze styczną okręgu nasz poszukiwany kąt \(\alpha\). Jest to więc klasyczna sytuacja w której wykorzystamy twierdzenie o kącie między styczną a cięciwą – wynika z niego, że te dwa kąty będą miały jednakową miarę, stąd też \(\alpha=43°\).
Zadania związane z wykorzystaniem twierdzenia o kącie między styczną a cięciwą bardzo często związane są także z własnościami kątów wpisanych i środkowych. Jeśli chcesz je sobie powtórzyć, to wiedzę na ten temat znajdziesz tutaj:
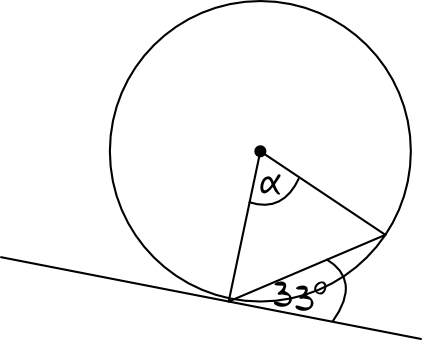
Rozwiązanie:
Tym razem na cięciwie mamy oparty kąt środkowy, a nie wpisany. Teoretycznie więc nie możemy skorzystać z poznanego przed chwilą twierdzenia, bo ono dotyczy kątów wpisanych, które opierają się na tej cięciwie. Spróbujmy jednak dorysować kąt wpisany, który opiera się na tej samej cięciwie/łuku co nasz kąt środkowy. Zgodnie z poznanym twierdzeniem o kącie między styczną a cięciwą, miara takiego kąta wpisanego będzie równa \(33°\), czyli powstanie nam taka oto sytuacja:
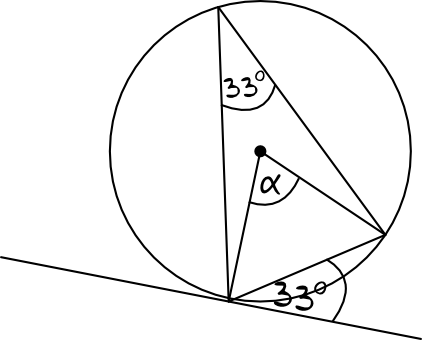
Teraz sprawa jest już prosta, ponieważ wystarczy skorzystać z własności kątów środkowych – wiemy, że kąt środkowy oparty na tym samym łuku co kąt wpisany będzie miał miarę dwa razy większą, stąd też:
$$\alpha=2\cdot33°=66°$$
Zobacz także:
