Na tej lekcji powiemy sobie jak mogą być położone względem siebie dwa okręgi i jakie to niesie ze sobą konsekwencje. Szczególną uwagę poświęcimy sytuacji, w której okręgi są styczne względem siebie.
Wzajemne położenie dwóch okręgów
Dwa okręgi mogą być położone względem siebie w następujący sposób:
1. Okręgi rozłączne
Dwa okręgi mogą nie mieć punktów wspólnych. Stanie się tak, gdy narysujemy jeden okrąg obok drugiego lub też gdy mniejszy okrąg znajdzie się w całości wewnątrz większego okręgu. Takie okręgi nazywamy rozłącznymi:
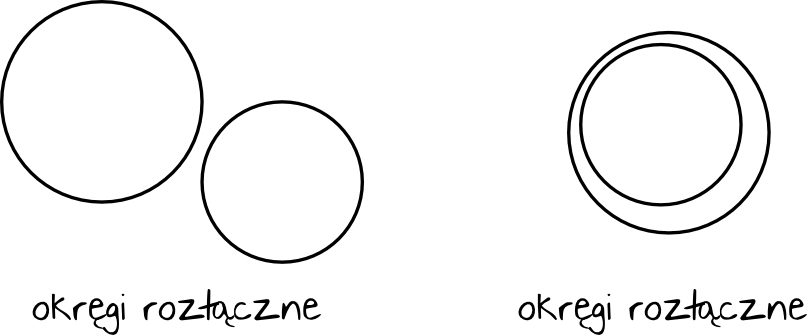
2. Okręgi przecinające się
Dwa okręgi mogą się przeciąć i jeśli tak się stanie, to będą miały one dwa punkty wspólne:
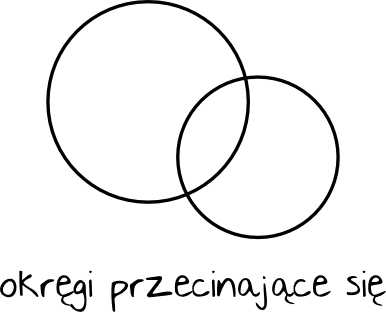
3. Okręgi styczne zewnętrznie i wewnętrznie
Dwa okręgi mogą też się ze sobą stykać, co sprawi, że będą miały tylko jeden wspólny punkt. Tu wyróżniamy dwie kluczowe sytuacje – okręgi mogą być styczne zewnętrznie lub też wewnętrznie.
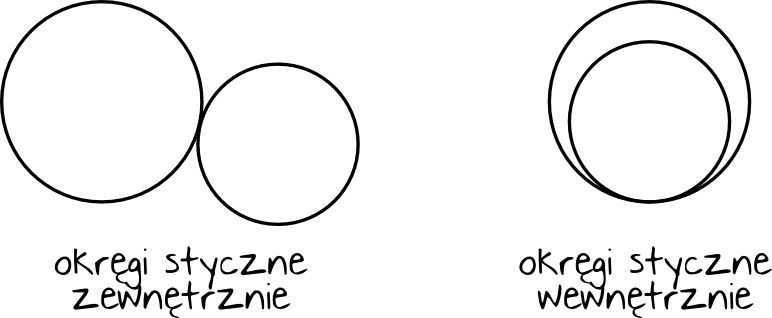
Odległość między środkami okręgów
Na lekcjach matematyki będziemy zajmować się nie tylko określaniem wzajemnych położeń danych okręgów (czyli na podstawie różnych informacji będziemy analizować, czy np. okręgi się przecinają), ale czeka nas także wyliczanie poszczególnych miar, zwłaszcza gdy będziemy mieć okręgi styczne. Tu bardzo pomocna będzie następująca obserwacja zachodząca w okręgach stycznych:
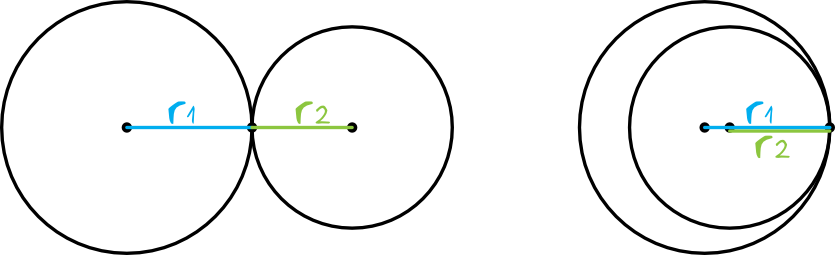
Widzimy wyraźnie, że:
· gdy okręgi są styczne zewnętrznie, to odległość między środkami okręgów jest równa sumie długości jednego i drugiego promienia,
· gdy okręgi są styczne wewnętrznie, to odległość między środkami okręgów jest równa różnicy długości jednego i drugiego promienia.
Pokażmy to sobie na konkretnych przykładach:
Rozwiązanie:
Dla lepszego zobrazowania, możemy zrobić sobie rysunek pomocniczy:
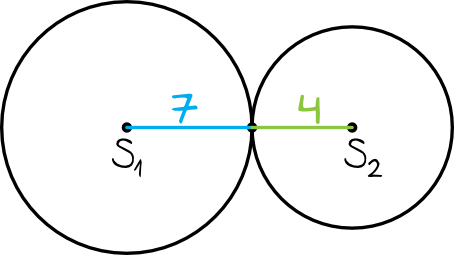
Z rysunku wynika wprost, że odległość między środkami okręgów będzie równa sumie długości promieni jednego i drugiego okręgu, zatem:
$$S_{1}S_{2}=4+7=11$$
Rozwiązanie:
Tym razem okręgi są styczne wewnętrznie, czyli odległość między środkami tych okręgów będzie równa różnicy długości promieni. Pewnym urozmaiceniem w tym zadaniu jest fakt, że nie znamy promieni naszych okręgów, ale obliczymy je w bardzo prosty sposób, korzystając ze wzoru na obwód okręgu, który przyjmuje postać \(Obw=2\pi r\). Obwód pierwszego okręgu wynosi \(6\pi\), zatem podstawiając tę informację do wzoru wyjdzie nam, że promień tego okręgu ma długość:
$$6\pi=2\pi r \\
r=3$$
I tak samo zrobimy z drugim okręgiem, którego obwód jest równy \(10\pi\), zatem:
$$10\pi=2\pi r \\
r=5$$
Nasze okręgi styczne wewnętrznie, więc sytuacja wygląda mniej więcej w ten sposób:
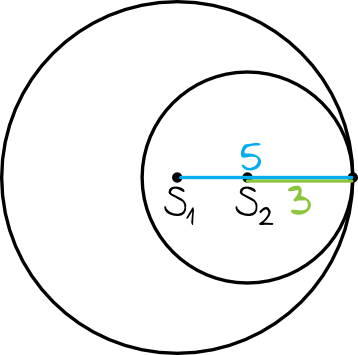
W takim razie odległość między środkami okręgów będzie równa:
$$S_{1}S_{2}=5-3=2$$
Oczywiście zadania nie muszą się opierać tylko na okręgach stycznych. Spójrzmy na takie oto zadanie:
Rozwiązanie:
Zadanie jest o tyle ciekawe, że w sumie nie wymaga od nas żadnych obliczeń. Pomocny będzie za to dobry rysunek. Rysujemy duży okrąg i dorysowujemy mniejszy w taki sposób, by przechodził on przez środek tego większego:
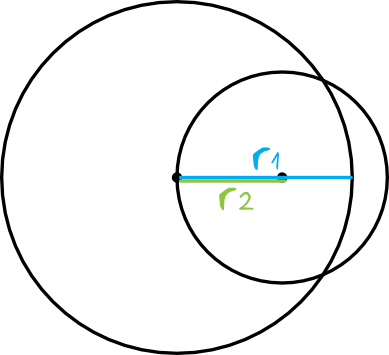
Widzimy więc, że poszukiwana odległość między środkami okręgów jest równa promieniowi mniejszego okręgu. Musimy jeszcze uważać tylko na pułapkę z treści zadania, ponieważ w zadaniu mamy podane długości średnic, a nie promieni. Wiemy, że promień jest dwa razy mniejszy od średnicy, zatem promień mniejszego okręgu będzie miał długość:
$$r=12:2=6$$
Odległość między środkami tych okręgów wynosi więc \(6\).
Zobacz także:
