Objętość stożka możemy obliczyć korzystając z następującego wzoru:
$$V=\frac{1}{3}P_{p}\cdot H$$
gdzie:
\(V\) – objętość stożka
\(P_{p}\) – pole podstawy stożka
\(H\) – wysokość stożka
Z racji tego, iż w podstawie znajduje się zawsze koło, którego pole powierzchni wyliczamy ze wzoru \(P=πr^2\), to możemy też zapisać, że:
$$V=\frac{1}{3}πr^2\cdot H$$
gdzie:
\(V\) – objętość stożka
\(r\) – promień podstawy stożka
\(H\) – wysokość stożka
Spójrzmy teraz na przykładowe zadania w których wykorzystujemy wzór na objętość stożka.
Korzystając ze wzoru na objętość stożka możemy zapisać, że:
$$V=\frac{1}{3}πr^2\cdot H \\
V=\frac{1}{3}π\cdot6^2\cdot4 \\
V=\frac{1}{3}π\cdot36\cdot4 \\
V=12π\cdot4 \\
V=48π$$
Krok 1. Obliczenie długości promienia podstawy.
Wiemy, że w podstawie znajduje się koło o obwodzie \(4π\). Obwód koła obliczamy ze wzoru \(2πr\), zatem:
$$Obw=4π \\
2πr=4π \quad\bigg/:π \\
2r=4 \\
r=2$$
Krok 2. Obliczenie wysokości stożka.
Wiemy, że stożek ma objętość \(V=12π\). Obliczyliśmy przed chwilą, że promień podstawy ma długość \(r=2\). W związku z tym:
$$V=\frac{1}{3}πr^2\cdot H \\
12π=\frac{1}{3}π\cdot2^2\cdot H \quad\bigg/:π \\
12=\frac{1}{3}\cdot4\cdot H \quad\bigg/\cdot3 \\
4H=36 \\
H=9$$
Krok 1. Sporządzenie rysunku pomocniczego.
Narysujmy sobie przykładowy stożek, zaznaczając na nim dane z treści zadania:
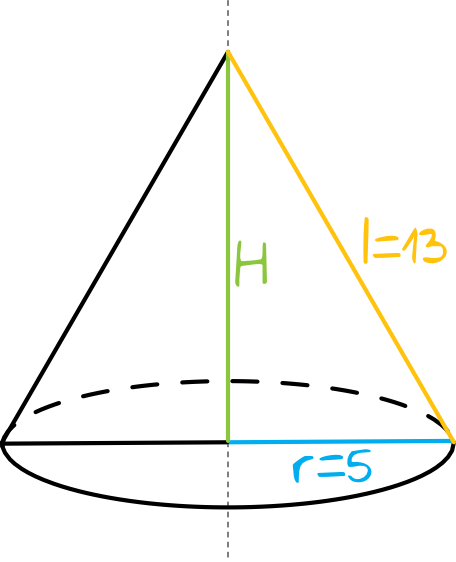
Krok 2. Obliczenie wysokości stożka.
Spójrzmy na trójkąt prostokątny, który utworzyły nam: promień podstawy, wysokość stożka oraz tworząca stożka. Znamy długości dwóch boków tego trójkąta, czyli \(r=5\) oraz \(l=13\), zatem korzystając z Twierdzenia Pitagorasa możemy zapisać, że:
$$5^2+H^2=13^2 \\
25+H^2=169 \\
H^2=144 \\
H=12 \quad\lor\quad H=-12$$
Wartość ujemną oczywiście odrzucamy, bo wysokość musi być dodatnia. Zostaje nam więc \(H=12\).
Krok 3. Obliczenie objętości stożka.
Znamy już wszystkie potrzebne miary, bowiem wiemy że \(r=5\) oraz \(H=12\), zatem:
$$V=\frac{1}{3}πr^2\cdot H \\
V=\frac{1}{3}π\cdot5^2\cdot12 \\
V=\frac{1}{3}π\cdot25\cdot12 \\
V=4π\cdot25 \\
V=100π$$
